Вариант шестой Контрольная работа № 1
Задание № 1
Дан определитель. Требуется: 1) вычислить определитель, разложив его по какой-либо строке (или столбце); 2) вычислить определитель, получив предварительно нули в какой-либо строке (или столбце).
Задание № 2
Дана система линейных уравнений. Требуется: 1) найти ее решение, используя правило Крамера; 2) записать систему в матричной форме и решить ее с помощью обратной матрицы; 3) решить систему методом Гаусса.
Задание № 3
Даны точки А1, А2, А3, А4. Постройте пирамиду А1А2А3А4. Определите:
а) длину ребра А1А2;
б) уравнение прямой А1А4;
в) написать уравнение плоскости А1А2А3;
г) объем тетраэдра;
д) площадь грани А1А2А3;
е) длину высоты, опущенной из точки А4 на грань А1А2А3;
ж) уравнение высоты, опущенной из точки А4 на грань А1А2А3;
з) косинус угла между ребрами А1А2 и А1А3;
и) угол между прямой А1А4 и плоскостью А1А2А3.
A1(0,0,1), А2(2,3,4), А3(6,1,2), А4(3,7,2).
Задание № 4
Приведите уравнение кривой второго порядка к каноническому виду и постройте ее. Укажите координаты вершин, фокусов. Напишите уравнение директрисы и асимптот, если они есть. Вычислите эксцентриситет кривой.
9x2 - 4y2 – 18x - 16y - 7 = 0
Задание № 5
Вычислите пределы функций.
Задание № 6
Вычислите производную.
а)
в)
б)
Задание № 7
Найдите наибольшее и наименьшее значения функции на заданном отрезке.
Задание № 8
Вычислите вторую производную заданной функции.
Задание № 9
Проведите полное исследование заданной функции и постройте ее график.
Контрольная работа № 2
Задание № 1
Найдите неопределенные интегралы.
Задание № 2
Найдите неопределенные интегралы.
Задание № 3
Вычислите определенные интегралы.
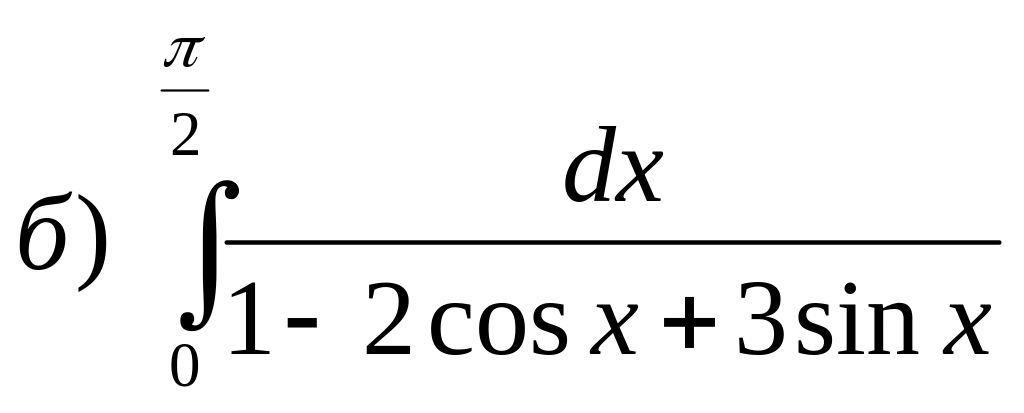
Задание № 4
Вычислите площадь фигуры, ограниченной линиями:
Задание № 5
Вычислите длину дуги кривой.
Задание № 6
Вычислите несобственные интегралы или исследуйте их на сходимость.
Задание № 7
Вычислите двойные интегралы.
Задание № 8
Вычислите криволинейный интеграл.
от точки (0;1) до точки (1; a)
Задание № 9
Вычислите тройной интеграл, если область V ограничена указанными поверхностями:
Вариант седьмой Контрольная работа № 1
Задание № 1
Дан определитель. Требуется: 1) вычислить определитель, разложив его по какой-либо строке (или столбце); 2) вычислить определитель, получив предварительно нули в какой-либо строке (или столбце).
Задание № 2
Дана система линейных уравнений. Требуется: 1) найти ее решение, используя правило Крамера; 2) записать систему в матричной форме и решить ее с помощью обратной матрицы; 3) решить систему методом Гаусса.
Задание № 3
Даны точки А1, А2, А3, А4. Постройте пирамиду А1А2А3А4. Определите:
а) длину ребра А1А2;
б) уравнение прямой А1А4;
в) написать уравнение плоскости А1А2А3;
г) объем тетраэдра;
д) площадь грани А1А2А3;
е) длину высоты, опущенной из точки А4 на грань А1А2А3;
ж) уравнение высоты, опущенной из точки А4 на грань А1А2А3;
з) косинус угла между ребрами А1А2 и А1А3;
и) угол между прямой А1А4 и плоскостью А1А2А3.
A1(1;5;-7), A2(-3;6;3), A3(-2;7;3), A4(-4;8;-12)
Задание № 4
Приведите уравнение кривой второго порядка к каноническому виду и постройте ее. Укажите координаты вершин, фокусов. Напишите уравнение директрисы и асимптот, если они есть. Вычислите эксцентриситет кривой.
9x2 - 16y2 – 36x - 64y - 172 = 0
Задание № 5
Вычислите пределы функций.
Задание № 6
Вычислите производную.
а)
в)
б)
Задание № 7
Найдите наибольшее и наименьшее значения функции на заданном отрезке.
Задание № 8
Вычислите вторую производную заданной функции.
Задание № 9
Проведите полное исследование заданной функции и постройте ее график.
