1.8. Произвести перерасчет размеров, допусков и отклонений методами полной взаимозаменяемости и теоретико-вероятностным: 4.2-5(квалитет -1).

Перещитаем размеры от заданной базы Б2 (Рис.13).

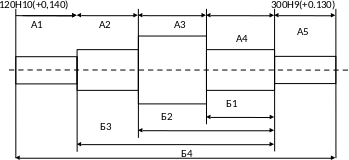
Рис.13 схема размерной цепи.

Метод полной взаимозаменяемости

Первая размерная цепь.

А₃=А_Δ; Б₁=А₄; А_Δ=Б₂-Б₁. Откуда Б₂=А_Δ+Б₂=50+20=70мм;

ТА_Δ=ТБ₂+ТБ₁; ТБ₂=ТА_Δ-ТБ­₁=0.021-(-0.038)=0.059мм.

Вторая размерная цепь

А₂=А_Δ; А_Δ=Б₃-Б₂. Откуда Б₃=А₂+Б₂=130+70=200мм;

ТА_Δ=ТБ₃+ТБ₂; ТБ₃=ТА₂-ТБ­₂=0.025-0.005=0.02мм.

Третья размерная цепь.

А₁=А_Δ; А_Δ=Б₄-Б₃. Откуда Б₄=А₁+Б₃=120+200=320мм;

ТА_Δ=ТБ₄+ТБ₃; ТБ₄=ТА₃-ТБ₃=0.140-0.020=0.120мм.

Рассчитаем отклонений: Es(A_Δ)=∑Es(A_j)- ∑Ei(A_j);

Ei(A_j)= Ei(A_j)- ∑Es(A_j);

Первая размерная цепь

Es(A_Δ)= откуда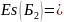 Es(A₃) =0+0.016=0.016мм;

Ei(A_Δ)= Ei(Б₂)- Es(Б₁); откудаEi(Б₂)= Ei(A₃)+ Es(Б₁)=0.021+(-0.016)=0,005мм;

Б₂=

Вторая разветвленная цепь

Es(A_Δ)= откуда Es(A₂) =0+0.005=0.005мм;

Ei(A_Δ)= Ei(Б₃)- Es(Б₂); откудаEi(Б₃)= Ei(A₂)+ Es(Б₂)=-0.025+0.005=-0.02мм;

Б₃=

Третья размерная цепь

Es(A_Δ)= откуда Es(A₃) =0.140+0.020=0.160мм;

Ei(A_Δ)= Ei(Б₄)- Es(Б₃); откудаEi(Б₄)= Ei(A₃)+ Es(Б₃)=0+0.020=0.020мм;

Б₄= .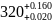

Теоретико-вероятностный метод.

Расчет допусков: A_Δ=∑Б_j-∑Б_j; TA_Δ=(∑Б_j²)^1/2.

Первая размерная цепь.

А₃=А_Δ; Б₁=А₄; А_Δ=Б₂-Б₁. Откуда Б₂=А_Δ+Б₁=50+20=70мм;

ТА_Δ=(ТБ₂²+ТБ₁²)^1/2; ТБ₂=(ТА₃²-ТБ­₂²)^1/2=(0.021²-(-0.038²)^1/2=0.043мм.

Вторая размерная цепь

А₂=А_Δ; А_Δ=Б₃-Б₂. Откуда Б₃=А₂+Б₂=130+70=200мм;

ТА_Δ=(ТБ₃²+ТБ₂²)^1/2; ТБ₃=(ТА₂²-ТБ­₂²)^1/2=(0.025²-0.005²)^1/2=0.0245мм.

Третья размерная цепь.

А₁=А_Δ; А_Δ=Б₄-Б₃. Откуда Б₄=А₃+Б₃=120+200=320мм;

ТА_Δ=(ТБ₃²+ТБ₄²); ТБ₄=(ТА₃²-ТБ₃²)^1/2=(0.140²-0.020²)^1/2=0.139мм.

Рассчитаем отклонений: Es(A_Δ)=∑Es(A_j)- ∑Ei(A_j);

Ei(A_j)= Ei(A_j)- ∑Es(A_j);Ращет допусков закончен.

Рассчитаем отклонения: Ес(A_Δ)=∑Ес(А_j)-∑Ес(А_j); Еs(A_j)=Ес(А_j)-TА_j/2;

Еi(A_j)=Ес(А_j)-TА_j/2; Ес(A_j)=(Еs(А_j)+Еi(А_j)/2);

Первая размерная цепь

Ec(Б₂)= ; Ec(A₃)=Ec(A_Δ)= =0;

Ec(A_Δ)=Ec(Б₂)-Ec(Б₁), откудаEc(Б₃)= Ec(A₃)+ Ec(Б₁)=0+ =0.0105мм;

=Ec(Б₁)+ТБ₂/2=0,0105+0,005/2=0,078мм;

=Ec(Б₁)-ТБ₂/2=0,0105-0,005/2=0,003мм;

Б₂=

Вторая разветвленная цепь

Ec(Б₃)= 0,0105; Ec(A₂)=Ec(A_Δ)= =0,07;

Ec(A_Δ)=Ec(Б₃)-Ec(Б₂), откудаEc(Б)= Ec(A₂)+ Ec(Б₂)= 0,07+ =0,0805мм;

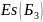=Ec(Б₄)+ТБ₃/2=0,0805+0,020/2=0.905мм;

=Ec(Б₄)-ТБ₃/2=0,0805-0,020/2=0.031мм;

Б₃= ;

Третья размерная цепь

Ec(Б₃)= 0,0805; Ec(A₂₁)=Ec(A_Δ)= =0,0125;

Ec(A_Δ)=Ec(Б₄)-Ec(Б₃), откудаEc(Б)= Ec(A)+ Ec(Б₃)= 0.0805+ =0,093мм;

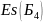=Ec(Б₅)+ТБ₄/2=0,093+0,005/2=0.049мм;

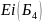=Ec(Б₅)-ТБ₄/2=0,093-0,005/2=0.044мм;

Б₄= ;

1.9. Определим допуски и придельные отклонения составляющих размеров методами полной взаимозаменяемости и теоретико-вероятностным:

4.1-5(А_Δ=А₁).

Дано: A_Δ=A₁, ТА_Δ=1,5мм, А₁=18мм, А₂=100мм,А₃=7мм,А₄=70мм,А₅=260мм,А₆=?,А₇=5мм.

Схема расчета цепи (Рис 14).

Рассчитаем размер звена А₆

А_Δ=∑А_j ∑А_j=(А₄+ А₃+ А₂+ А₆+ А₇)-( А₅+A)откуда А₆ =(А_Δ+ А₅)-(А₂+ А₃+ А₄+А₇)=20-40-6-90-16+200+20=48мм.

Метод полной взаимозаменяемости

Определим число единиц допусков по формуле а=(ТА_Δ-∑ТА_r)/∑i_j, где ∑ТА_r-сумма известных допусков.

У нас ∑ТА_r=0, тогда а=ТА_Δ/∑i_j; допуск замыкающего звена ТА_Δ=ES(А_Δ)- Ei(А_Δ)=0-1.8=1.8мм=1800мкм, ∑I_j-сумма единиц допусков составляющих звеньев. Выберемединицыдопусков:i₂=2,20мкм,i₃=0,73мкм,i₄=1,56мкм,i₅=2.9мкм,i₆=1.56мкм,i₇=1.08мкм.а=ТА_Δ/∑i_j=1800/(2,20+0.73+1.56+2.9+1.56+1.08)=1800/10.8=166.6мкм. Выберем ближайший 12^й квалитет с а=160. Вберем допуски всех звеньев, кроме замыкающего: ТА₂=0.35мм, ТА₃=0.3мм, ТА₄=0,25мм, ТА₅=0,45мм, ТА₆=0,25мм, ТА₇=0,18мм.

Проверим правильность выбора допусков.

∑ТА_j ∑ТА_Δ. (0.35+0.3+0.25+0.45+0.25+0.18) ТА_Δ,1.78  1.8

Условие выполняется. Теперь ТА_Δ=∑ТА_j=1.78 иА_Δ=1.8,

А_Δmax=20, А_Δmin=20-0,7=17,3мм;

А₂=90 0.35;А₃=6 0.15; А₄=40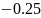 ; А₅=200^+0.45;А₆=48_-0.25; А₇=16 0,09;

Рассчитаем новые действительные отклонения замыкающего звена:

ES^’(А_Δ)= ES’(А_j)- Ei’(А_j)= 0.35+0.15+0+0+0.09-0=0,59мм;

EI^’(А_Δ)= Ei’(А_j)- ES’(А_j)=(0-0.15-0.25-0.25-0.09)-0.45=-1.19мм;

Наибольший придельный размер замыкающего звена

А_Δmax=A_Δ’+ ES’(А_Δ), откуда A_Δ’=А_Δmax-ES’(А_Δ)=20-0.59=19.41мм.

Новый замыкающий размер A_Δ= .

Замыкающее звено уменьшилось на  0,59, уменьшим на такое же значение звено А₂ получится А₂= . Расчет закончен.

Теоретико-вероятностный метод.

Определим число единиц допусков по формуле а=(ТА_Δ-∑ТА_r)/(∑i_j²)^1/2, где ∑ТА_r-сумма известных допусков.

У нас ∑ТА_r=0, тогда а=ТА_Δ/(∑i_j²)^1/2_j; допуск замыкающего звена

ТА_Δ=ES(А_Δ)- Ei(А_Δ)=0-1.8=1.8мм=1800мкм, ∑I_j-сумма единиц допусков составляющих звеньев. Выберемединицыдопусков:i₂=2,2мкм,i₃=0,73мкм,i₄=1.56мкм,i₅=2.9мкм,i₆=1.56мкм,i₇=1.08мкм.а=ТА_Δ/(∑i_j²)^1/2=1800/(2.2+0.73+1.56+2.9+1.56+1.08)=166.6мкм.

Выберем ближайший 11^й квалитет с а=100. Вберем допуски всех звеньев, кроме замыкающего: ТА₂=0.87мм, ТА₃=0.48мм, ТА₄=0.62мм, ТА₅=1.15мм, ТА₆=0.62мм, ТА₇=0.43мм.

Проверим правильность выбора допусков.

∑(ТА_j²)^1/2 ∑ТА_Δ. (0,87²+0.48²+0.62²+1.15²+0.62²+0.43²)^1/2 ТА_Δ,1.806  2 Условие выполняется.

А₂= ;А₃=6 0.48; А₄=40 0,62; А₇=16^+0,43; А₅=200_-1.15; А₆=48 0.62;

Рассчитаем новые действительные отклонения замыкающего звена:

Ec(А_j)=(ES(А_j)+Ei(А_j))/2; Ec(А₂)=0.435; Ec(А₃)=0; Ec(А₄)=0; Ec(А₅)=0,575;

Ec(А₆)=0; Ec(А₇)=0.215.

Ec^’(А_Δ)= ∑Ec^’(А_j)- ∑ec’(А_j)=0.435+0+0+0.215-0.575=0.075мм;

ES’(А_Δ)= Ec^’(А_Δ)-TA_Δ/2=0.075+0.09=0.975м.

Новый замыкающий размер A_Δ= .

Замыкающее звено уменьшилось на  0.975, уменьшим на такое же значение звено А₂ получится А₂= . Расчет закончен.