18.4.2. Процессы в области дрейфа

Рассмотрим теперь процессы, происходящие в области дрей­фа, куда приходят электроны из слоя умножения. При постоянст­ве скорости дрейфа электронов ток проводимости i(x,t) на рассто­янии х от слоя умножения равен току, протекающему в начале об­ласти дрейфа (т.е. току лавины), но в более ранний момент вре­мени (t - ), где – время пролета электронов от начала слоя дрейфа до сечения х. Если поместить начало координат на грани­це слоев умножения и дрейфа, то =х/. Следовательно,

В дальнейшем нас будет интересовать наведенный ток i(t), воз­никающий во внешней цепи при движении электронов в области дрейфа и называемый током дрейфа. Он численно равен току про­водимости i(x,t), усредненному по длине слоя дрейфа =–:

(18.11)

Заменив в (18.11) переменную интегрирования х на = t – x/ и подставив под знак интеграла выражение (18.10), найдем первую гармонику наведенного тока :

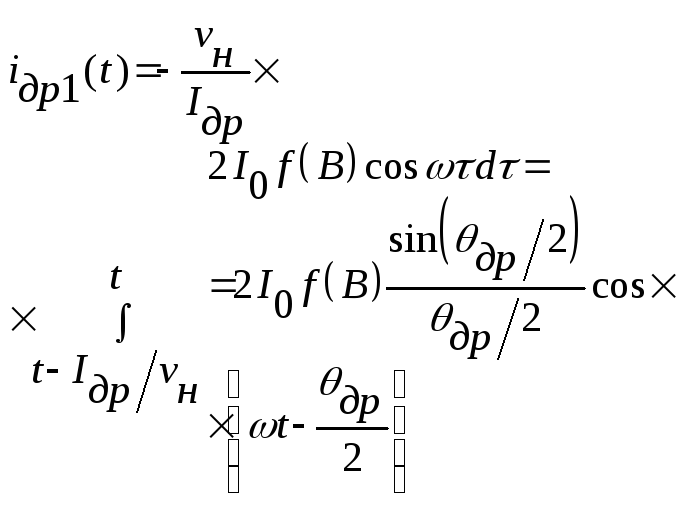(18.12)

где =/– угол пролета электронов в области дрейфа (см. рис. 18.7).

Согласно (18.12) ток дрейфа по сравнению с током лавиныимеет меньшую враз амплитуду и отстает по фазе на угол/2. Это обусловлено конечным временем пролета электронов в области дрейфа.

Ток лавины отстает от напряжения на слое умножения (t) и соответственно от напряжения на диоде u(t) на четверть периода. Поэтому результирующий сдвиг между наведенным током и СВЧ-напряжением (t) равен (/2 +/2). Тогда при=наведен­ный тококазывается в противофазе с напряжением (t), т.е. сопротивление ЛПД на частоте отрицательно.

18.4.3. Эквивалентная схема и высокочастотное сопротивление лпд

Для расчета высокочастотного сопротивления ЛПД по основной гармонике колебания воспользуемся эквивалентной схемой, пред­ложенной Ридом (рис. 18.10). Все токи и напряжения, показанные на этой схеме, являются гармоническими функциями времени, поэто­му их можно рассматривать в комплексной форме. Слой умножения здесь замещен генератором тока лавины с комплексной амплитудой и емкостью=(S/) ( – диэлектрическая проницаемость полупроводника). Соответственно область дрейфа замещена гене­ратором наведенного тока и ем­костью=(S/). Напряжение на диоде складывается из напря­жений, падающих на слоях умноже­ния и дрейфа: =+. Полный ток , протекающий во внешней цепи, не зависит от координаты и со­стоит из суммы тока проводимости и емкостного тока:

Пользуясь эквивалентной схе­мой (рис. 18.10) и уравнениями (18.8), (18.10) и (18.12), можно получить следующее выражение для высокочастотного сопротивления ЛПД:

(18.13)

где

(18.14)

(18.15)

С – емкость обедненного слоя дио­да; =– параметр, получивший названиелавинной ча­стоты; Ф(В)=2f(B)/B.

Согласно (18.14) и (18.15) актив­ное R и реактивное Х сопротивле­ния ЛПД зависят от нормированной амплитуды колебаний В через функ­цию Ф(В). График этой функции по­казан на рис. 18.9. На рис. 18.11 при­ведены зависимости R и СХ от В, рассчитанные по формулам (18.14) и (18.15) при /=0,6, = 0,64, С/= 4/5.

Согласно рис. 18.11,а отрица­тельное сопротивление R макси­мально в режиме слабого сигнала (при В0), с ростом амплитуды ко­лебаний оно монотонно уменьшается. Реактивное сопротивление Х определяется в основном «холодной» емкостью диодаС. Как видно из рис. 18.11,б, по ме­ре увеличения В разница меж­ду Х и емкостным сопротивле­нием –1/С уменьшается по абсолютной величине, сохра­няя отрицательный знак.

Из уравнения (1814) следу­ет, что активное сопротивление отрицательно при выполнении условия/Ф(B)<1. Физи­чески оно означает, что емкостный ток в слое умножения должен превышать ток проводимости 2f(B). Поскольку в порого­вом режиме (при В0) функция Ф(В) стремится к максимальному значению, равному единице (см. рис. 18.9), то записанное выше неравенство может выполняться только при >. Это означает, что генерация СВЧ-колебаний возможна лишь на частотах , превы­шающих лавинную частоту .

В соответствии с (18.14) и (18.15) активное R и реактивное Х сопротивления ЛПД зависят от частоты . На рис. 18.12 приведены зависимости малосигнальных значенийR и Х от . Зависимость от­рицательного сопротивленияR от определяется влиянием «пролетного» множителя (1 – соs)/ в (18.14), который обращается в нуль при = и достигает максимального значения при = 0,7. Частоту, при которой =. называют пролетной (): =/, где=/– время пролета в области дрейфапри скорости насыщения. Если диод предназначен для работы в диапазоне частот ..., то длина области дрейфа выбирает­ся обычно так, чтобы оптимальный угол пролета соответст­вовал бы средней частоте диапазона.