Глава 18 лавинно-пролетные диоды

18.1. Взаимодействие носителей заряда с кристаллической решеткой в сильном электрическом поле

В слабом электрическом поле (Е < 10³ В/см) энергия носителей заряда (электронов и дырок) сравнительно мала и достаточна лишь для возбуждения акустических колебаний кристаллической решетки (акустических фононов). Поэтому потери энергии при столкновениях с решеткой невелики и дрейфовая скорость носителей заряда рас­тет пропорционально напряженности электрического поля , где– подвижность носителей заряда является константой. В этом случае полупроводник ведет себя как линейный резистор, сопротив­ление которого не зависит от напряженности поля [см. § 2.2.2].

В сильном электрическом поле носители не успевают отда­вать решетке всю энергию, приобретаемую от поля за время сво­бодного пробега, в результате их средняя энергия увеличивается. Это обстоятельство позволяет говорить о разогреве носителей заряда и называть горячими те носители, энергия которых значи­тельно превышает среднюю тепловую энергию носителей в со­стоянии равновесия.

В сильных полях проявляются важные для рассматриваемых ниже полупроводниковых приборов эффекты. Один из них связан с нарушением линейной связи между дрейфовой скоростью носи­телей заряда и напряженностью электрического поляЕ. При Е > 10³ В/см энергия носителей становится достаточной для воз­буждения оптических колебаний решетки (оптических фононов). При этом потери энергии из-за столкновений с решеткой возрас­тают настолько, что рост дрейфовой скорости с увеличениемЕ сначала замедляется, а при Е > 10⁴ В/см прекращается совсем. Последнее эквивалентно уменьшению подвижности с ростомЕ.

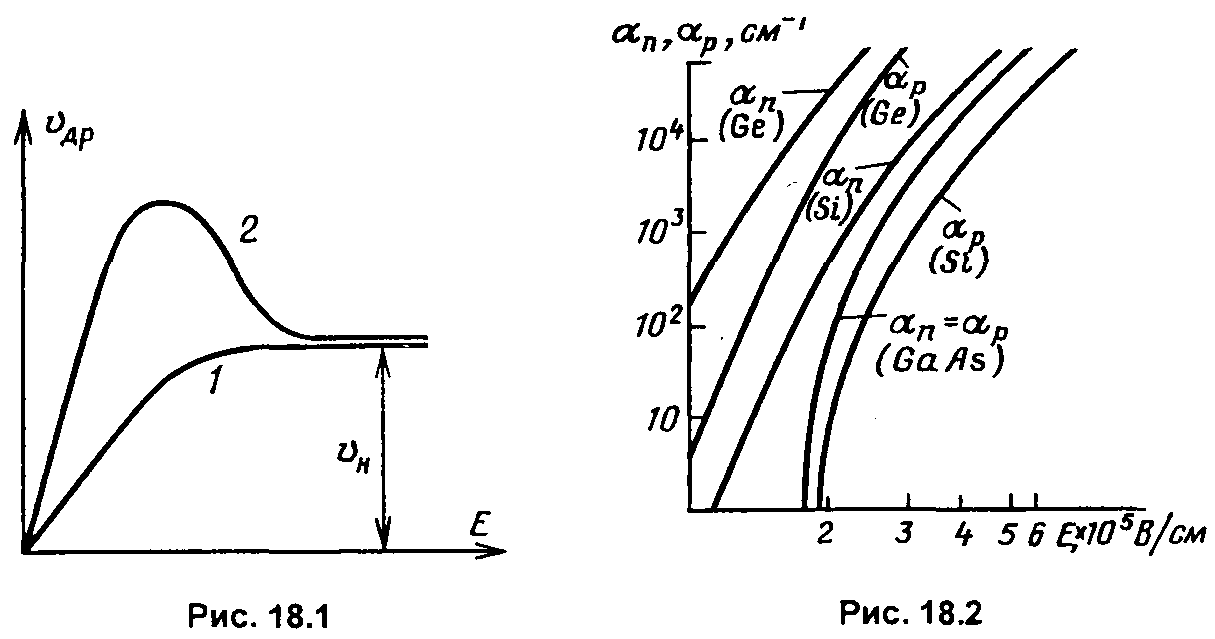
Это явление получило название насыщения дрейфовой ско­рости. Сказанное иллюстрирует рис. 18.1, на котором показана типичная зависимость (Е) (кривая1). Именно такая зависимость характерна для кремния и германия (материалов, использу­емых главным образом для изготовления приборов). Величина дрейфовой скорости насыщения обычно близка к 10⁷ см/с.

В некоторых материалах (арсенид галлия, фосфид индия) зави­симость (Е) более сложная: перед переходом к насыщению дрей­фовая скорость проходит через максимум (кривая 2). Эта особен­ность будет рассмотрена и использована в гл. 19.

В очень сильных полях проявляется еще один важный эффект – ударная ионизация атомов кристаллической решетки. Как уже отме­чалось в § 3.5.3, она происходит в тех случаях, когда энергия носите­лей заряда, сталкивающихся с решеткой, превышает энергию связи валентных электронов с атомами. При ионизации валентный элект­рон отрывается от атома и переходит в зону проводимости. При сла­бых и умеренных полях ударная ионизация практически отсутству­ет. Этот процесс становится существенным при достаточно боль­шой напряженности поля, превышающей 10⁵ В/см.

Процесс ионизации характеризуется коэффициентами удар­ной ионизации для электронов (если ионизирует электрон) и для дырок (если ионизирует дырка). Эти коэффициенты определя­ются как среднее число электронно-дырочных пар, генерируемых на единице пути (1 см) электроном или дыркой соответственно. Ко­эффициенты и сильно зависят от напряженности поля (изме­нениеЕ в 2 раза может приводить к изменению и на один-два порядка). Зависимости и от напряженности поля для герма­ния, кремния и арсенида галлия показаны на рис. 18.2. В теории ча­сто аппроксимируют эти зависимости следующим образом:

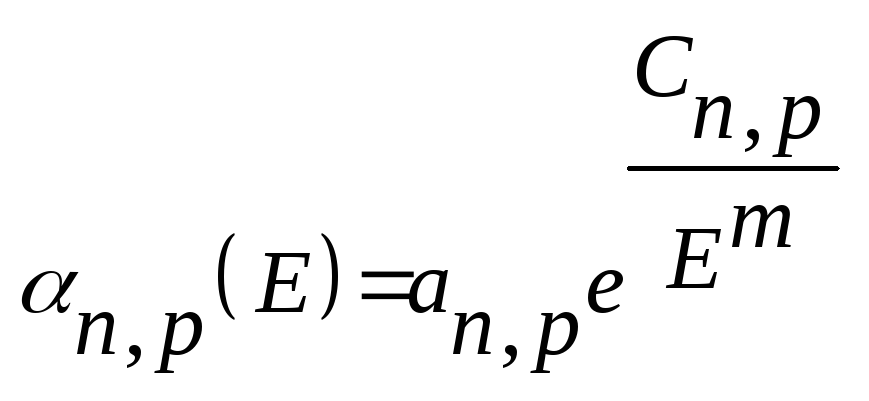(18.1)

где ,зависят от свойств материала и температуры;т = 1.. .2. Для арсенида галлия коэффициенты ионизации и примерно одинаковы, для кремния и германия они различаются. В дальней­шем для упрощения будем считать ==.

18.2. Статический режим работы ЛПД. Лавинный пробой p⁺-n-перехода

У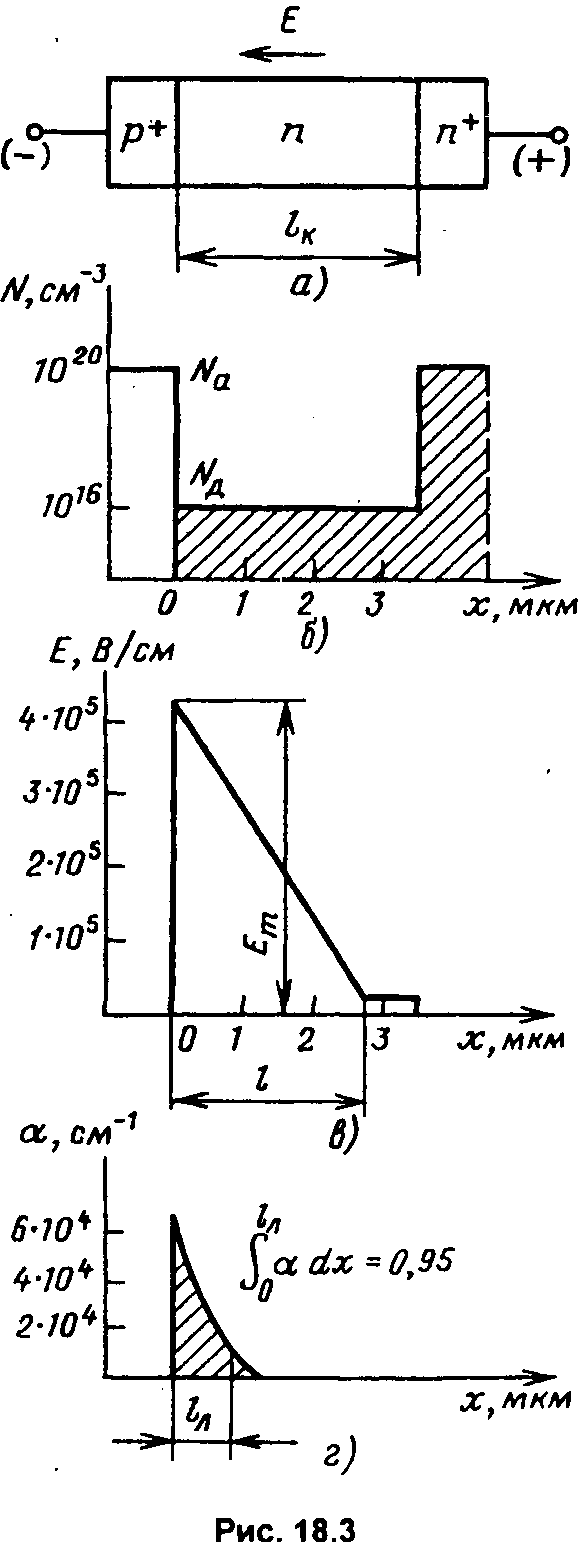дарная ионизация вызывает лавинное размножение носите­лей при напряженности электрического поляЕ, превышающей 10⁵ В/см. Реализовать такие поля в однородных полупроводниках (по крайней мере в непрерывном режиме) невозможно. Из-за нагрева током проводимости тепловой пробой произойдет раньше, чем начнется лавинное размножение носителей. Поэтому для созда­ния лавинных приборов используют барьерные переходы в режи­ме обратного включения. В обедненном слое перехода легко по­лучить поля порядка 10⁵ В/см без опасности теплового разруше­ния, поскольку обратный ток пе­рехода очень мал.

Рассмотрим типичную для лавинно-пролетных диодов структу­ру – резко несимметричный р⁺-n-переход (рис. 18.3,а) и про­анализируем его работу в стати­ческом режиме при обратном включении. Здесь же показаны распределения концентрации ле­гирующих примесей (18.3,б), на­пряженности электрического по­ля Е (18.3,в) и изменение коэф­фициента ударной ионизации по координатех (18.3,г). Цифры на осях характерны для ЛПД сан­тиметрового диапазона волн.

Поскольку легирующая при­месь распределена в n-области равномерно, поле пространст­венного заряда в соответствии с уравнением Пуассона спадает в переходе по линейному закону

где – толщина обед­ненного слоя;–относительная диэлектрическая проницаемость полупроводника и проницаемость вакуума,– концентрация донорной примеси в базе диода.

ЛПД сантиметрового диа­пазона волн для повышения надежности и долговечности толщина обедненного слоя I обычно меньше расстояния между контактамир⁺ и n⁺, т.е. диод не «проколот» (под проко­лом понимают распростране­ние поля пространственного заряда до контакта). Макси­мальная напряженность поля имеет место на границе р⁺-n-перехода. В сильнолеги­рованную р⁺-область поле пра­ктически не проникает.

Коэффициент ионизации, резко зависящий от напряженности поля, снижается при ее умень­шении очень быстро (рис. 18.3,г). Поэтому ионизация происходит в основном в узком слоеn-области, в котором Е близко к . Этот слой называется слоем умножения.

Рассмотрим теперь токи, протекающие в обедненнойn-области ЛПД (рис. 18.4). Напомним, что при обратном смещении ток че­рез переход обусловлен экстракцией неосновных носителей за­ряда. Электроны, экстрагированные из р⁺-области, создают на ле­вой границе перехода (х = 0) начальный ток , а дырки, экстраги­рованные из нейтрального участкаn-области, образуют на правой границе перехода (х = I) начальный ток (см. рис. 18.4). Именно эти носители заряда инициируют при определенном условии про­цесс лавинного размножения – возникновение новых пар носите­лей в результате ударной ионизации. При этом вновь образован­ные дырки дрейфуют налево, а число их увеличивается по мере приближения к границе с р⁺-областью. Электроны, напротив, дрейфуют направо, причем их количество возрастает по мере приближения к правой границе р⁺-n-перехода. Изменение элект­ронного и дырочного токов в переходе показано на рис. 18.4,б. Обратим внимание, что в статическом режиме полный ток через переход =+ не зависит от координаты.

Интенсивность процесса ударной ионизации характеризуется коэффициентом лавинного умножения М = /, который показывает, во сколько раз возрастает обратный ток перехода за счет ударной ионизации по сравнению с тепловым током =+ в формуле (3.40). Замена обозначения на общепринята для ЛПД.

При напряжении на диоде, равном пробивному , коэффициентМ стремится к бесконечности, т.е. ток через переход неограниченно нарастает. Это явление называют лавинным пробоем (см. § 3.5.3).

Ниже [см. формулу (18.7)] будет показано, что условие лавинно­го пробоя имеет вид

(18.2)

Физический смысл этого равенства состоит в следующем: для возникновения лавинного пробоя необходимо, чтобы каждый но­ситель, вошедший в переход, и каждая пара электрон-дырка, возникшая в переходе, порождали бы в среднем по одной элект­ронно-дырочной паре.

Используя (18.2) и зная распределение поля в обедненном слое Е(х) и зависимость (Е) (формула (18.1)), можно найти макси­мальное значение поля =Е(х=0) при пробое. Для GaAs и при ти­пичном значении концентрации донорной примеси = 10¹⁶ см ^-3 величина составляет примерно 4·10⁵ В/см. При этом длина обедненного слоя примерно равна 3 мкм.

Из рис. 18.3,г видно, что между слоем умножения, где в основ­ном происходит ударная ионизация, и остальной частью обеднен­ной области нет четкой границы. Обычно определяют длину слоя умножения из условия, чтобы внутри этого слоя (0<х <) генери­ровалось 90...95% электронно-дырочных пар. Величина, как правило, не превышает четверти длины обедненного слоя.

Участок обедненного слоя, ограниченный координатами х=и х=, называетсяслоем дрейфа, а его длина =–– длиной дрейфа. В слой дрейфа приходят электроны из слоя умножения и дрейфуют там с постоянной скоростью, равной скорости насыще­ния , поскольку почти во всей области дрейфа напряженность электрического поля Е больше, чем 10⁴ В/см. Заметим также, что дырки, возникающие при генерации пар в слое умножения, втяги­ваются полем в р⁺-область.

В заключение рассмотрим статическую характеристику ЛПД (рис. 18.5). При обратном смещении (U < 0) ток практически не зави­сит от напряжения и равен тепловому току перехода (току насыще­ния). Этот ток обусловлен неоснов­ными носителями (дырками n-облас­ти и электронами р⁺-области). При значительном увеличении |U| обрат­ный ток резко возрастает. Это проис­ходит при U = , когда возникает лавинный пробой. Отметим, что в этой области, которая для лавинных диодов является рабочей, регулиро­вание тока осуществляется внешней цепью. Для стабилизации выбранно­го режима необходимо использовать источник питания с большим внутренним сопротивлением или вклю­чить последовательно с источником напряжения балластный рези­стор, сопротивление которого должно быть значительно больше дифференциального сопротивления диода на лавинном участке характеристики. При >>значение токаI будет ограничено со­противлением балластного резистора и равно (E -)/.