3.6. Параметры и модель р-n-перехода в динамическом режиме

3.6.1. Дифференциальное сопротивление

Оно определяется выражением R_диф = dU/dI и характеризует крутизну ВАХ (рис. 3.19,а) в рассматриваемой точке (R_диф обратно пропорциональна производной dI/dU). Для идеализированного пе­рехода по формуле (3.40) можно получить аналитическое выраже­ние

(3.51)

Для прямой ветви ВАХ, где I >>I₀,

(3.51 a)

При комнатной температуре _T = 0,026 В. Выразив I в миллиамперах, получим ши­роко используемую для оценок формулу

(3.52)

Зависимость R_диф и статического соп­ротивления R_ст = U/I от напряжения показана на рис 3.19,б. При прямом напряжении R_диф мало и убывает с ро­стом напряжения, а при обратном очень велико. Дифференциальное со­противление называют также сопро­тивлением переменному току. Пусть на ВАХ взята точка А (рабочая точка), соответствующая постоянному напря­жению U источника питания. Пусть по­следовательно с источником питания включен генератор переменного напряжения с малой амплиту­дой (U_m << _Т = 0,026 В). Сопротивление цепи для переменного тока равно U_m/I_m. Но значения малых амплитуд U_m и I_m можно заменить малыми приращениями U и I, т.е. U_m/I_m = U/I, а последнее совпадает с определением дифференциального сопротивления.

3.6.2. Барьерная емкость

Обедненный слой перехода подобен конденсатору, так как в нем «связаны» равные по величине, но противоположные по зна­ку заряды ионов акцепторов Q_a и доноров Q_д (|Q_a| = Q_д). Так как эти заряды определяют потенциальный барьер, то и емкость на­зывается барьерной.

Через обычный конденсатор, к которому приложено переменное напряжение, притекает ток смещения, не связанный с движением зарядов. Такой же ток смеще­ния появляется и при пере­менном напряжении на пере­ходе. Поясним это с помощью рис. 3.20 и понятия толщины р-n-перехода (см. § 3.3.2.).

Пусть произошло увели­чение обратного напряжения на небольшую величинуU. Толщина обедненного слоя возрастет: левая его граница сместится на небольшую ве­личину I_р, а правая – на I_n, так как возросшее поле в обедненном слое уносит дырки из слоя в р-область, а электроны из слоя I_р – в n-область, создавая в этих областях дырочный и электронный токи проводимости. Однако внутри обедненного слоя никакого дополни­тельного движения носителей заряда не возникает, цепь тока за­мыкается за счет тока смещения, связанного с изменением заряда Q_a на Q_а, а Q_д на Q_д, причем |Q_а| = Q_д.

По определению ток смещения I_см =₀ дЕ/дt = дQ/дt. Это соот­ношение можно записать в виде

(3.53)

где

(3.54)

называется дифференциальной барьерной емкостью р-п-перехода.

Если приращение напряжения мало, то изменения толщины слоя I_р и I_n малы. Следовательно, можно считать, что переход эк­вивалентен конденсатору, «обкладками» которого являются тонкие слои I_р и I_n, находящиеся на расстоянии, равном исходной толщи­не обедненного слоя I (I_р << I, I_n << I). Приращение заряда Q про­исходит на этих «обкладках», так как между ними нет изменения за­рядов. Поэтому можно написать общую формулу для барьерной ем­кости как емкости плоского конденсатора:

(3.55)

Подставив в (3.55) толщину перехода I из формулы (3.15) и про­изведя преобразования, получим зависимость С_б от напряжения и других параметров для резкого р-n-перехода:

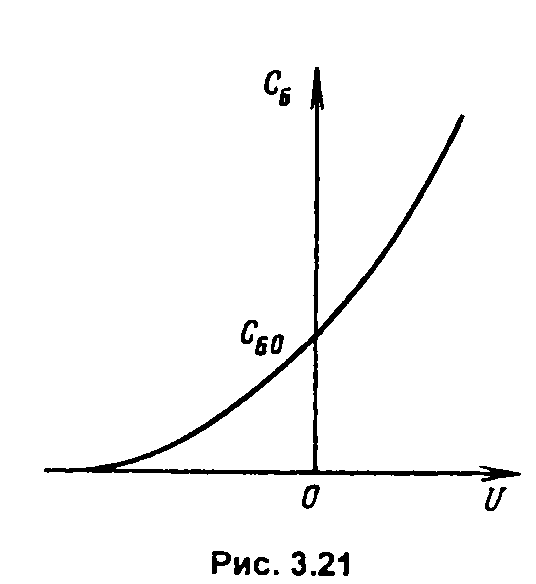(3.56)

ЗависимостьС_б от напряжения (вольт-фарадная характеристика) показана на рис. 3.21. Значение барьерной емкости пои U = 0

(3.57)

Используя (3.57), можно переписать (3.56) в более простом виде:

(3.58)

По формуле (3.58), требующей уточне­ния при ,. Такое увеличе­ние объясняется тем, что при этом обедненный слой (переход) становится бесконечно узким ().

Для плавного р-n-перехода в формулах для С_б вместо корня квадратного входит корень кубический. В общем случае вместо (3.58) пишут

где п = 1/2 – для резкого перехода, а п= 1/3 – для плавного перехода. Показатель п можно определить по экспериментальной вольт-фарадной характеристике.

Изменение зарядов в приграничных слоях обедненного слоя при переменном напряжении можно рассматривать как зарядку и раз­рядку плоского конденсатора.