2.2.2. Плотность тока в полупроводнике

В общем случае ток в полупроводнике обусловлен дрейфо­вым и диффузионным движением носителей заряда – электронов и дырок. Поэтому плотность тока представляется суммой четырех компонентов:

где индексы «др» и «дф» указывают на дрейф и диффузию.

Дрейфовым движением называют направленное движение носителей под действием напряженности электрического поля (градиента потенциала).

Плотность дрейфового тока в соответствии с общим опреде­лением

(2.48)

где и – дрейфовая скорость электронов и дырок, пропорци­ональная напряженности электрического поля Е:

(2.49)

Коэффициенты иназываютподвижностью электронов и дырок. Подставив (2.49) в (2.48), получим

(2.50)

Эти формулы часто записывают в виде

(2.51)

где, – удельные электрические проводимости, вы­званные электронами и дырками.

У германия = 3900 см/Вс,= 1900 см/Вс, а кремния= 1500 см/Вс,= 450 см/Вс. То, что подвижность электронов вы­ше подвижности дырок, имеет большое практическое значение; у германия они выше, чем у кремния.

Диффузионные компоненты плотности тока при одномерном рассмотрении определяются градиентами концентраций подвиж­ных носителей, т.е.

(2.52)

где и– коэффициенты диффузии электронов и дырок, завися­щие от материала полупроводника.

При диффузии носители перемещаются через выбранное сече­ние из области, где их концентрация больше, в область, где она меньше (рис. 2.7). Если принятьdn/dx > 0 и dp/dx > 0 (концентрация растет по оси х), то электроны и дырки перемещаются против оси х. Поэтому > 0 (совпадает с направлением оси х), a < 0 (про­тив оси, поэтому поставлен знак «минус» в (2.52)).

Существует пропорциональность между коэффициентами диф­фузии и подвижностью, называемая соотношением Эйнштейна:

(2.53)

где

(2.53а)

называется температурным или тепловым потенциалом. При T=З00 К =0,026 В.

2.2.3. Уравнение непрерывности

В общем случае концентрация носителей зависит от координаты и времени: n(x,t), p(x,t). Эти зависимости можно найти, решив урав­нение непрерывности, записываемое в виде:

для неосновных носителей в р-полупроводнике

(2.54)

для неосновных носителей в n-полупроводнике

(2.55)

В правой части каждого уравнения в частных производных пер­вый член учитывает убыль избыточных носителей ивследствие рекомбинации, как в выражении (2.44). Второй член учитывает накопление (или убыль) носителей в единице объе­ма из-за неодинаковости диффузионных потоков, втекающих в объ­ем и вытекающих из объема по направлению осих. Остальные чле­ны учитывают аналогичное влияние дрейфовых потоков.

В частном случае, когда в полупроводнике отсутствует электри­ческое поле (Е = 0) или его влиянием можно пренебречь, уравнения непрерывности упрощаются и принимают вид

(2.56)

(2.57)

Эти уравнения учитывают процесс диффузии и рекомбинации и называются уравнениями диффузии.

В полупроводниковых приборах часто рассматривается стацио­нарный режим, когда концентрации не изменяются во времени (dn/dt=0, dp/dt=0).

Рассмотрим p-полупроводник, в котором dn/dt=0. Тогда вместо (2.56) можно записать

(2.58)

где принято обозначение

(2.59)

Так как – избыточная концентрация электронов, то вместо (2.58) запишем

(2.60)

Решением этого дифференциально­го уравнения второго порядка является сумма экспонент:

(2.61)

а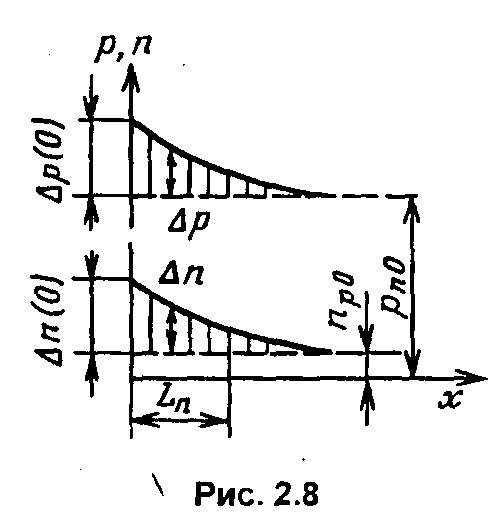коэффициентыиопределяются из граничных условий. Избыточную кон­центрацию прих=0 обозначим (0), а избыточную концентрацию при примем равной нулю (=0), считая, что в конце длинного образца полупро­водник остается в равновесном состоя­нии (n =). При таких граничных условиях получим=0, . Тогда распределение избыточной концентрации вдоль полупро­водника из (2.61) имеет вид (рис. 2.8)

(2.62)

Из выражения (2.62) следует, что при . Характерную длину , на которой избыточная концентрация электронов при диффузии уменьшается из-за рекомбинации в е =2,72 раза, называют диффузионной длиной электронов. При х > 3 уже можно считать, что, т.е. состояние счита­ется равновесным.

Аналогично (2.62) можно записать и закон изменения избыточ­ной концентрации дырок в n-полупроводнике:

(2.63)

где, как и в (2.59),

(2.64)

– диффузионная длина дырок в n-полупроводнике.