9

Сигналы и линейные системы

Тема 12: передача сигналов по кабелям

Все должно быть изложено так просто, как только возможно, но не проще.

Альберт Эйнштейн. Немецкий физик, ХХ в.

Осталось установить границу возможного и выкинуть излишние подробности. Для теоретиков не составит труда отнести эти подробности к известным по умолчанию. А практики хорошо знают принцип лишней детали - никогда не известно, для чего она нужна, пока не выбросишь.

Владислав Микшевич. Уральский геофизик, ХХ в.

Содержание: Введение. 12.1. Основное уравнение кабельной линии. 12.2. Волновое сопротивление кабельной линии.12.3. Режимы передачи сигналов кабельной линией. Режим бегущей волны. Режим стоячей волны. Режим несогласованной нагрузки. Задержка сигналов в кабеле.Литература.

Введение

Передача электрических сигналов по кабельным линиям связи обычно рассматривается в рамках общей теории однородных длинных видеолиний – симметричных и коаксиальных кабельных линий передачи аналоговых, дискретных и цифровых сигналов в спектре частот 0...10 МГц. Современное промышленное производство практически невозможно без стационарных и широко разветвленных внешних и внутренних линий связи.

Внутренние линии связи, управления, сбора и обработки данных в геологоразведочных и горнопромышленных отраслях производства в силу его специфики имеют свои особенности. Обычно они относятся к пассивным каналам связи и работают в условиях жестких климатических, механических и химических дестабилизирующих факторов на высоком уровне внешних электромагнитных помех. Как правило, эти каналы связи являются многожильными и для защиты от внешних факторов имеют общий стальной экран (оплетку), что существенно ограничивает частотные параметры передачи сигналов.

12.1. Основное уравнение кабельной линии [7,23]

Однородная кабельная линия, эквивалентная электрическая схема которой приведена на рис. 12.1.1, определяется первичными электрическими параметрами: погонными значениями активного сопротивления R, индуктивности L, емкости С и проводимости G на единицу длины линии (как правило, на 1 км). На вход линии подключается источник сигналов (генератор, передатчик) с выходным сопротивлением Z_o, на выход линии – приемник сигналов с входным сопротивлением Z_н (нагрузка линии).

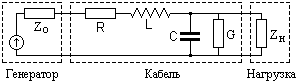
Рис. 12.1.1. Кабельная линия передачи сигнала.

По своей физической природе первичные электрические параметры кабеля аналогичны параметрам колебательных контуров, но в отличие от них они являются не сосредоточенными, а распределены по всей длине кабеля. Этим объясняется определенная зависимость первичных параметров кабеля от частоты сигнала и от конструкции кабеля.

Сигнал на входе линии задается в виде временной функции напряжения и тока. На выходе линии (на нагрузке) соответственно имееми. Падение напряжения и утечка тока на произвольном участке dx линии определяются уравнениями:

-d /dx = (R+jL),

-d /dx = (G+jC).

Решение данных уравнений для напряжения и тока в произвольной точке х линии дает следующие выражения /2/:

=ch x – sh x, (12.1.1)

=ch x – (/)sh x, (12.1.2)

= (R+jL)/ , (12.1.3)

где волновое сопротивление кабеля,  - коэффициент (постоянная) распространения линии (сигнала в кабеле):

 =  + j =, (12.1.4)

В выражениях (12.1.1)-(12.1.2) первые члены правой части представляют собой уравнения падающих волн напряжения и тока, распространяющихся по кабелю от генератора к нагрузке, а вторые члены – уравнения волн, отраженных от конца кабеля, энергия которых не поглотилась в нагрузке. Коэффициенты и относят к вторичным параметрам кабеля. Выражения действительны для любой точки кабеля, в том числе и на нагрузке кабеля при x = , где  – длина кабеля. Коэффициенты  и  являются собственными коэффициентами (собственными постоянными), соответственно, амплитудного затухания и фазового сдвига волны напряжения, проходящей через кабель. Их величины обычно задаются в значениях на 1 км кабеля и в этом случае называются километрическими (хотя последнее часто опускается и подразумевается по умолчанию). Численное значение километрического коэффициента  определяет коэффициент затухания волны напряжения, проходящей через кабель длиной 1 км. Соответственно, численным значением километрического коэффициента  задается величина сдвига фазы волны напряжения, проходящей через однокилометровый кабель.

 = , (12.1.5)

 = . (12.1.6)

Кабель, удовлетворяющий уравнениям 12.1.1-12.1.6, является идеальным кабелем передачи сигналов. Реальный кабель может существенно отличаться от идеального. Но основной характер зависимостей вторичных электрических параметров кабелей от первичных и качественную картину передачи сигналов по кабелю в различных условиях согласования с источником сигналов и нагрузкой целесообразно выяснить сначала на идеальном кабеле.