7.4. Пример графа предпочтений

Отношением нестрогого порядка (обозначение ) называется рефлексивное, антисимметричное и транзитивное отношение. Отношением строгого порядка (обозначение <) называется антирефлексивное, асимметричное и транзитивное отношение. Отношение нестрогого порядка можно рассматривать как объединение отношений < и ~.

Н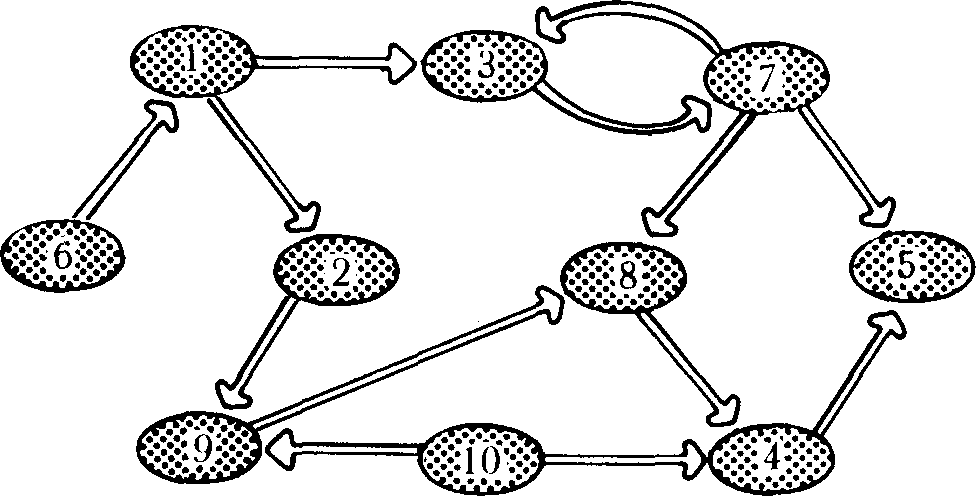 аконец, отношением доминирования называется отношение, обладающее антирефлексивностью и асимметричностью. Говорят, что "x доминирует у" (обозначается x>>y), когда x в каком-то смысле превосходит y. (Очевидно, строгий порядок - частный случай доминирования, при котором имеет место еще транзитивность.)

Хотя при подробном рассмотрении выбора потребуются и другие факты теории отношений, введенные понятия позволяют составить представление о возможностях данного языка.

В случае конечных множеств X очень удобно находить наилучшие альтернативы с помощью графа предпочтений, стрелки которого направлены в сторону менее предпочтимой альтернативы (рис. 7.4). Выделив вершины графа, из которых стрелки только исходят (альтернативы 6 и 10 на рис. 7.4), мы находим недоминируемые, т.е. наилучшие альтернативы. Можно показать, что если граф сильно транзитивен (т.е. транзитивен и по наличию, и по отсутствию стрелок) и антирефлексивен (отсутствуют петли), то описываемый выбор сводится к однокритериальному выбору. Другие типы графов описывают другие ситуации выбора.

Несмотря на то, что язык бинарных отношений введен для описания более общих и сложных ситуаций, нежели те, которые описываются критериальным языком, в чисто познавательных целях поучительно проследить, как уже известная нам ситуация выглядит в новом представлении.

Р ис.7.5. Описание паретовского множества как множества таких альтернатив, для которых верхнее сечение Р* (х) пусто

Например, многомерное критериальное пространство (с теми оговорками о соотношении размерностей критериев, которые были сделаны в предыдущем параграфе) может быть поставлено в соответствие евклидову пространству. Введение на этом пространстве бинарных отношений требует учета его свойств. В частности, начинают играть роль отношения инвариантные (относительно переноса), для которых верхнее сечение в любой точке может быть получено параллельным переносом верхнего сечения в любой другой точке. Примером инвариантного отношения является отношение Парето P:

Верхнее сечение отношения P есть первый квадрант с началом в точке x; теперь понятно, как находится паретовское множество альтернатив (на рис. 7.5 приведен случай конечного множества X, сравните этот рисунок с рис. 7.1,г): в паретовское множество включаются альтернативы, верхнее сечение которых пусто (на рис. 7.5 они отмечены кружками) .

В общем же случае выделение наиболее предпочтительных альтернатив возможно с помощью понятия оптимальности по отношению R, позволяющего придавать разный смысл понятию "наилучший" (задавая разные отношения R). Элемент xX называется мажорантой по отношению R на X, если для всех yX выполнено условие . Множество X₊(R) всех мажорант называется множеством R-оптимальных элементов.

ОБ ОЦИФРОВКЕ ПОРЯДКОВЫХ ШКАЛ

Важно обсудить ситуацию, возникшую при описании выбора на языке бинарных отношений в результате создания теории полезности [38] .П. Фишберн строго доказал теорему, смысл которой довольно ясен: если множество X конечно и между его элементами имеется отношение строгого порядка, то можно построить такую вещественную функцию u(x) на X, для которой

(x<y)[u(x)<u(y)]

(в левой части < означает отношение предпочтения, в правой – знак "меньше").

Функция u(x) называется функцией полезности. Ясно, что такая функция не единственна: произвольное монотонное преобразование сохраняет ее упорядочивающее свойство. Этот результат затем был обобщен на счетные и континуальные множества X, на нестрогий порядок и на многокритериальный случай (аддитивные функции полезности). Определение функции u(x) позволяет перейти от языка бинарных отношений к критериальному языку, взяв u(x) в качестве критериальной функции. Были развиты методы, позволяющие сузить класс функций полезности, например благодаря рассмотрению иерархических парных предпочтений (см. 6.2), повышая тем самым "точность определения u(x)".

Создается впечатление, что от качественных порядковых измерений можно перейти к количественным. На самом деле мы здесь вновь сталкиваемся с такой ситуацией, когда "оцифровка" порядковой шкалы не делает ее числовой шкалой. Для воспроизводства упорядочения фиксированного попарно упорядоченного множества X, конечно, можно воспользоваться числовой функцией u(x); однако стоит дополнить X альтернативами, которые не рассматривались при первом упорядочении, как функцию u(x) потребуется определять заново. Более того, если два разных эксперта дадут разные упорядочения множества X, то можно доопределить функции полезности для каждого из них, но сравнивать их численно иначе как в отношении порядка не имеет смысла (см. пример в 6.2), хотя обе они определены на одном множестве.

В тех случаях, когда количественная величина по каким-то причинам измеряется в порядковой шкале, оцифровка порядковых данных могла бы иметь смысл. Однако во многих приложениях теории полезности мы имеем дело с измерениями, которые в принципе не могут выйти из разряда порядковых.

Подведем итог В ряде практических случаев критериальная функция не существует, т.е. оценку данной альтернативе можно дать только в результате ее сравнения с другой альтернативой. Это потребовало более общего описания выбора. Первым таким обобщением и является язык бинарных отношений.