17. Помехоустойчивое кодирование. Помехоустойчивость кода. Корректирующие коды.

Помехоустойчивость кода.

Минимальное кодовое расстояние некоторого кода определяется как минимальное расстояние Хэмминга между любыми разрешенными кодовыми словами этого кода. У безызбыточного кода минимальное кодовое расстояние d_min=1. Чем больше минимальное кодовое расстояние, тем больше избыточность кода. Максимальное кодовое расстояние кода, очевидно, равно его размеру, т.е. числу двоичных разрядов в кодовом слове.

Непосредственные вычисления кодовых расстояний у рассмотренного выше кода, построенного методом контрольных сумм, дают следующие значения показателей: d_min=3 и d_max=7.

Очевидно, что -кратная ошибка приводит к тому, что искаженная кодовая комбинация отодвигается от исходной на расстояние. В то же время ошибка не может быть обнаружена, если она переводит одну разрешенную кодовую комбинацию в другую, тоже разрешенную. Следовательно, способность кода обнаруживать все ошибки некоторой кратности зависит от минимального расстояния между разрешенными кодовыми словами: чем больше минимальное кодовое расстояние, тем большей кратности требуется ошибка для перевода любой разрешенной кодовой комбинации в другую разрешенную. Таким образом, можно утверждать, что код с минимальным кодовым расстояниемd_min способен обнаруживать любые ошибки кратностью

У рассмотренного выше кода d_min=3, следовательно, он может обнаруживать любые однократные и двукратные ошибки.

Способность кода исправлять обнаруженные ошибки состоит в возможности однозначного отнесения запрещенной кодовой комбинации к единственной разрешенной. Для этого необходимо, чтобы минимальное кодовое расстояние превышало расстояние, порождаемое действием двух любых ошибок. Действительно, в этом случае запрещенные кодовые комбинации, получающиеся в результате ошибок из одного кодового слова, никогда не совпадут с запрещенными комбинациями, получающимися в результате ошибок из любого другого кодового слова, а тем более – с другими разрешенными кодовыми словами. Таким образом, необходимо, чтобы выполнялось условие откуда следует

У рассмотренного выше кода, построенного методом контрольных сумм, d_min=3, следовательно, он может исправлять только любые однократные ошибки.

Рассмотрим n-разрядный код, основанный на n-кратном повторении каждого передаваемого символа. У него d_min= n. Следовательно, максимальная кратность обнаруживаемых ошибок равна, что соответствует случаю искажения всех символов, кроме одного. Максимальная кратность исправляемых ошибок равна (n-1)/2, что соответствует искажению «почти» половины всех символов. Это соответствует фиксации ошибки при обнаружении хотя бы одного неодинакового символа и исправлению ошибки на основе определения, каких значений больше.

Рассмотрим n-разрядный код, основанный на введении одного разряда контроля четности. У него d_min= 2, и, следовательно, максимальеная кратность обнаруживаемых ошибок равна 1, а исправляемых – 0 (код не способен исправлять ошибки).

Граница Хэмминга. Рассмотрим задачу немного иначе. Возьмём n-разрядный код и зададимся вопросом о том, сколько контрольных разрядов должно быть в каждом кодовом слове, чтобы код мог исправлять все ошибки заданной максимальной кратности (разумеется,).

Возьмём какое-либо разрешенное кодовое слово и подсчитаем общее число кодовых комбинаций, порождаемых из него всевозможными ошибками кратностью не выше . Ситуация отсутствия ошибок дает одну (исходную комбинацию). Все однократные ошибки, искажающие 1 изn разрядов, очевидно, порождают n комбинаций. Все двукратные ошибки, искажающие 2 из n разрядов, очевидно, порождают комбинаций, где- число сочетаний изn по m. Аналогичным образом все m-кратные ошибки, искажающие m из n разрядов, порождают комбинаций. Учитывая, что формально, получаем следующую формулу для числа кодовых комбинаций, приходящихся на каждое разрешенное кодовое слово:

.Общее число кодовых комбинаций n-разрядного кода составляет , следовательно, чтобы комбинации, порождаемые из одного разрешенного кодового слова, не переходили в комбинации, порождаемые из другого, и могли быть исправлены, необходимо, чтобы число разрешенных кодовых слов Q удовлетворяло условию .

Это есть так называемая граница Хэмминга для числа разрешенных кодовых слов.

Граница Хэмминга позволяет определить минимальное число контрольных разрядов, необходимых для исправления ошибок с заданной максимальной кратностью. Пусть в n-разрядном коде k информационных разрядов, тогда число разрешенных кодовых слов составляет . Подставляя это значение в формулу для границы Хэмминга, получаем

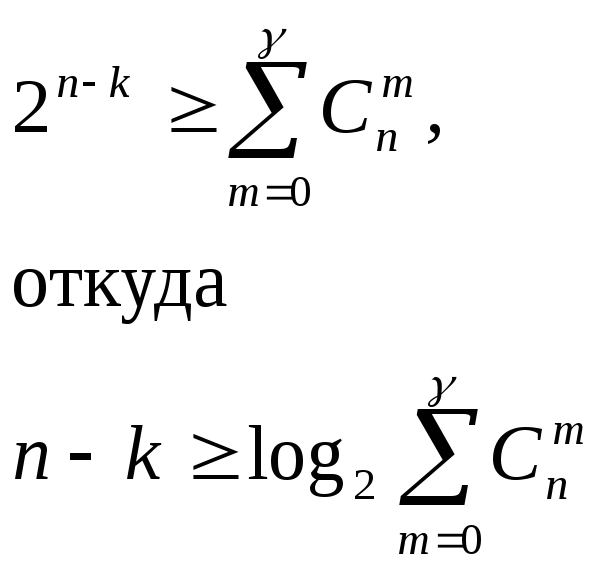
Величина n-k, как раз и есть минимальное число контрольных разрядов.

Коды, у которых число контрольных разрядов в точности совпадает с границей Хэмминга, называются совершенными. Совершенные коды обладают минимальной избыточностью при заданном уровне способности исправлять ошибки. В построенном выше примере 7-разрядного кода, исправляющего все однократные ошибки, использовалось 3 контрольных разряда. Подставляя параметры кода в полученную формулу, убеждаемся, что 3 – это минимальное количество контрольных разрядов, необходимое для решения задач, следовательно, код совершенный. Для более сложных случаев (большей кратности ошибок) не всегда удается построить совершенный код.

Классификация корректирующих кодов.

Математическая теория корректирующих кодов бурно развилась в 50-60-х годах XX века в обширную и практически важную самостоятельную науку, базирующуюся на казавшихся самыми абстрактными и далекими от практики разделах современной математики.

У большинства известных в настоящее время корректирующих кодов помехоустойчивость обеспечивается за счет их алгебраических свойств, в связи с чем их называют алгебраическими кодами.

Алгебраические коды подразделяются на два больших класса: блоковые и непрерывные (реккурентные).

В случае блоковых кодов кодирование заключается в сопоставлении каждому символу сообщения блока из n символов. Различают разделимые и неразделимые блоковые коды. В разделимых кодах четко разграничены информационные и контрольные (проверочные) символы. В неразделимых кодах все символы выполняют функции как информационных, так и контрольных.

Непрерывными (рекуррентными ) называются такие коды, в которых введение избыточных символов в кодируемую последовательность осуществляется без разделения её на блоки. Непрерывные коды также могут быть разделимыми и неразделимыми.

Большой класс разделимых кодов составляют систематические коды, у которых значения проверочных символов определяются в результате линейных операций над определенными информационным символами. Для случая двоичных кодов каждый проверочный символ выбирается таким, чтобы его сумма по модулю 2 с определенными информационными символами стала равной нулю, т.е. обеспечивалась четность некоторой контрольной суммы. Проверочные символы могут располагаться на любом месте кодовой комбинации. Их число и соответствующие проверочные равенства (контрольные суммы) определяются тем, какие и сколько ошибок должен обнаруживать или исправлять код.