20

СТРОЕНИЕ АТОМА. ПЕРИОДИЧЕСКИЙ ЗАКОН

И ПЕРИОДИЧЕСКАЯ СИСТЕМА Д.И. МЕНДЕЛЕЕВА. ХИМИЧЕСКАЯ СВЯЗЬ

Примеры решения задач

Задача 1. Желтый свет, испускаемый натриевой лампой, имеет

длину волны 589 нм. Какова частота этого излучения?

Дано: λ= 589 нм

с =3∙10⁸ м/с

ν=?

Решение. Из уравнения с= h∙ν находим ν = c/h. Подставляем в это уравнение значение с и h, преобразуя нм в м, получаем

Задача 2. Вычислите мельчайшую порцию энергии (т.е. квант энергии)

желтого света с длиной волны 589 нм, кото­рая может быть

поглощена телом.

Дано: λ =589нм

H=6,63∙10⁸ м/с

c=3∙10⁸ м/с

E?

Решение. Величина кванта энергии согласно уравнению Планка равна E=h∙ν. В задаче I найдено:

Зная ν, находим: ∆Е=hν =(6,63∙10^-34 Дж∙(5,09∙10¹⁴ с^-1)=3,37∙10^-19 Дж. Согласно теории Планка атом или молекула, испускающая или поглощающая излучение с длиной волны 589 нм, могут терять или приобретать энергию излучения только порциями, кратными вели­чине 3,37∙10^-19 Дж. Они не могут, например, получить от тако­го излучения энергию 5,00∙10^-19 Дж, поскольку это количество не является целочисленным кратным величине 3,37∙10^-19Дж.

Задача 3. Вычислить в электронвольтах энергию возбуждения электрона в атоме магния, если пары его поглощают фотоны с длиной волны 6600∙10^-19 м.

Дано: h=6,63∙10^-34Дж с

c=3,00∙10⁸ м/с

λ=6,600∙10^-10м,

∆Е=?

Решение. Энергия возбуждения электрона равна энергии поглощаемого фотона, которую можно рассчитать по уравнению Планка Е = h∙ν и по соотношению ν = c/λ. Согласно этим двум уравнениям записываем выражение для энергии возбуждения фотона Е = h∙ν = h∙ c/λ:

Е = 6,63∙10^-34 =3,410^-19 Дж .

Сделаем пересчет Дж в эВ, исходя из того, что 1 Дж = 0,624∙10^-19 эВ; отсюда Е возбуждения будет равна Е = 3,4∙10^-19 0,624∙10^-19 = 2,12∙10^-39 эВ.

Задача 4. Вычислить массу фотона, соответствующую линии серии Бальмера, если отвечающая ей длина волны λ равна 6563∙10^-10м.

Дано: h = 6,63∙10^-34 Дж с

C = 3∙10⁸м/с

λ = 6563 10^-10 м

m_фотона – ?

Решение. Из уравнения Луи де Бройля находим, что m = h/λc. Подставляя числовые значения, получим, что

Задача 5. Вычислите длину волны де Бройля, которая соответствует электрону с массой 9,1∙10^-31 кг, движущемуся со скоростью 6∙10⁶ м/с.

Дано: m_l = 9,1∙10^-31кг

V_ф = 6∙10⁶ м/с

h = 6,63∙10^-34 Дж

λ – ?

Решение. Подставляя имеющиеся значения в уравнение де Бройля , получим

Задача 6. Вычислить частоту линии в спектре атомарного водорода, которая соответствует переходу электрона из состояния с n=4 в состояние n = 2.

Дано: n_i - квантовое число исходной орбиты=4

n_f - квантовое число конечной орбиты=2

ν = ?

Решение. Подставим в уравнение значения n_i =4 и n_f=2, так как это и есть квантовые числа, исходной и конечной орбит соответственно:

Отсюда

Задача 7. Вычислите энергию, необходимую для ионизации электрона из основного состояния атома водорода.

Дано: Rн = 2,18 ∙10^-18 Дж

n_f = ∞

n_i = 1

∆Е=?

Решение. Энергию ионизации можно записать как разность между энергиями конечного состояния n_f и исходного состояния n_i: .

Следовательно, ∆E = Rн =2,18∙10^-18Дж, полученную величину удобнее выражать в расчете на моль атомов. Для этого ее нужно умножить на число Авогадро:

∆Е = (2,18 10^-18) Дж/атом (6,02 10²³ атомов/моль)/1000= =1,31∙10³ кДж/моль.

Задача 8. Определите энергию (эВ), которой обладает электрон,

находясь на втором энергетическом уровне в атоме водорода.

Дано: n = 2

E = ?

Решение. Для решения задачи применим уравнение (1): En= - Rн z²/n² · Е = -13,6 z²/n², где z- заряд ядра атома, n номер энергетического уровня. Энергия электрона на втором энергетическом уровне равна E=13,6∙1/2² эВ = 3,40 эВ.

Задача 9. Длины волн линий Н_α и Н_β серии Бальмера ооответственно равны 6563∙10^-10 и 4102∙10^-10 м. Во сколько раз масса одного фотона (какого?) больше массы другого?

Дано: h=6,626∙10^-34 Дж с

с=3∙10⁸ м/с

Н_α=6563∙10^-10м

H_β=4102 ∙10^-10м

mH_β / mН_α=?

Решение. Массу протона вычисляют по уравнению де Бройля, принимая скорость фотона равной скорости света с = 3∙10⁸ м/с:

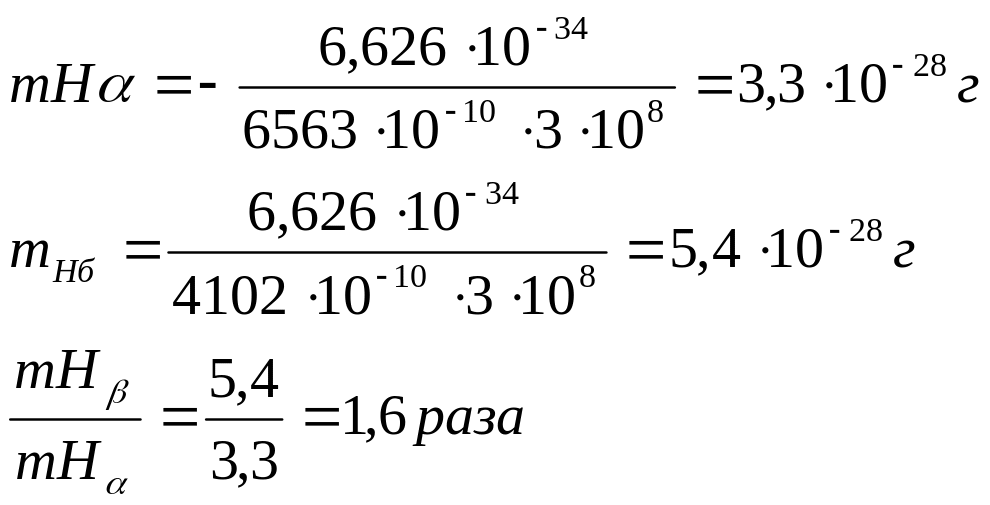
Ответ: mH_β в 1,6 раза больше mH_α.

Задача 10. Определите частоту излучения и длину волны 2-й линии (H_β) серии Бальмера спектра атомарного водорода.

Дано: h=6,63∙10^-34Дж с

Rн=3,29∙10^-15

или 2,18∙10^-18 Дж/ат; υ - ? λ - ?

Решение. Линия H_β в серии Бальмера атомарного спектра водорода образуется при переходе электрона из состояния n=4 в состояние n =2.

Подставим в уравнение (3) n=4 и n=2, так как это и есть квантовые числа исходной и конечной орбит соответственно:

Отрицательный знак полученной величины указывает, что атом испускает свет. Из уравнения с = hν вычислим λ (длину волны излучения).

или 4860А⁰

КВАНТОВЫЕ ЧИСЛА. ПРИНЦИП ПАУЛИ. ПРИНЦИП НАИМЕНЬШЕЙ ЭНЕРГИИ. ЭЛЕКТРОННЫЕ ФОРМУЛЫ.

ПРАВИЛО ХУНДА

Примеры решения задач

Задача 1. Определите, сколько подуровней и орбиталей может быть в 5-м энергетическом уровне.

Решение. Число подуровней определяется орбитальным квантовым числом l , которое принимает значение от 0 до (n-1). Если n=5, то l=0,1,2,3,4. Число подуровней на 5 уровне равно 5.

Известно, что ориентацию орбиталей в пространстве и возможное число орбиталей характеризует магнитное квантовое число m_l, которое принимает значение от –l, 0, +l.

В данной задаче l = 0, 1, 2, 3, 4. Если l = 0(s), m_l = 0, это значит, что в случае орбитали шаровой симметрии возможна только одна ее ориентация, т.е. число орбиталей равно 1; если l = 1(p), то m_l принимает значения –l,0,+1, т.е. число орбиталей на р-подуровне равно 3; l=2, то m_l принимает значения от -2,-1,0,1,2, т.е. число орбиталей нa d-подуровне равно 5; m_l=3(f), m_l принимает значения от -3,-2,-1,0,1,2,3, т.е. число орбиталей на f подуров­не равно 7; m_l =4(g), m_l принимает значения -4,-3,-2,-1,0,1,2,3,4, т.е. возможное число орбиталей на g-подуровне равно 9. Таким образом, максимально возможное число орбиталей на 5 уровне равно 1+3+5+7+9=25.

Задача 2. Написать электронные формулы атомов йода и вольфрама.

Решение. Для распределения электронов в многоэлектронном атоме воспользуемся принципом Паули и правилами Клечковского. Энергия электрона в атоме определяется значением (n+l) –суммой главного и орбитального квантовых чисел, последовательность заполнения электронами отдельных подуровней происходит в порядке последовательного увеличения суммы (n+l) (1-е правило Клечковского), а при одинаковых значениях суммы - в порядке последовательного возрастания главного квантового числа - (2-е правило Клечковского). Атом иода находится в 5-м периоде, порядковый номер 53. Для распре­деления электронов предварительно можно для каждого уровня написать значения подуровней и (n+l) (см. таблицу). Заполнение ведем согласно 1-му правилу Клечковского, а с четвертого уровня прибегаем ко 2-му правилу, т.е. если у 2-х квантовых слоев, как у нас, n=3 и n =4, сумма (n+l) равна 4 - (3+1) и (4+0), то после суммы (3+1), заполняется сумма(4+0). Да­лее заполняем сумму 5, которая повторяется в 3-х квантовых слоях 3,4,5 (3+2, 4+1, 5+0). В этом случае вначале заполняем сумму от меньшего n к большему l, т.е. 3d, 4р, 5s по принципу на­именьшей энергии, следующая возрастающая сумма (n+l)=6, она наблюдается также в 3-х квантовых слоях (4+2, 5+1, 6+0). Таким образом распределим 53 электрона атома йода по 2-м кванто­вым числам 1s², 2s², 2p⁶, 3s², Зр⁶, 4s², 3d¹⁰, 4p⁶,5s²,4d¹⁰, 5p⁵.

Номер периода	n=1	n=2	n=3	n=4	n=5	n=6
Значе-ние l	l=0(s)	l=0(s), 1(p)	l=0(s), 1(p),2(d)	l=0(s),1(p),2(d),3f	l=0(s),1(p),2(d),3f,4d	l=0(s), 1(p),2(d), 3f,4d,5(…
Сумма	(n+l)	(n+l)	(n+l)	(n+l)	(n+l)	(n+l)
	1+0(s)=1	2+0(s)=2	3+0(s)=3	4+0(s)=4	5+0(s)=5	6+0(s)=6
		2+1(p)=3	3+1(p)=4	4+1(p)=5	5+1(p)=6	6+1(p)=7
			3+2(d)=5	4+2(d)=6	5+2(d)=7	6+2(d)=8
				4+3(f)=7	5+3(f)=8	6+3(f)=9
					5+4(q)=9

Атом вольфрама находится в 6-м периоде, порядковый номер 74; распределим электроны аналогично атому йода:

1s²,2s²,2p⁶,3s²,3р⁶,4s²,3d¹⁰,4р⁶,5s²,4d^I0,5p⁶,6s² ,4f¹⁴,5d⁴.

Задача 3. Определить последовательность заполнения электронами подуровней в атомах элементов, если их суммы (n+l) соответственно равны 5 и 6.

Решение. n+l =5 n+l=6

n=3, n=4,

l=2, l=1, l=0 l=3, l=2, l=1, l=0

n=4, n=5,

l=3, l=2, l=1 l=0 l=4, l=3, l=2, l=1 l=0

n=5 n =6

l=4, l=3, l=2, l=1 l=0 l=5, l=4, l=3, l=2, l=1 l=0

3+2 4+1=5 5+0=5 4+2=6 5+1=6 6+0=6

Таким oбpaзoм, последовательность заполнения электронами подуровней в атомах элементов, если сумма n+l = 5, от 3d→4p 5s, а в случае суммы n+l =6 - от 4d 5p 6s.

Задача 4. Напишите электронные конфигурации следующих ионов: AI³⁺, Cr³⁺, Fe²⁺, Fe³⁺, Cl.

Р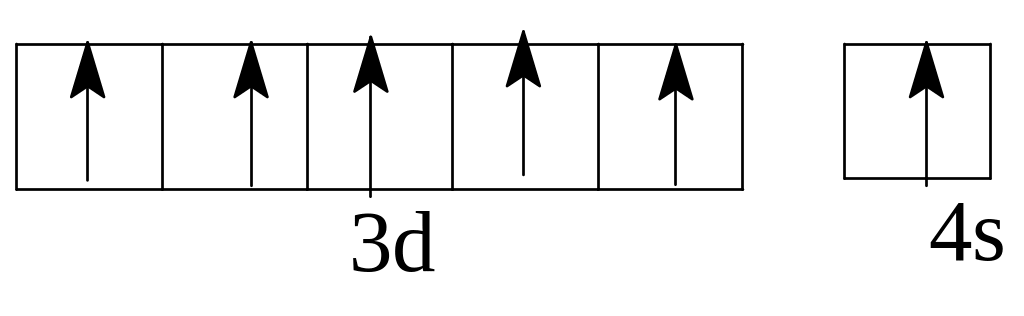 ешение. Положительно заряженные ионы образуются в том случае, когда от нейтрального атома под действием энергии извне отрываются электроны. Отрицательно заряженные ионы образуются при присоединении к нейтральному атому электронов. Нейтральный атом алюминия имеет следующую электронную конфигурацию: ₁₃Al 1s²2s²2р⁶3s²3р¹, последний застраивающийся слой 3s²3р¹. В том случае, когда атом алюминия (Al) превращается в ион Al³⁺, от нейтрального атома отрывается 3 электрона, имеющие наибольшую энергию, т.е. с 3s и 3р-подуровней, вследствие чего ион имеет следующую электронную конфигурацию: 1s²2s²2р⁶3s⁰3р⁰. Нейтральный атом хрома имеет электронную конфигурацию ₂₄Cr 1s²2s²2p⁶3s²3р⁶4s¹3d⁵, последний застраивающийся 3d – подуровень:

При отрыве от нейтрального атома 3-х электронов в первую очередь будут отрываться: один электрон с подуровня 4s и два электрона с подуровня 3d. При этом атом хрома превращается в ион Cr³⁺ и его электронная конфигурация будет такова 1s² 2s² 2p⁶ 3s² 3р⁶ 4s°3d³.

Нейтральный атом железа имеет следующую электронную конфигурацию ₂₆Fе 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d⁶. При отрыве от атома 2 электронов атом превращается в ион Fе²⁺: 1s² 2s² 2р⁶ 3s² 3р⁶ 4s° 3d⁶. При отрыве от атома 3 электронов, атом превращается в ион Fe³⁺: 1s² 2s² 2p⁶ 3s² 3p⁶4s°3d⁵. Нейтральный атом хлора имеет следующую электронную конфигурацию ₁₇Cl 1s² 2s² 2p⁶ 3s² 3p⁵ ; приобретая один электрон, атом превращается в отрицательно заряженный ион Сl^-: 1s²2s²2p⁶3s²3p⁶

Задача 5. Какие ошибки допущены в схемах распределения электронов

внешних слоев в невозбужденном состоянии атомов:

а) Бор (В)

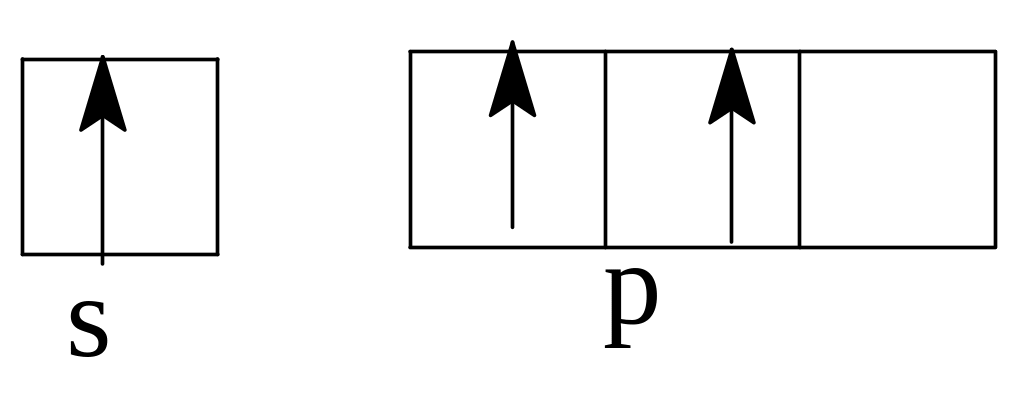
б)Азот (Ш)

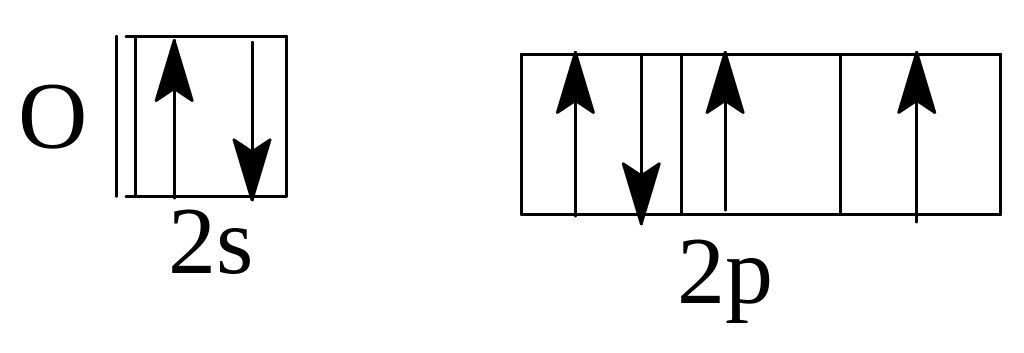
в) Кислород (0)

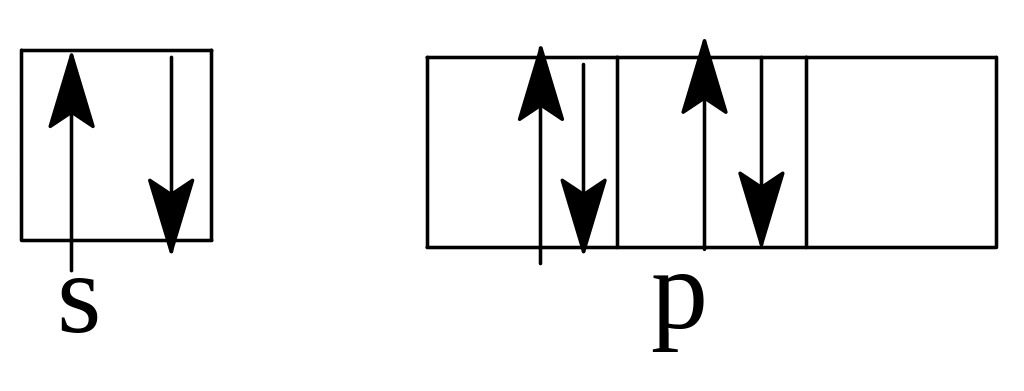
Решение. а) В невозбужденном атоме бора по принципу наименьшей энергии должен вначале заполниться полностью s-подуровень второго

у ровня, а затем электронами заполняется р-подуровень. Правильное распределение 2s²2р¹. В случае (б) и (в) не выполнено правило Хунда. Электроны в пределах подуровня должны распределяться так, чтобы суммарное спиновое квантовое число было максимальным. Правильное распределение:

Задача 6. Какие вакантные орбитали, способные влиять на химические свойства элементов, имеются у атомов титана, криптона, урана?

Решение. На химические свойства элементов оказывают влияние лишь вакантные орбитали с относительно низкой энергией. Обычно это d-орбитали предпоследнего слоя. Также можно отметить, что на химические свойства элементов могут оказывать влияние вакантные (n–1) f-орбитали. На хи­мические свойства титана в основном оказывают влияние наличие у его атомов 3d-и 4р-вакантных орбиталей, у атомов криптона 4d-, а у атомов урана 5f-,6d-,7p-орбитали.

Задача 7. Одинаковы ли по энергии и ориентации орбитали двух электронов со следующими наборами квантовых чисел:

1) n₁=3; l₁=0; m_(l)=0 m_(s)= ;

2) n₂=3; l₂=1; m_(l)=1 m_(s)=

Решение. Энергия электрона в атоме определяется суммой энергий главного и орбитального квантовых чисел (n+l). У первого электрона (n+l) равно 3+0=3, а у второго(n+l) (3+1 )=4. Следовательно, эти два электрона имеют различную энергию. Ориентация орбиталей электронов на данном подуровне определяется магнитным квантовым числом, в нашем примере у первого электрона m_(l1)=0, а у второго m_(l)=1. Следовательно, ориентация орбиталей у них различная.

Задача 8. Не обращаясь к табличным данным, определите количество орбиталей, для которых n = 4, укажите значения чисел n и m_l для каждой из этих орбиталей.

Решение. Для n = 4 возможные значения числа l таковы: 0,1,2,3. Это соответствует 4s-, 4р-, 4d-, 4f- подуровням. В них существуют одна 4s-орбиталь (n=4, l=0, m_l=0), три 4р-орбитали (n=4, l=1, m_l=1,0,+1), пять 4d- орбиталей (n=4, l=2, m_l=-2,-1,0,1,2) и семь 4f- орбиталей (n=4, l=3, m_l=-3,-2,-1,0,1,2,3).

Задача 9. Написать электронно-графические формулы атомов скандия, брома, молибдена в нормальном и возбужденном состоянии атома.

Решение. Электронные формулы заданных атомов в нормальном

(невозбужденном) состоянии :₂₁Sc 1s²2s²2p63s²3p⁶4s²3d¹

₃₅Br 1s²2s²2p⁶3s²3p⁶4s²3d ^I04 p⁵

₄₂Mo 1s²2s²2p⁶3s²3p⁶4s²3d^I04p ⁶5s¹4d⁵

Такие электронные формулы могут быть представлены графически:

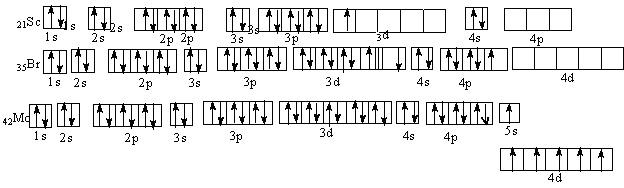
Однако наличие вакантных орбиталей у Sc в 4 уровне в подуровне 4р делает возможным возбуждение этих электронов до 4р у Sc и 4d у Вr с затратой сравнительно небольшой энергии. Электронные формулы возбужденных атомов скандия и брома таковы: Sc* 1 ²2 ²2p⁶3s²3p⁶4s^I3d¹4p^I

максимальное возбуждение Br***ls²2s²2p⁶3s²3p⁶4s^I3d¹⁰4p³4d³

3. ПЕРИОДИЧЕСКАЯ СИСТЕМА, ПЕРИОДИЧЕСКИЙ ЗАКОН Д.И.МЕНДЕЛЕЕВА, ПЕРИОДИЧНОСТЬ ИЗМЕНЕНИЯ СВОЙСТВ ЭЛЕМЕНТОВ