Как построить прямую, параллельную данной?

Пример

Прямая задана уравнением  . Составить уравнение параллельной прямой, которая проходит через точку  .

Решение: Обозначим неизвестную прямую буквой  .

Прямая   проходит через точку  . А если прямые параллельны, то очевидно, что направляющий вектор прямой c подойдёт и для построения прямой d.

Направляющий вектор берем из уравнения  :

Уравнение прямой   составим по точке   и направляющему вектору  :

Ответ: 

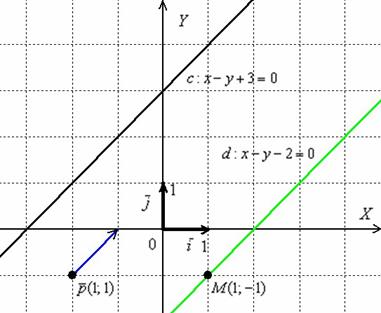
Иллюстрация примера:

Как найти точку пересечения двух прямых?

Если прямые   пересекаются в точке  , то её координаты являются решением СЛАУ:

Как найти точку пересечения прямых? Решить систему.

Геометрический смысл системы двух линейных уравнений с двумя неизвестными – это две пересекающиеся (чаще всего) прямые на плоскости.

Пример

Найти точку пересечения прямых  

Решение: Существуют два способа решения – графический и аналитический.

Графический способ состоит в том, чтобы просто начертить данные прямые и узнать точку пересечения непосредственно из чертежа: 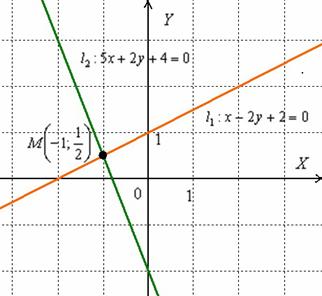Получилась точка  . Для проверки следует подставить её координаты в каждое уравнение прямой, они должны подойти и там, и там. Иными словами, координаты точки   являются решением системы  .

 Точку пересечения   целесообразнее искать аналитическим методом. Решим систему:

Ответ:

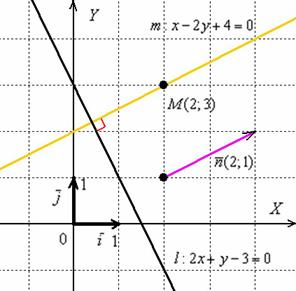
Как построить прямую, перпендикулярную данной?

Пример

Прямая задана уравнением  . Составить уравнение перпендикулярной прямой  , проходящей через точку  .

Решение: По условию известно, что  . Надо найти направляющий вектор прямой 

Из уравнения   находим вектор нормали:  , который будет направляющим вектором прямой  .

Уравнение прямой   составим по точке   и направляющему вектору  :

Ответ: 

Расстояние от точки до прямой

Расстояние от точки до прямой – это длина перпендикулярного отрезка.

Расстояние в геометрии традиционно обозначают греческой буквой «ро», например:   – расстояние от точки «эм» до прямой «дэ».

Расстояние от точки   до прямой   выражается формулой 

Пример

Найти расстояние от точки   до прямой 

Решение:

Ответ: 

Как найти угол между двумя прямыми?

Существуют две формулы.

Первый способ.

Рассмотрим две прямые, заданные уравнениями в общем виде:

Если прямые не перпендикулярны, то  угол   между ними можно вычислить с помощью формулы:

Рассмотрим знаменатель – это скалярное произведение направляющих векторов прямых:

Если  , то знаменатель формулы обращается в ноль, а векторы будут ортогональны и прямые перпендикулярны. Именно поэтому сделана оговорка о неперпендикулярности прямых в формулировке.

Второй способ.

Если прямые заданы уравнениями с угловым коэффициентом   и не перпендикулярны, то  угол   между ними можно найти с помощью формулы:  

Условие перпендикулярности прямых выражается равенством  , откуда следует полезная взаимосвязь угловых коэффициентов перпендикулярных прямых:  , которая используется в некоторых задачах.

Пример

Найти угол между прямыми  

Решение первым способом

Решение удобно оформить в два этапа:

1) Вычислим скалярное произведение направляющих векторов прямых: , значит, прямые не перпендикулярны.

2) Угол между прямыми найдём по формуле:

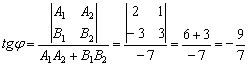
С помощью обратной функции легко найти и сам угол. При этом используем нечётность арктангенса:

Ответ: 

Решение вторым способом

Алгоритм решения похож на предыдущий пункт. Но сначала перепишем прямые в нужном виде:

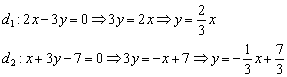
Таким образом, угловые коэффициенты: 

1) Проверим, будут ли прямые перпендикулярны: , значит, прямые не перпендикулярны.

2)  Используем формулу:

Ответ: 

13