Отношения и формальные сис-мы

Понятие форм-й сис-мы основано на понятии подстановки(редукции) на заданном мн-ве М объектов (символов, послед-тей сим-в, терминов).

//пр-р. это отн-ние рефлексивно, транзитивно и антисимметрично

= это отн-е эквивалентности, рефлексивно, транзитивно, симметрично.

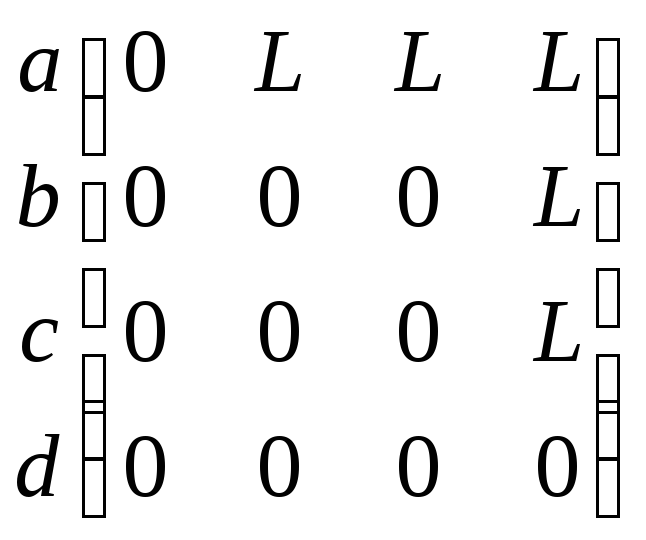
Буд.рассм-ть т/о однородные бинарные отн-я Rна мн-ве М, это мн-во пар (х,у) элементов хМ, уМ, кот-е нах-ся м/у собой в отн-нииRи явл-ся подмн-вом мн-ва ММ. Вместо бинарного отн-ияRна М м/о говорить об ориентированном графе (М,R), причем элементы М – это вершины графа, а пары изRэто дуги графа. Любым 2м вершинам х и у из М соответствует не более1й стрелки (х,у), кот-я их связывает. Кроме того любой вершине х из М и дуге рRсоотв-ет не более 1й вершины у, ведущей из вер-ны х, дуга в этом сл-е р=(х,у). Для конечных мн-в М отн-еRм.б.задано не т/о графически, но и в виде матриц, такие мат-цы наз-ся м-ми инцеденций.

a b c d a b c d a b c d

Замыкание

Рефлексивнымзамыкакнием (R^r) отн-нияRнад мн-вом М н-ся пересечение всех рефлексивных отн-ний над М, содержащихR.

//пр-р R= {(0,1),(1,1),(1,2)},M={0,1,2}, тогда рефл-м замыканием явл-ся мн-во

R^r={(0,0),(0,1),(1,1),(1,2),(2,2),(0,2)}

Транзитивным зам-ем (R⁺), бинарного отнош-ияRнад мн-м М н-ся перечение всех транзитивный отн-й над М, содер-хR.

R⁺= {(0,1),(0,2),(1,1),(1,2)}для нашего сл-я

Симметричноезамыкание (R^s),R^s=RR^T, гдеR^T- обращение бинарного отношенияR.

// для графического отображения – это просто перемена направления стрелок. Для нашего случая:

R^s= { (0,1), (1,0),(1,1),(1,2),(2,1)}

Транзитивно-рефлексивноезам-е (R^*) бинарного отн-нияRнад М – это пересечение всех транзитивных и рефлексивных отн-й над М, кот-е содержатR

Симметрично-транзитивно-рефлексивноезам-е (R^□) это пересечение всех сим-х, транзитивных и рефлективных отн-й над М, кот-е содержатR.

Под конечным путем длины i(i≠0) от вершины х к вершине у в графе (М,→) понимают последовательность стрелок х=х₀→х₁, х₁→х₂,…,х_i-1→x_i=y, здесь вершина х₀– начало пути, вершина х – конец пути х_iесть вершина у. Видно, что (х,у)Rⁱозначает то, что в графе (М,R) сущ-т путь длиныiот х к у. если последовательность стрелок бесконечна, то путь наз-т бесконечным. Отн-ние, а также ориентированный граф (М,→) наз-т НЕТЕРОВЫМ, если ни для какого х из М не сущ-т бесконечных путей исходящих из х. В нетеровом графе не м.б.циклов, т.е.путей длиной больше 1цы из некоторой вершины в нее же. Всякий путь в нетеровом графе явл-ся цепью, т.к.мн-во { х₀,х₁,…, x_i} упорядочено отношением → и х_μ≠х_η, μ≠η. Ориентированный граф тривиальным образом явл-ся нетеровым, если все пути в нем имеют ограниченную длину.

Редукция

Если сущ-т конечный путь из вер-ны х в вер-у у, что принято обозначать х→^*у, то говорят что х редуцируется к у. Элемент х из М наз-ся редуцируемым отн-но отношения (М,→), если сущ-т элемент у, т.ч.выполняется соотношение х→^*у. Путь длиныi(i≠0) из х в у в графе (М,→) наз-ся тупиковым, если элемент у нередуцируемый. В нетеровом графе для каж-го х из М сущ-т покарайней мере 1н неруд-й элемент у, тогда алгоритм редукции на нетеровых отношениях м.б.описан сл.образом.

«Начиная с некоторого элемента х совершайте переходы по стрелкам до тех пор, пока это возможно и остановитесь, когда встретится нередуцир-й элем-т». Перечисление промежуточных узлов редукции в порядке их появления представляет собой путь редукции.

Строки

Строка – это конечная последовательность символов а₁, а₂,…,а_n, каж-й из кот-х принадлежит некоторому конечному алф-ту Σ, при этом символы в стороке могут повторяться.

Если строка содержит mсимволов, то говорят что она имеет длинуm. Пустой строкой наз-т строку длины ноль, т.е.без единого символа и ее наз-т ε-строкой.(не путать с пробелом). |x|=m-длина строки.

Пусть Σ-некот-й алф-т, обозначим Σ^*мн-во опред-х над этим алф-м строк. Для Σ={0,1}; Σ^*= {ε,0,1,01,11,10,101,…} видно, что н-во Σ^*- предс-т собой бесконечное счетное мн-во элем-в, ε-строка всегдаΣ^*

Пусть сущ-т строка хΣ^*и |x|=m

Пусть сущ-т строка yΣ^*и |y|=n, тогда объединение строк ху им.длину |xy|=m+n– конкатенация.

Если х= а₁, а₂,…,а_m; у=b₁,b₂,…,b_nто |xy|= а₁а₂…а_mb₁b₂...b_n

Операция объединения строк – это ассциот-я операция, но не коммутативная. Для пустой строки справедливо εх=хε для люб.строки х.

Если некоторая срока zм.б.представлена как объединение строк х и у:z=ху, то строку х наз-т префиксом строкиz, а строку у-суффиксом.

//z=00111

префиксы: ε,0,00,001,0011,00111

суффиксы: ε,1,11,111,0111,00111

если строка zт.ч.ее м/о представить как объединение 3х строкz=xwy, то строкаwн-ся подстрокой строкиz.

Формальным языком Lнад алф-ом Σ н-ся произвольное подмн-во мн-ва Σ^*.