Федеральное агентство по образованию

Государственное общеобразовательное учреждение

высшего профессионального образования

Пермский государственный технический университет

Кафедра Автоматики и телемеханики

ОПТИМИЗАЦИЯ СТРУКТУРЫ СЕТЕЙ СВЯЗИ

Расчётно-графическая работа

Вариант M = 15 и N = 9

Выполнил студент __________________________________________

подпись, дата

Группа

Проверил преподаватель_____________________________________

подпись, дата

Пермь 2011

Оглавление

1. Подготовка исходных данных 3

2. Расчёт сети с МПВ 4

3. Расчёт сети с МПС 6

4. Расчёт сети с МКЗ 12

17

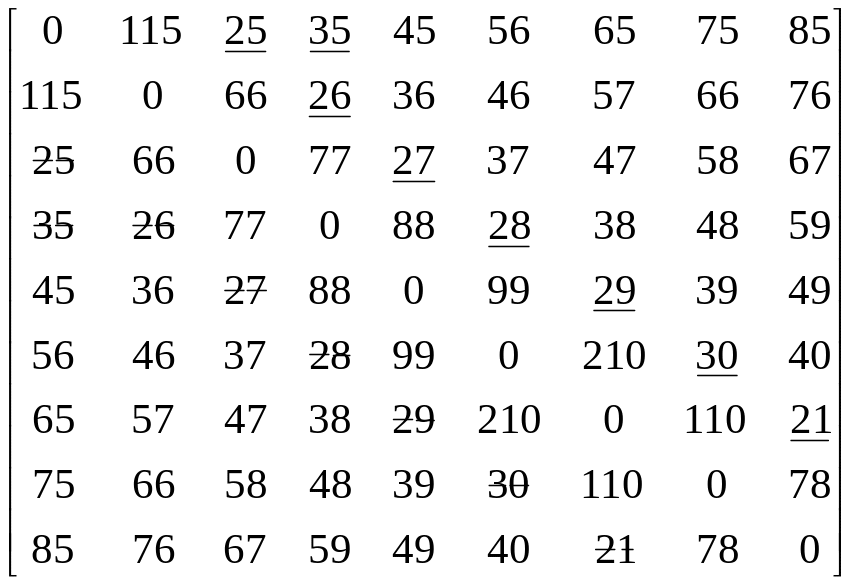
1. Подготовка исходных данных

Номер по журналу M = 15, число станций сети N = 9.

Из таблицы приложения 1 выписываем расстояния между пунктами сети :

Из таблицы приложения 2 составляем :

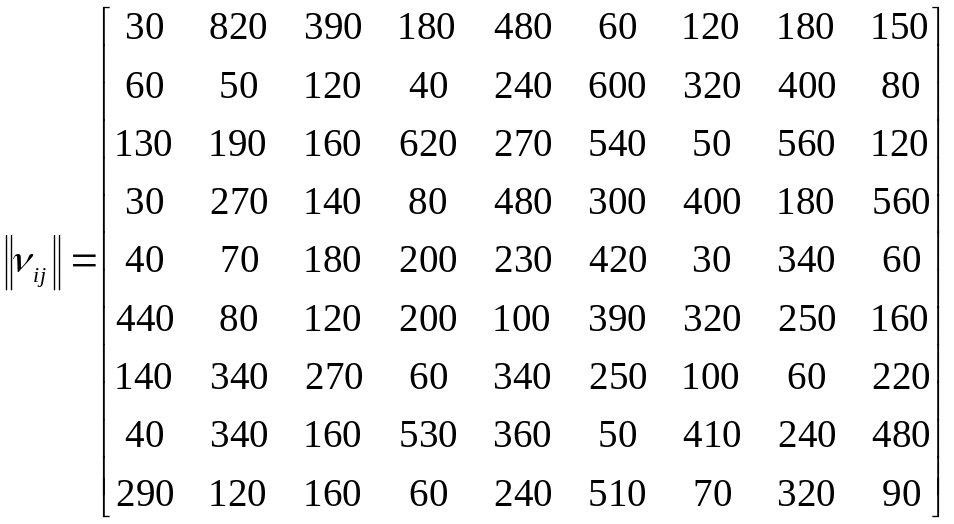
Матрица ёмкости сети V получается из матрицы сложением числа каналов _ij + _ji:

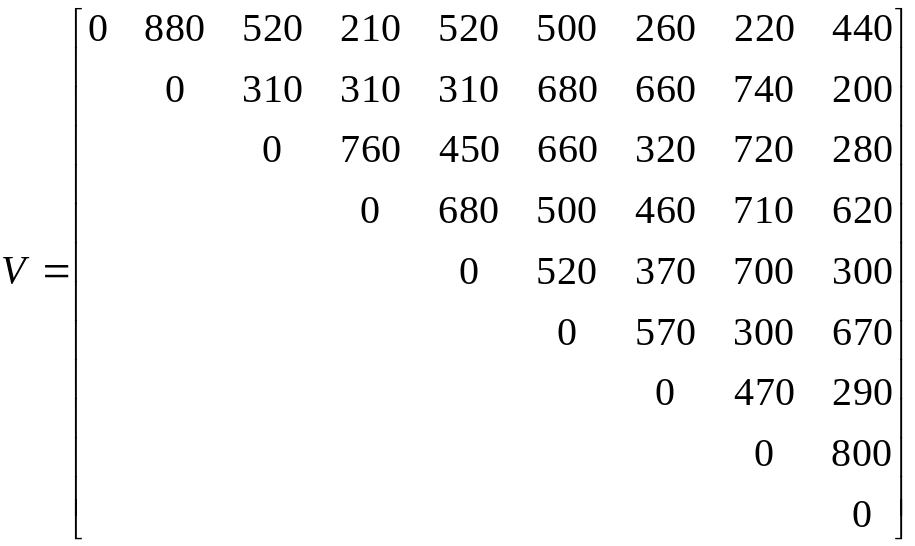
Из таблицы приложения 3 и на основании матрицы V получаем матрицу капитальных затрат:

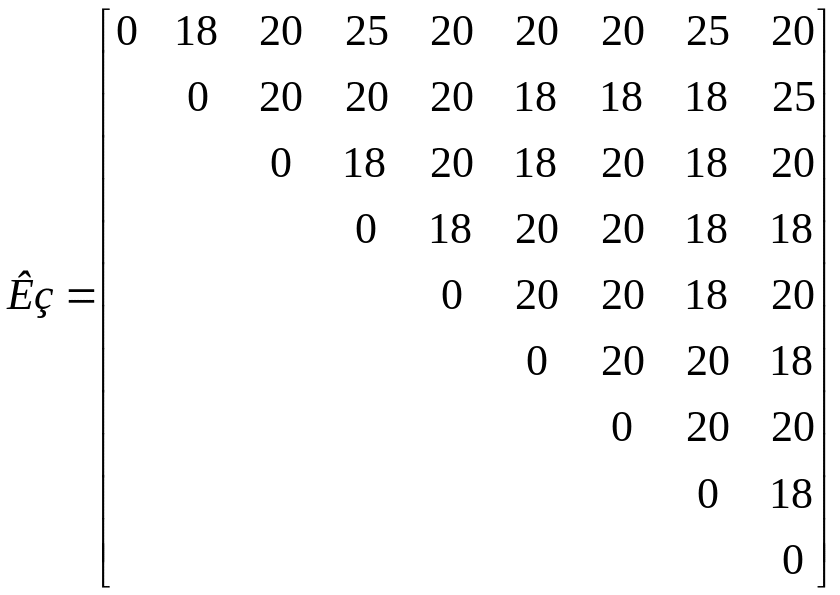
2. Расчёт сети с мпв

1. Определим структуру сети с МПВ:

Сеть с МПВ состоит из ветвей: 7-9, 5-7, 3-5, 1-3, 1-4, 2-4, 4-6, 6-8.

2. Рассчитаем суммарную протяженность сети с МПВ:

;

; ;

; ;

; ;

; ;

; ;

; ;

; ;

; ;

; ;

; ;

; ;

; ;

; ;

; .

3. Построим модель структуры сети с МПВ:

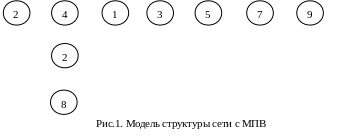
4. Построим график зависимости суммарной протяжённости ветвей сети от числа ветвей (n):

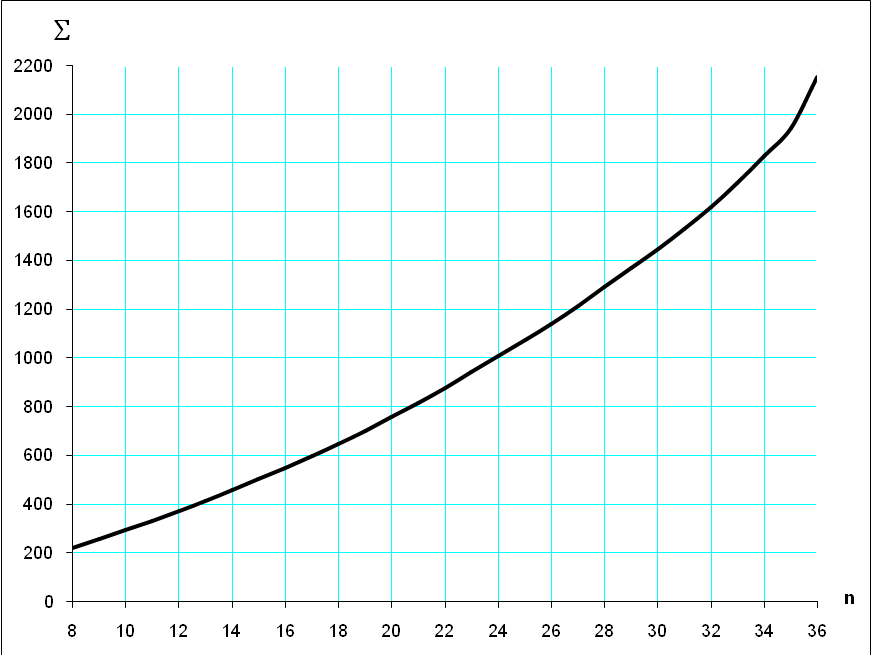
Рис. 2. Зависимость суммарной протяжённости ветвей сети от числа ветвей n

5. Вывод. С увеличением количества ветвей увеличивается и их суммарная протяжённость.

3. Расчёт сети с мпс

1. Исходные данные:

• N = 9;

• ;

• ;

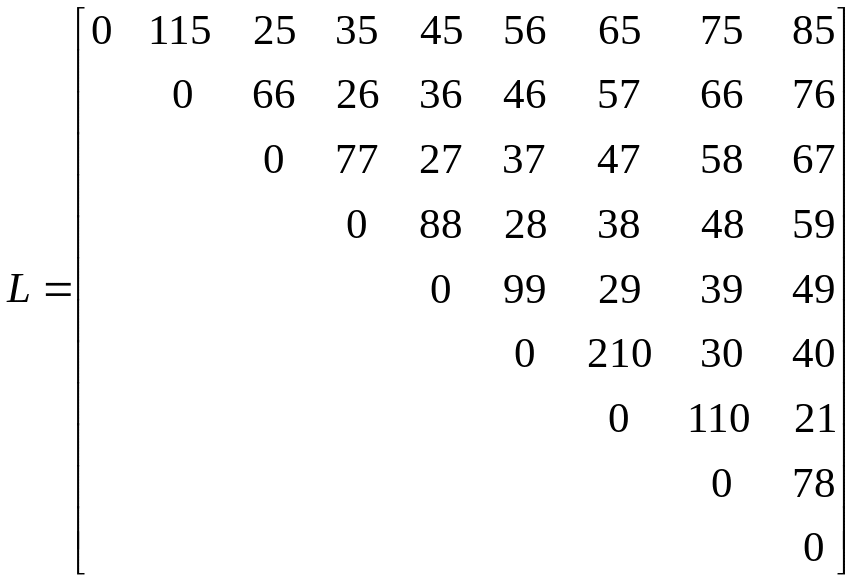• n_min = N – 1 = 8;

• .

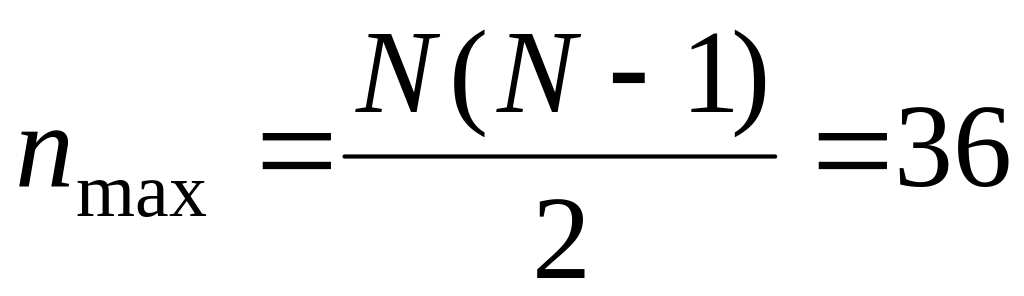2. Рассчитаем суммарную протяженность связей при n = n_max = 36:

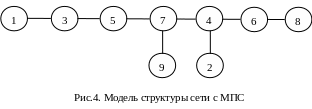
3. Построим модель структуры сети с избыточными связями.

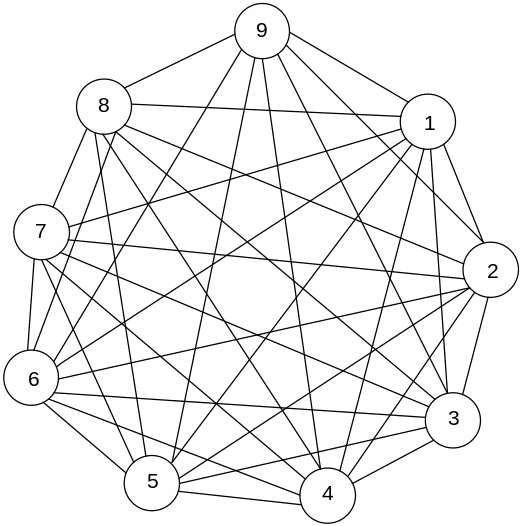
Рис. 3. Модель структуры сети с избыточными связями

4. Рассчитаем подробно суммарную протяжённость связей при n = n_max – 1 = = 35.

Возможны следующие обходы:

без ветви 1-2 кратчайший обходной путь (1-4; 4-2) L_св = 880((35 + 26) – 115) = = -47520 кан.–км;

без ветви 1-3 кратчайший обходной путь (1-5; 5-3) L_св = 24440 кан.–км;

без ветви 1-4 кратчайший обходной путь (1-6; 6-4) L_св = 10290 кан.–км;

без ветви 1-5 кратчайший обходной путь (1-3; 3-5) L_св = 3640 кан.–км;

без ветви 1-6 кратчайший обходной путь (1-3; 3-6) L_св = 3000 кан.–км;

без ветви 1-7 кратчайший обходной путь (1-3; 3-7) L_св = 1820 кан.–км;

без ветви 1-8 кратчайший обходной путь (1-3; 3-8) L_св = 1760 кан.–км;

без ветви 1-9 кратчайший обходной путь (1-7; 7-9) L_св = 430 кан.–км;

без ветви 2-3 кратчайший обходной путь (2-5; 5-3) L_св = -930 кан.–км;

без ветви 2-4 кратчайший обходной путь (2-6; 6-4) L_св = 14880 кан.–км;

без ветви 2-5 кратчайший обходной путь (2-7; 7-5) L_св = 15500 кан.–км;

без ветви 2-6 кратчайший обходной путь (2-4; 4-6) L_св = 5440 кан.–км;

без ветви 2-7 кратчайший обходной путь (2-4; 4-7) L_св = 4620 кан.–км;

без ветви 2-8 кратчайший обходной путь (2-4; 4-8) L_св = 5920 кан.–км;

без ветви 2-9 кратчайший обходной путь (2-7; 7-9) L_св = 400 кан.–км;

без ветви 3-4 кратчайший обходной путь (3-1; 1-4) L_св = -12920 кан.–км;

без ветви 3-5 кратчайший обходной путь (3-1; 1-5) L_св = 19350 кан.–км;

без ветви 3-6 кратчайший обходной путь (3-1; 1-6) L_св = 209040 кан.–км;

без ветви 3-7 кратчайший обходной путь (3-5; 5-7) L_св = 2880 кан.–км;

без ветви 3-8 кратчайший обходной путь (3-5; 5-8) L_св = 5760 кан.–км;

без ветви 3-9 кратчайший обходной путь (3-7; 7-9) L_св = 280 кан.–км;

без ветви 4-5 кратчайший обходной путь (4-2; 2-5) L_св = -17680 кан.–км;

без ветви 4-6 кратчайший обходной путь (4-2; 2-6) L_св = 22000 кан.–км;

без ветви 4-7 кратчайший обходной путь (4-9; 9-7) L_св = 19320 кан.–км;

без ветви 4-8 кратчайший обходной путь (4-6; 6-8) L_св = 7100 кан.–км;

без ветви 4-9 кратчайший обходной путь (4-7; 7-9) L_св = 0 кан.–км;

без ветви 5-6 кратчайший обходной путь (5-3; 3-6) L_св = -18200 кан.–км;

без ветви 5-7 кратчайший обходной путь (5-9; 9-7) L_св = 15170 кан.–км;

без ветви 5-8 кратчайший обходной путь (5-3; 3-8) L_св = 32200 кан.–км;

без ветви 5-9 кратчайший обходной путь (5-7; 7-9) L_св = 300 кан.–км;

без ветви 6-7 кратчайший обходной путь (6-9; 9-7) L_св = -84930 кан.–км;

без ветви 6-8 кратчайший обходной путь (6-4; 4-8) L_св = 13800 кан.–км;

без ветви 6-9 кратчайший обходной путь (6-4; 4-9) L_св = 31490 кан.–км;

без ветви 7-8 кратчайший обходной путь (7-5; 5-8) L_св = -19740 кан.–км;

без ветви 7-9 кратчайший обходной путь (7-5; 5-9) L_св = 16530 кан.–км;

без ветви 8-9 кратчайший обходной путь (8-6; 6-9) L_св = -6400 кан.–км.

Таким образом, кратчайший обходной путь (6-9; 9-7) без ветви 6-7 даёт выигрыш в L_св = 84930 кан.–км. Причина выигрыша в том, что обходной путь исключаемой ветви получается короче, чем прямой путь: 40 + 21 = 61 км вместо 210 км. В итоге имеем отрицательный прирост протяженности сетей.

Произведём перераспределение каналов в матрицах L и V:

• ;

• ;

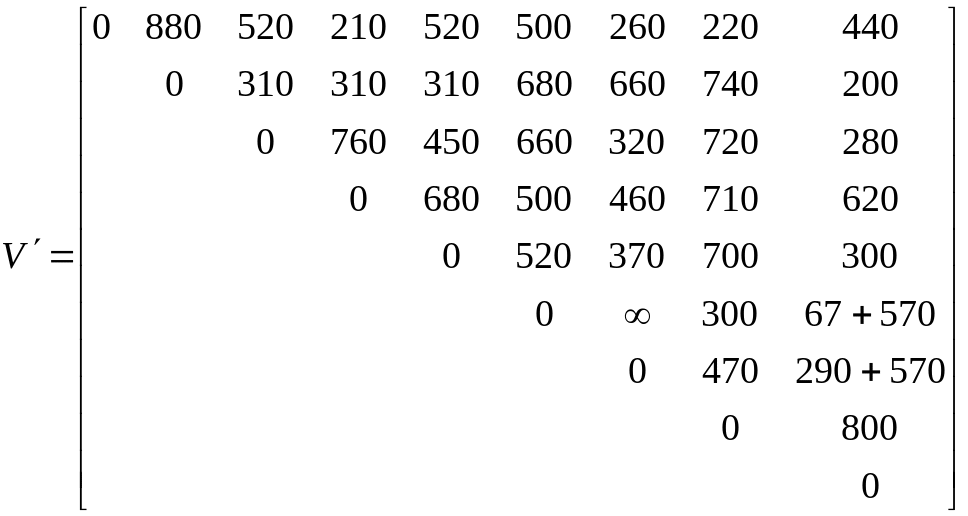Суммарная протяжённость связей составит:

Аналогично рассчитываем протяжённость связей для n = n_max – 2 = 34, n = n_max – 3 = 33 и т.д. до тех пор, пока n не станет равным n = n_min = 8.

Все итерации представим в виде таблицы:

№ итерации	n	Исключаемая ветвь	Кратчайший обходной путь	Lсв min	ПС
0	nmax = 36	–	–	–	1128900
1	35	6-7	(6-9; 9-7)	-84930	1043970
2	34	1-2	(1-4; 4-2)	-47520	996450
3	33	7-8	(7-5; 5-8)	-19740	976710
4	32	5-6	(5-3; 3-6)	-18200	958510
5	31	4-5	(4-2; 2-5)	-17680	940830
6	30	3-4	(3-1; 1-4)	-12920	927910
7	29	8-9	(8-6; 6-9)	-6400	921510
8	28	2-3	(2-5; 5-3)	-930	920580
9	27	4-9	(4-7; 7-9)	0	920580
10	26	3-9	(3-7; 7-9)	280	920860
11	25	5-9	(5-7; 7-9)	300	921160
№ итерации	n	Исключаемая ветвь	Кратчайший обходной путь	Lсв min	ПС
12	24	2-9	(2-7; 7-9)	400	921560
13	23	1-9	(1-7; 7-9)	440	922000
14	22	1-8	(1-3; 3-8)	1760	923760
15	21	1-6	(1-3; 3-6)	3000	926760
16	20	1-5	(1-3; 3-5)	3640	930400
17	19	1-7	(1-3; 3-7)	4900	935300
18	18	2-6	(2-4; 4-6)	5440	940740
19	17	2-8	(2-4; 4-8)	5920	946660
20	16	2-7	(2-4; 4-7)	6020	952680
21	15	3-8	(3-5; 5-8)	7520	960200
22	14	3-7	(3-4; 4-7)	11700	971900
23	13	4-8	(4-6; 6-8)	14500	986400
24	12	2-5	(2-4; 4-7; 7-5)	74100	1060500
25	11	3-6	(3-1; 1-4; 4-6)	85680	1146180
26	10	6-9	(6-4; 4-7; 7-9)	95880	1242060
27	9	5-8	(5-7; 7-4; 4-6; 6-8)	181460	1423520
28	8	1-4	(1-3; 3-5; 5-7; 7-4)	296520	1720040

Как можно заметить, на первых восьми итерациях сумма ПС получается меньше, чем на предыдущих итерациях. Причина в том, что обходной путь исключаемых ветвей получается короче, чем прямой путь.

Окончательный вид матриц L и V после последней итерации:

• ;

• 

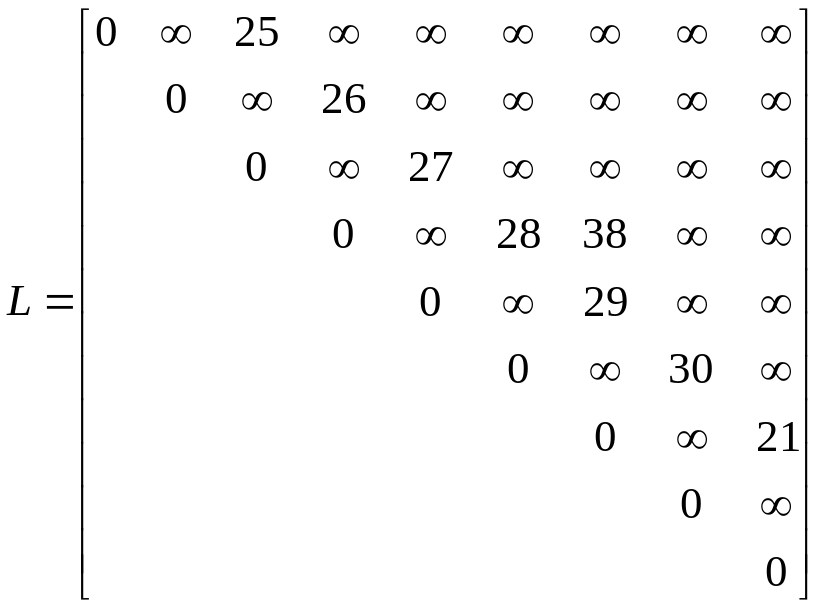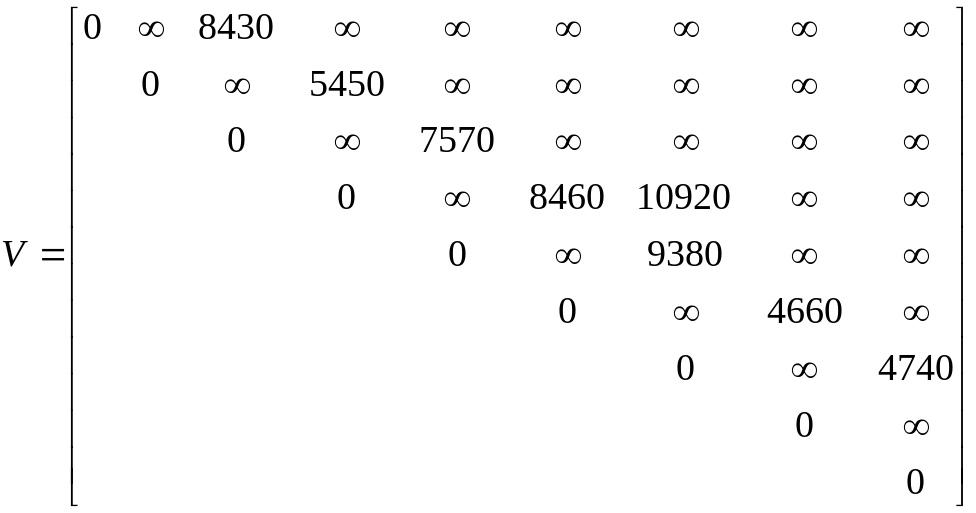
5. Построим модель структуры сети с МПС: