3.2 Применение метода состояний для устройств и систем с резервированием

Рис. 4.7. Система с дублированием

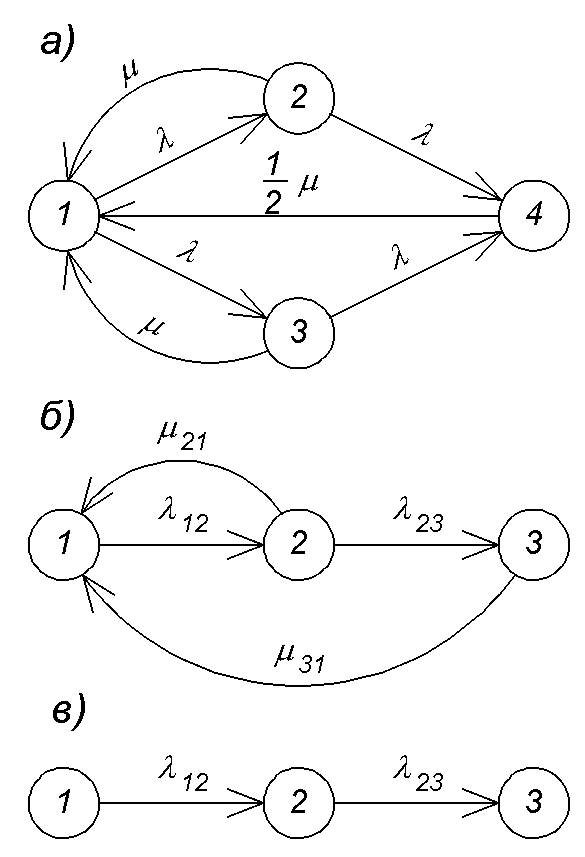
Рис.8. Графы систем с резервированием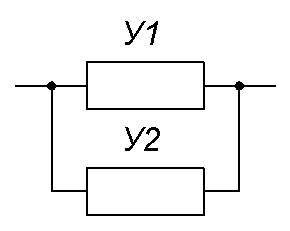

Для конкретности и наглядности иллюстрации метода ограничимся частным случаем резервирования – дублированием (рис..7). Пусть интенсивность отказа любого из устройств У1, У2 будет , а интенсивность восстановления каждого из них - . Допустим, что при отказе любого из устройств У1, У2, оно восстанавливается. Если же до момента восстановления отказавшего устройства отказывает и другое устройство, то восстанавливаются оба устройства и система в целом не функционирует пока они не будут восстановлены. С учетом сделанных предположений рассматриваемой системе отвечает граф состояний, изображенный на рис.8, а. В состоянии 1 работоспособны У1 и У2. В состоянии 2 устройство У2 работоспособно, а У1 восстанавливается. В состоянии 3 У1 работоспособно, а У2 восстанавливается. В состоянии 4 восстанавливаются У1 и У2. Учитывая симметричность, граф рис. 8, а можно упростить. При этом состояния 2 и 3 объединяются в одно, отвечающее случаю, когда отказало какое-либо одно из устройств, а другое остается исправным. Упрощенный граф состояний представлен на рис..8, б и ему отвечают, соответственно, следующие интенсивности переходов из состояния в состояние: , , , . Здесь предполагается, что при восстановлении двух отказавших ветвей интенсивность восстановления падает в два раза по сравнению с восстановлением только одной ветви, т.к. число ремонтников остается неизменным.

Опираясь на рассмотренную в п..3.1 методику, составляем систему уравнений для графа (рис.8, б):

(.27)

Для решения системы определяем начальные условия в виде , , , то есть считаем, что система исходно абсолютна исправна. Так же как и в п.4.3.2, решать систему (.27) будем с помощью операторного метода, учитывая, что

Представим.27) в операторной форме:

.28)

Найдем определитель системы (.28):

, .29)

где – элемент матрицы на пересечении -строки и -го столбца, – алгебраическое дополнение. После суммирования получим:

30)

Аналогичным образом, заменяя поочередно столбцы определителя.29) столбцом свободных членов системы (.28), получим выражения определителей:

, (.31)

, .32)

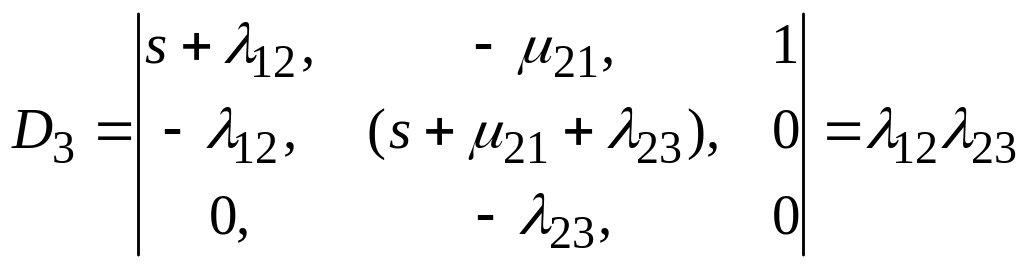. .33)

Воспользовавшись формулой Крамера, находим решение системы.28):

, , . 34)

Далее, как и в п.3.1, с помощью таблицы обратных преобразований по Лапласу] от полученных изображений переходят к оригиналам.

Перейдем от общего решения к одному важному для практики случаю, соответствующему системе с дублированием, но без восстановления. Для такой системы очевидно , и граф на рис.8, б трансформируется в граф на рис.8, в.

Определители принимают более простой вид:

а определитель остается без изменения: . Воспользовавшись.34) и принимая во внимание, что , , получаем

, (.35)

, (.36)

. .37)

Переходим от изображений 35),.36), (.37) к оригиналам:

, (.38)

, (.39)

. (.40)

Работоспособной системе отвечают состояния 1 и 2 графа рис..8, в. Следовательно, для данного случая вероятность безотказной работы системы с дублированием

, (.41)

а вероятность отказа соответственно:

. (.42)

Метод состояний может быть с успехом использован для оценки надежности сложных радиоэлектронных систем с учетом «надежности» человека-оператора. Такие системы относятся к классу человеко-машинных систем. В экстремальных ситуациях система может автоматически выполнять функции без оператора, а оператор может рассматриваться как многофункциональное резервное звено системы. На рис,9 изображен возможный граф, отображающий человеко-машинную систему. Состояние 1 графа отвечает исправной системе и работоспособному оператору. Из-за различного рода перегрузок (физических, психических и т.д.) оператор может на некоторое время утратить нормальную работоспособность, но система при этом останется исправной и будет выполнять свои функции нормально без оператора. Она даже может адаптироваться к условиям функционирования. Такой ситуации отвечает состояние 2 графа. Из этого состояния человеко-машинная система может вернуться (или не вернуться) в состояние 1 после исчезновения перегрузок. Если в системе произошел отказ, но его последствия могут быть скомпенсированы оператором (например, с помощью ручного управления, регулировки, подстройки), то в целом человеко-машинная система остается исправной и будет находиться в состоянии 3. Если имеется возможность, то через некоторое время с помощью оператора неисправность в системе может быть устранена и человеко-машинная система будет снова возвращена в состояние 1.

Рис.9. Граф человеко-машинной системы

Состояние 4 является конечным. В этом состоянии и система, и оператор неработоспособны. Предполагается, что человеко-машинная система из этого состояния не может перейти в другое. Однако это не значит, что при проектировании нельзя заложить возможности перехода человеко-машинной системы из состояния 4 в состояние 2, 3 и даже 1. Граф такой системы, естественно, будет отличаться от графа на рис.9.

Оценка вероятности безотказной работы человеко-машинной системы может быть осуществлена с использованием метода состояний.