
Оценка надежности электронных устройств и систем сложной структуры .1. Метод свертки
В общем случае радиоэлектронные устройства и системы с резервированием представляют собой сложные последовательно-параллельные структуры. При расчете надежности таких устройств используют метод, позволяющий перейти к структуре последовательно соединенных элементов. Метод основан на замене нескольких параллельно соединенных элементов структуры одним элементом с эквивалентной надежностью учитывающей параллельность соединения. Таким образом, сложная структура «сворачивается» постепенно в простую последовательную структуру. Поэтому такой метод и называется методом свертки.
Проиллюстрируем
метод с помощью сворачивания структуры,
изображенной на рис..1,
а.
Обозначим вероятности безотказной
работы структурных элементов У1,
У2, …, У11 за некоторое время t,
как
![]() ,
а вероятности их отказов
,
а вероятности их отказов
![]() соответственно.
Выделим узлы, состоящие из параллельно
соединенных элементов: узел
1 - элементы
УЗ, У4, У5; узел
2 - элементы
У7, У8; узел
3 - элементы
У9, У10,
У11.
Найдем вероятности отказа, этих узлов:
соответственно.
Выделим узлы, состоящие из параллельно
соединенных элементов: узел
1 - элементы
УЗ, У4, У5; узел
2 - элементы
У7, У8; узел
3 - элементы
У9, У10,
У11.
Найдем вероятности отказа, этих узлов:
![]() .
.
Вероятность их безотказной работы соответственно будет:
![]() .
.
Рис.1.
Принцип сворачивания структуры системы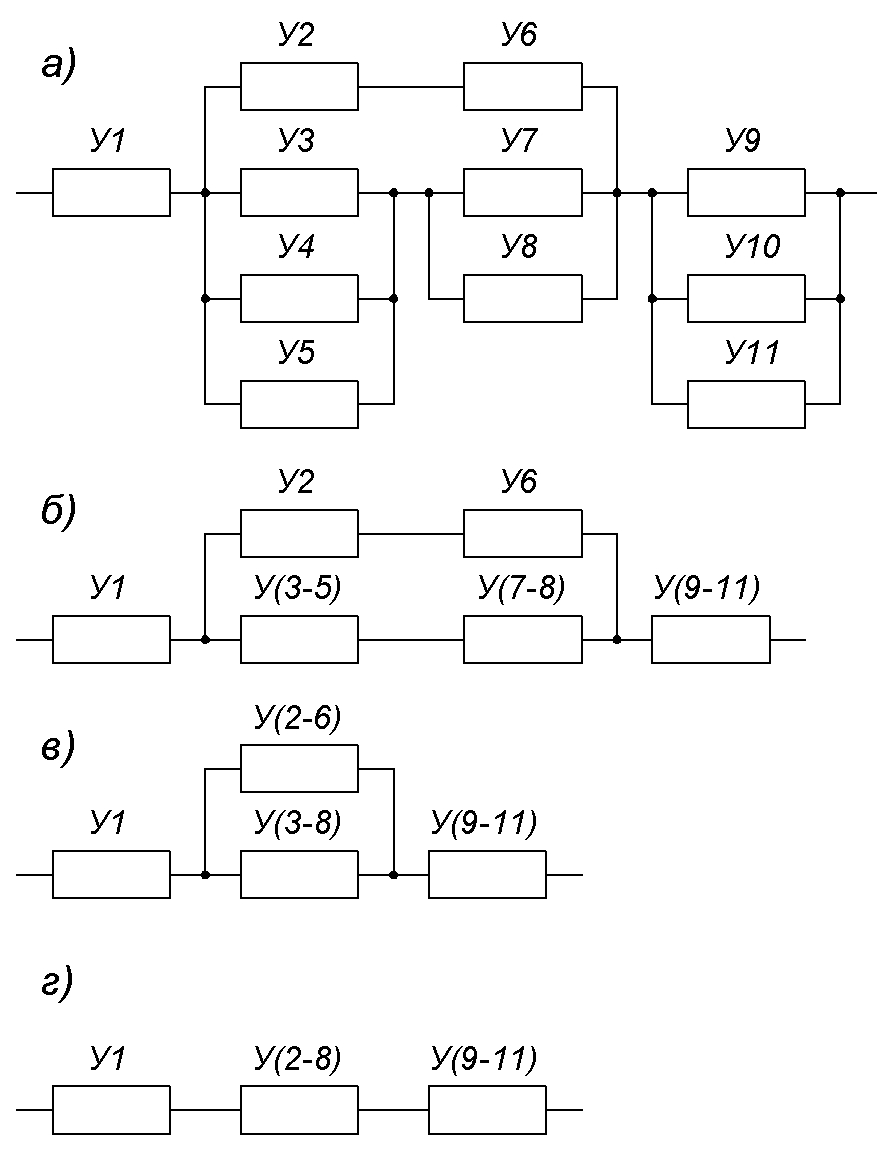
![]() .
Трансформированная структура изображена
на рис..1,
б.
Она содержит один узел, состоящий из
двух параллельных ветвей. Ветвь
1 - элементы
У2,
У6, ветвь
2 - элементы
У(3-5),
У(7-8).
Вероятности безотказной работы этих
ветвей:
.
Трансформированная структура изображена
на рис..1,
б.
Она содержит один узел, состоящий из
двух параллельных ветвей. Ветвь
1 - элементы
У2,
У6, ветвь
2 - элементы
У(3-5),
У(7-8).
Вероятности безотказной работы этих
ветвей:
![]() ;
;
![]() ,
,
а вероятности отказа:
![]() ;
;
![]() .
.
Осуществим
вторую свертку, заменяя ветвь
1
и ветвь
2 эквивалентами
с вероятностями отказа
![]() .
В новой структуре (рис..1,
в)
имеется лишь один узел, вероятность
отказа которого
.
В новой структуре (рис..1,
в)
имеется лишь один узел, вероятность
отказа которого
![]() ,
,
а вероятность безотказной работы соответственно
![]() .
.
Осуществляем
третью свертку, заменяя узел У(2-6),
У(3-8)
эквивалентом
с вероятностью безотказной работы
![]() .
В результате приходим к простой
последовательной структуре (рис..1, г).
Таким образом, вероятность
безотказной работы системы
с исходной структурой (рис..1,
а)
может быть определена как
.
В результате приходим к простой
последовательной структуре (рис..1, г).
Таким образом, вероятность
безотказной работы системы
с исходной структурой (рис..1,
а)
может быть определена как
![]() ,
,
а вероятность отказа соответственно
![]() .
.
В некоторых случаях не удается непосредственно с помощью метода свертки перейти к простой последовательной структуре. Это относится к сложным структурам с перекрестными связями. Для них применяют другие методы, рассматриваемые далее.
.2. Логико-вероятностный метод
В ряде случаев, устройство или систему невозможно представить структурно состоящей из параллельно-последовательных соединений. Особенно это относится к цифровым электронным информационным системам, в которых для повышения надежности вводятся перекрестные информационные связи. На рис.2 изображена часть структуры системы с перекрестными связями (стрелки показывают возможные направления перемещения информации в системе). Для оценки надежности структур с перекрестными связями действенным оказывается логико-вероятностный метод.
Рис.2.
Система с перекрестными связями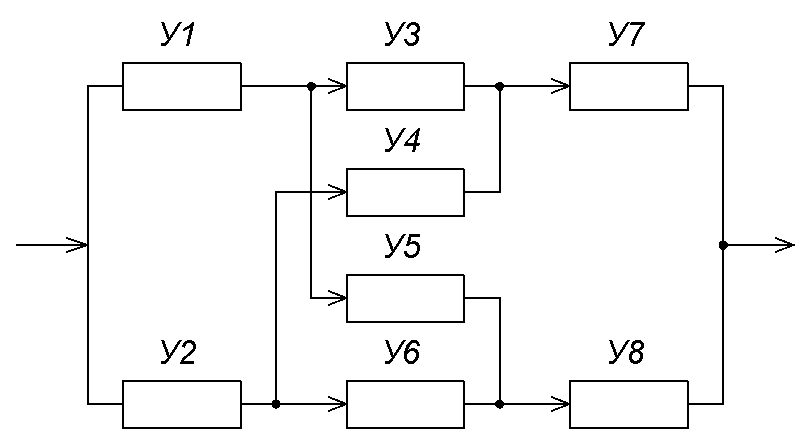
![]() обозначают событие, заключающееся в
том, что данный
обозначают событие, заключающееся в
том, что данный
![]() -й
элемент структуры работоспособен.
Формально работоспособное состояние
всей системы или устройства отображается
логической функцией, называемой функцией
работоспособности. Для нахождения этой
функции необходимо определить, следуя
от входа к выходу структуры системы,
все пути движения информации, отвечающие
работоспособному состоянию системы.
-й
элемент структуры работоспособен.
Формально работоспособное состояние
всей системы или устройства отображается
логической функцией, называемой функцией
работоспособности. Для нахождения этой
функции необходимо определить, следуя
от входа к выходу структуры системы,
все пути движения информации, отвечающие
работоспособному состоянию системы.
Например, для структуры рис..2 таких путей – четыре. Путь 1-У1У3У7. Путь 2-У1У5У8. Путь 3-У2У6У8. Путь 4-У2У4У7.
Зная все пути, отвечающие работоспособному состоянию структуры, нетрудно записать в символах алгебры логики в дизъюнктивно-конъюиктивной форме функцию работоспособности.
Например, для рис..2 функция работоспособности
![]()
Применяя известные методы минимизации, логическую функцию работоспособности (если имеется возможность) упрощают и переходят от нее к уравнению работоспособности системы в символах обычной алгебры. Осуществляется такой переход формально с использованием известных соотношений (слева логическая запись, справа – алгебраическая):
![]() , (.1)
, (.1)
![]() , (.2)
, (.2)
![]() . (3)
. (3)
Вероятность
безотказной работы устройства или
системы в целом определяется формальной
подстановкой в алгебраическое выражение
функции работоспособности вместо
переменных
значений вероятностей безотказной
работы
![]() каждого
-гo
элемента структуры.
каждого
-гo
элемента структуры.
Проиллюстрируем применение логико-вероятностного метода на двух примерах.
Пример
1.
Найдем в общем виде вероятность
безотказной работы устройства, структура
которого представлена на рис..3. Для
наглядности проинтерпретируем назначение
элементов структуры. Элементы У1, У2 –
два одинаковых равнонадежных запоминающих
устройства (ЗУ) с вероятностью безотказной
работы
![]() .
Элементы У3, У4 – два одинаковых
равнонадежных процессора с вероятностью
безотказной работы
.
Элементы У3, У4 – два одинаковых
равнонадежных процессора с вероятностью
безотказной работы
![]() .
Элемент У5 – блок, обеспечивающий
двустороннюю передачу цифровых данных.
Вероятность безотказной работы этого
блока -
.
Элемент У5 – блок, обеспечивающий
двустороннюю передачу цифровых данных.
Вероятность безотказной работы этого
блока -
![]() .
.
Рис.3.
Мостиковая структура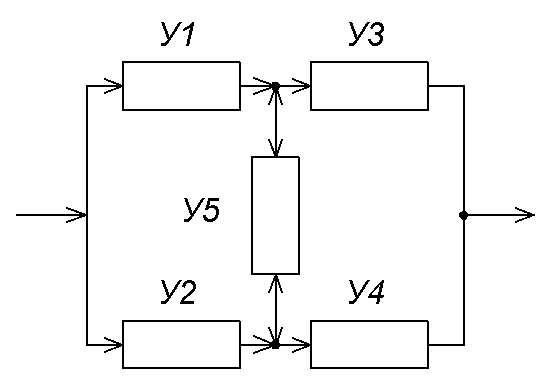
У1У3 или У1У5У4 или У3У4
или У2У5У3. (.3)
Перейдем от (4.3) к функции работоспособности в символах алгебры логики:
![]() . (.4)
. (.4)
Учитывая (1), (.2), (.3), осуществляем формальный переход от записи (.4) к алгебраической форме записи:
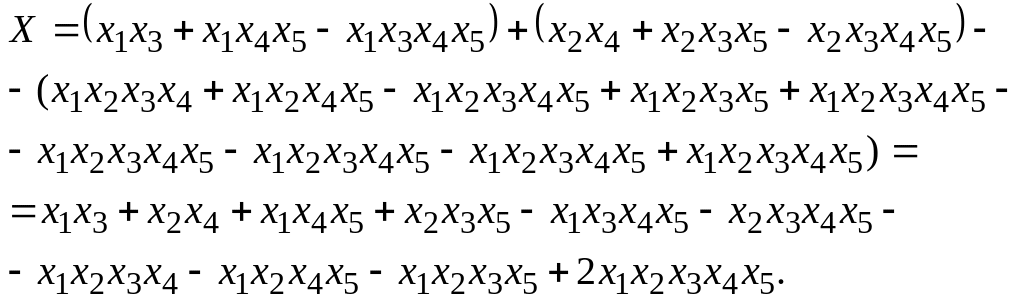 (.5)
(.5)
От
(.5) переходим к вероятности безотказной
работы всего устройства путем формальной
замены
на
.
При этом, опуская аргумент
![]() и принимая во внимание, что
и принимая во внимание, что
![]() и
и
![]() ,
получим окончательно:
,
получим окончательно:
![]() .
.
Пример
2.
Применим логико-вероятностный метод
для оценивания вероятности безотказной
работы устройства с раздельным
резервированием (рис.4). Пусть исходно
задано, что все элементы устройства
равнонадежны и обладают вероятностью
безотказной работы
![]() .
Запишем функцию работоспособности
устройства в символах алгебры логики:
.
Запишем функцию работоспособности
устройства в символах алгебры логики:
![]() .
.
Переходим к традиционной алгебраической форме записи:
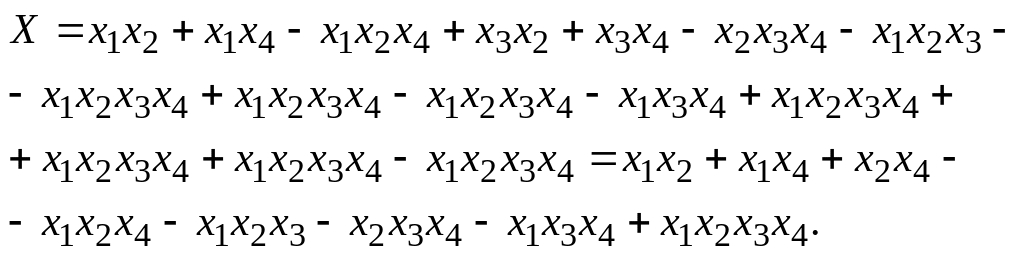
Рис4.
Система с раздельным дублированием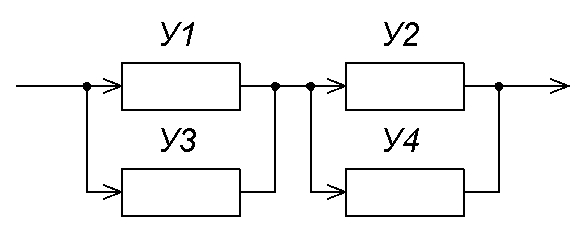
![]() .
.
Применим для этого же примера метод свертки. Рассматриваемое устройство имеет два узла из параллельно соединенных элементов. Вероятность безотказной работы узла из элементов У1, У3:
![]() .
.
Вероятность безотказной работы узла из элементов У2, У4:
![]() .
.
Вероятность безотказной работы всего устройства:
![]()
или
![]() .
.
Как и следовало ожидать, результат получился таким же, как и при применении логико-вероятностного метода.
