25.Вероятностный подход к измерению количества информации.

При вероятностном подходе предполагается, что существует обратная зависимость между величиной информации, содержащейся в сообщении о каком-либо событии и вероятностью осуществления этого события.

Пусть имеется алфавит, состоящий из m символов. Как измерить количество информации (I), которое можно передать при помощи этого алфавита?

Было предложено принять в качестве меры количества информации число сообщений (N), которое можно передать при помощи этого алфавита. Например, пусть алфавит состоит из двух символов: а и b (m = 2). Сообщение может содержать разное число символов (n).

Хартли (1928 г.) предложит измерять информацию, приходящуюся на одно сообщение, логарифмом числа сообщений: I = log N.

Таким образом, общее количество информации будет равно

I = log N = log m" = n • log m, где m – количество вариантов информации

Далее Хартли предположил, что вероятность появления любого символа из алфавита одинакова и равна р = 1 / т. Тогда общее количество информации можно выразить через вероятность появления символов з сообщении

I = п • log m = n ■ log (1 / p) = - n • log p.

Количество информации, приходящееся на один символ будет равно

I = - log р.

Для использования этой формулы на практике необходимо задать единицу измерения количества информации, которым выступает бит.

Формулу Хартли можно применять только в случае одинаковой вероятности появления символов. Однако, это не всегда уместно. Поэтому Шеннон (1948 г.) предложил другую формулу:

где pi - вероятность появления i-ro символа в сообщении. В данном случае Н - это среднее количество информации, приходящееся на один символ.

Формула Хартли является частным случаем формулы Шеннона. Если

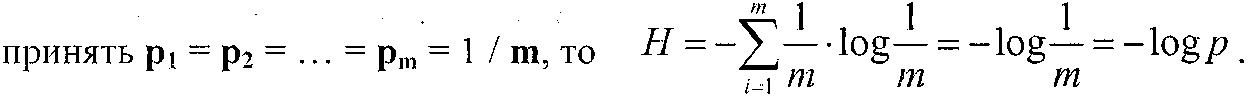
Величину Н называют энтропией Шеннона. В теории информации энтропия - это мера неопределенности ситуации.

Чем больше энтропия системы, тем больше степень ее неопределенности. Поступающее сообщение полностью или частично снимает эту неопределенность. Следовательно, количество информации можно измерять тем, насколько понизилась энтропия системы после поступления сообщения.

26.Смысловой подход к измерению количества информации.

В рамках смыслового выделяют семантический и прагматический подходы.

При семантическом подходе пытаются измерить смысловое содержание сообщений.

Пусть поступили два сообщения:

Дважды два - четыре.

Совершенно незнакомая математическая формула.

Первое сообщение можно выразить словами «известно все», а второе - «неизвестно ничего». Информация была передана, мы ее получили, но обнаружить ее невозможно.

Таким образом, при семантическом подходе, количество полученной информации предлагается измерять степенью изменения знаний того, кто ее получил. Чем больше изменились знания получателя сообщения, тем большее количество информации содержит сообщение.

Другой вопрос - как измерить степень изменения знаний получателя. Одной из попыток описания этого процесса является модель Шрейдера.

В основе модели Шрейдера лежит понятие тезауруса.

Тезаурус (греч. - сокровище) - это знания человека, представленные в виде понятий и отношений между ними, т.е. определенным образом структурированное знание. Утверждается, что человек извлечет информацию из сообщения, только в том случае, если изменится его тезаурус. Причем, чем сильнее изменения, тем больше информации.

Рассмотрим - как модель Шрейдера объясняет процесс передачи информации. Пусть источник сообщения - преподаватель, а получатель -студент. И у преподавателя и у студента есть свой тезаурус. Преподаватель на лекции сообщает студенту какие-то знания, т.е. фрагмент своего тезауруса. Возможны три ситуации.

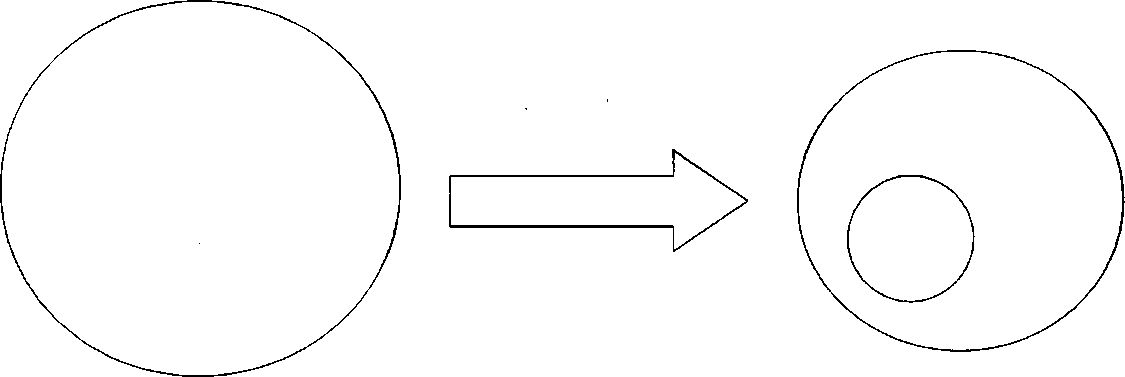
1) Сообщение полностью известно студенту (дважды два - четыре). Графически это можно представить как полное вхождение фрагмента тезауруса преподавателя (маленький круг) в тезаурус студента (рис.). Это ситуация «известно все». Тезаурус студента не изменяется и передачи информации не происходит.

2) Сообщение совершенно не понятно студенту (незнакомая математическая формула). Это значит, что фрагмент содержит понятия и отношения между ними, которых нет в тезаурусе студента (рис.). Это ситуация «неизвестно ничего». Как и в первом случае передачи информации не происходит.

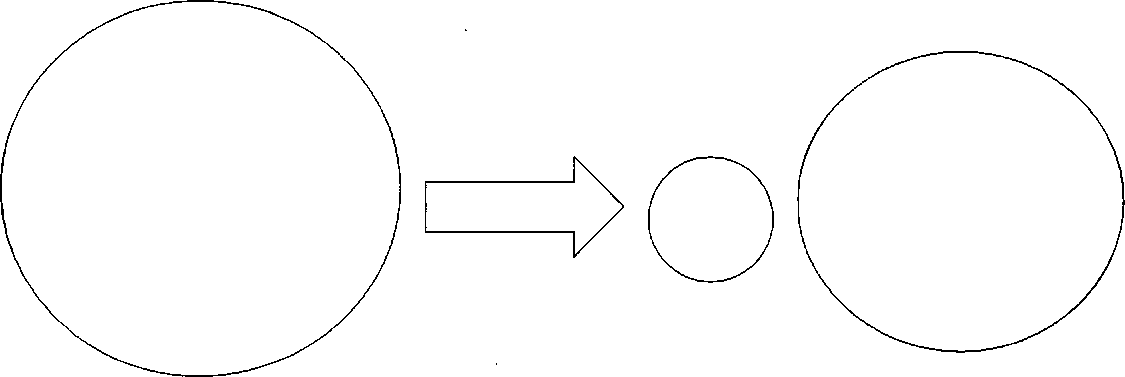
Тезаурус преподавателя Тезаурус студента

3) Фрагмент тезауруса преподавателя содержит часть понятий и отношений, которые есть в тезаурусе студента (заштрихованная область). Эта общая область играет важную роль в коммуникациях (процессах передачи знаний - обучении).

Тезаурус студента изменится и он получит информацию только в том случае, если неизвестные ему понятия и отношения можно выразить через уже имеющиеся (заштрихованная область). Если это не удается, то ввести новое понятие в тезаурус и изменить его невозможно. Таким образом, «непонятное» необходимо объяснять через «понятное».

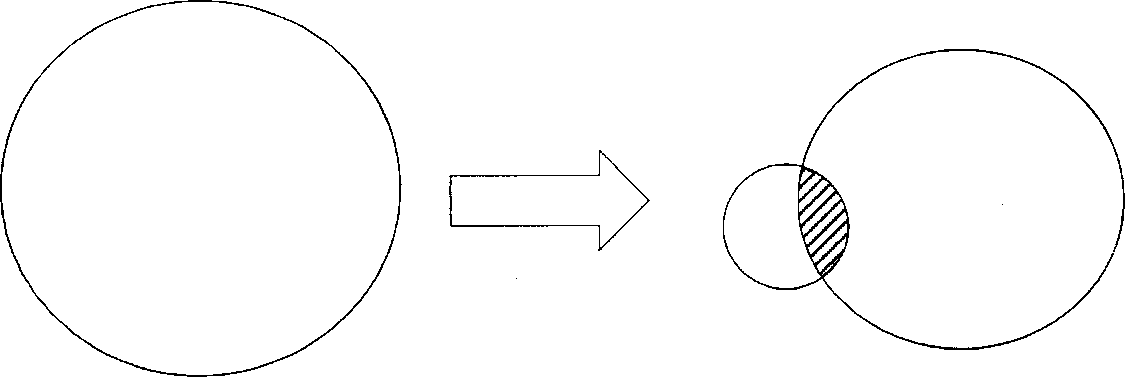
Зависимость кол-ва полученной из сообщения информации от величины тезауруса можно представить. следующим образом. (рис)

При минимальном тезаурусе (точка min) нельзя будет извлечь из сообщения информацию - „неизвестно ничего". При максимальном размере тезауруса (точка max) также не будет получена информация -„известно все". И, наконец, существует такой размер тезауруса, при котором будет получено максимум информации (точка opt).