Расстояние от данной точки до данной прямой

Расстояние d от точки М₀ (x₀; у₀; z₀) до плоскости

Ах + Ву + Сz + D = 0:

d = .

Расстояние d от точки М₀ до плоскости

x cosα + y cosβ + z cosγ – p = 0:

d = | х₀ cos α + у₀ cosβ + z₀ cosγ – p |.

Пример 19. Составить уравнение плоскости, проходящей через точку

М (1, -3, -2 ) параллельно плоскости 3x – 2y + 4z – 3 = 0.

• Ищем уравнение плоскости в виде Аx + Вy + Сz + D = 0. Две параллельные плоскости имеют общую нормаль. Координаты нормали заданной плоскости

n = { 3; –2; 4 }. Следовательно, уравнение искомой плоскости имеет вид

3x – 2y + 4z + D = 0. Точка М (1, –3, –2 ) по условию лежит в искомой плоскости. Следовательно, подстановкой координат М в уравнение плоскости получим тождество: 3  1 – 2  (–3) + 4  (–2) + D = 0  D = –1  уравнение искомой плоскости имеет вид 3x – 2y + 4z – 1 = 0.

Пример 20. Найти величину острого угла между плоскостями:

а) 11х – 8у – 7z – 15 = 0 и 4х – 10у + z – 2 = 0;

б) 2х + 3у – 4z + 4 = 0 и 5х – 2у + z – 3 = 0.

• а) cos φ = = =

= = => φ = .

б) выполняется условие перпендикулярности плоскостей A₁ А₂ + B₁B₂ + C₁C₂ = 0, т.к. 2 · 5 + 3 · (-2) – 4 · 1 = 0. Следовательно, плоскости взаимно перпендикулярны => φ = .

Пример 21. Написать уравнение плоскости, параллельной плоскости

х – 2у + 2z + 5 = 0 и удаленной от точки М ( 3, 4, -2 ) на расстояние d = 5.

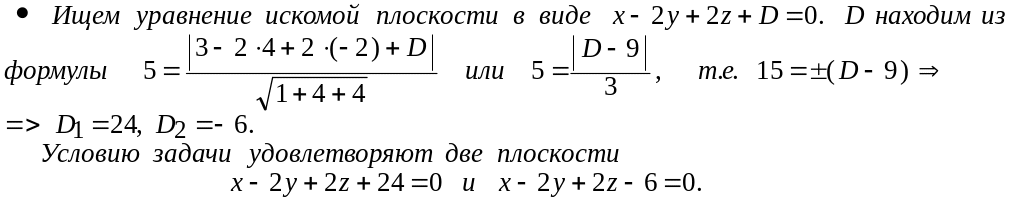
Пример 22. Составить уравнение плоскости, проходящей через точки

М ₁ (–1, 3, 0 ) и М ₂ ( 2, 4, –1 ), перпендикулярно плоскости х – 2у + 3z – 10 = 0.

2. П рямая в пространстве Различные виды уравнения прямой в пространстве

1. К анонические уравнения прямой,

п роходящей через данную точку (x₀; у₀; z₀)

п араллельно вектору = {m, n, p}:

Всякий ненулевой вектор, параллельный данной прямой, называется направляющим вектором этой прямой. Здесь направляющий вектор = {m, n, p}. Обращение в нуль одного из знаменателей означает обращение в нуль числителя:

 .

2. Параметрические уравнения прямой, проходящей через

данную точку (x₀; у₀; z₀) параллельно вектору = {m, n, p}:

,

где t – переменный параметр, t R.

3. Уравнения прямой, проходящей через две точки

М₁(x₁; у₁; z₁) и М₂(x₂; у₂; z₂):

.

4. Общее уравнение прямой задается как линия пересечения плоскостей А₁х + В₁у + С₁z + D₁ = 0 и А₂х + В₂у + С₂z + D₂ = 0.

Направляющий вектор этой прямой может быть найден как векторное произведение нормальных векторов = {A₁; B₁; С₁} и

= {A₂; B₂; С₂} этих плоскостей: = [ , ] или

= , т.е. = .

Замечание. Каноническое уравнение прямой можно получить, зная две точки этой прямой. В качестве этих точек можно взять два любых решения системы уравнений (общего уравнения прямой). Например, и . Тогда уравнение прямой, проходящей через две точки, запишется в виде:

, т.е. , или .

Направление прямой задает вектор = {4, 7, 6}. Он образует с координатными осями углы α, β и γ соответственно: