4. Уравнение прямой, проходящей через данную точку в

данном направлении:

y – y₀ = k (x – x₀)

k = tg α (α – угол, образуемый прямой с осью Ох); (x₀; у₀) – координаты данной точки.

5. Уравнение y – y₀ = k (x – x₀) называют также уравнением пучка прямых с центром в точке (x₀; у₀).

Уравнением пучка прямых, проходящих через точку пересечения двух прямых А₁х + В₁у + С₁ = 0 и А₂х + В₂у + С₂ = 0 имеет вид:

А₁х + В₁у + С₁ + λ ( А₂х + В₂у + С₂ ) = 0,

где λ – числовой множитель.

6. Уравнение прямой, проходящей через две данные точки

М₁(x₁; у₁) и М₂(x₂; у₂) :

Если x₁= x₂, то уравнение будет иметь вид: x = x₁; если у₁= у₂, то у = у₁.

6. Нормальное уравнение прямой:

x cosα + y sinα – p = 0,

где р – длина перпендикуляра, опущенного из начала

координат на прямую, α – угол, который этот перпендикуляр образует с положительным направлением оси Ох.

Общее уравнение прямой можно преобразовать в нормальное уравнение путем умножения на нормирующий множитель ; знак берется противоположным знаку свободного члена С (в общем уравнении прямой).

6. У равнение прямой в полярных координатах:

r cos (φ – α) = p.

Пример 3. Построить прямую, заданную уравнением 2х – у – 4 = 0.

• 1. Для построения построения прямой достаточно знать

координаты двух ее произвольных точек. Полагая в уравнении

прямой, например, х = 0, получим у = –4. Имеем одну точку

А (0; –4). Полагая х = 1, получим у = –2. Отсюда вторая

точка В (1; –2). Осталось построить точки А и В и провести

и провести через них прямую.

2. Задачу можно решить иначе, используя уравнение прямой

в отрезках. Для этого перенесем свободный член (–4) в правую

часть уравнения и разделим обе его части на 4. Получим

– = 1 или + = 1 – уравнение прямой в отрезках на

осях. На оси Ох отложим 2 единицы вправо (от начала координат);

на оси Оу отложим 4 единицы вниз. Получаем две точки на осях, через

которые проводим прямую.

Пример 4. Уравнение прямой 4х – 3у + 12 = 0 представить в различных видах (с

угловым коэффициентом, в отрезках, в виде нормального уравнения).

• Для получения уравнения прямой с угловым коэффициентом разрешим данное уравнение относительно у. Получим 3у = 4х + 12 и далее у = х + 4 – уравнения прямой с угловым коэффициентом; здесь k = , b = 4.

Для получения уравнения прямой в отрезках перенесем свободный член С = 12 вправо и разделим обе части уравнения на –12. В результате получим

+ = 1 – уравнения прямой в отрезках: здесь а = –3, b = 4.

Для приведения исходного уравнения к нормальному виду умножим обе его части на нормирующий множитель λ = , т.е. λ = – . Перед корнем взят знак «–», т.к. свободный член (С = 12) имеет знак «+». Получим

– (4х – 3у + 12) = 0, т.е. – х + у – = 0; здесь cos α = – , sin α =

(cos² α + sin² α = + = 1). р = , т.е. расстояние от начала координат

О (0; 0) до прямой равно 2,4.

Пример 5. Написать уравнение прямой, проходящей через точки:

а) А (0; 2), В (–3; 7) ; б) А (2; 1), В (4; 1).

• Уравнение прямой, проходящей через две точки

(х₁; у₁) и (х₂; у₂):

= .

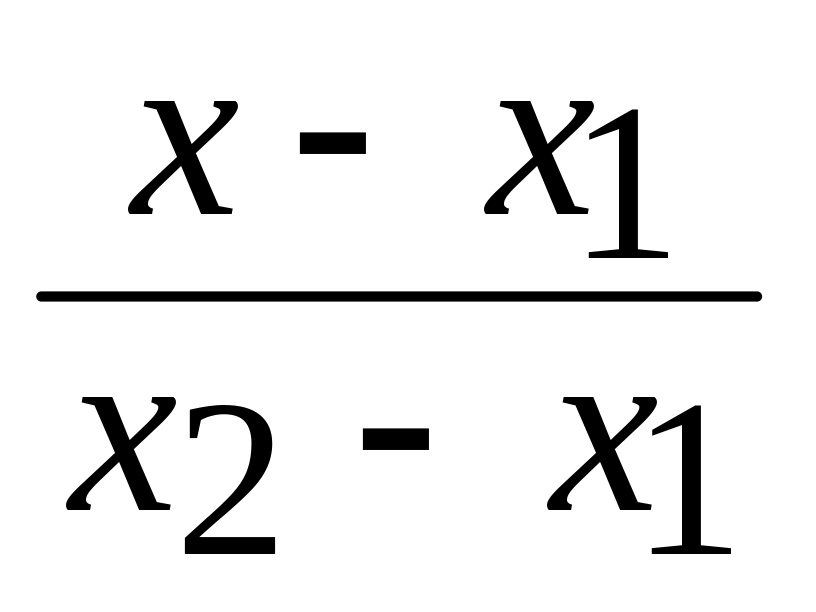а) =  =  –3y + 6 = 5x  5x + 3y – 6 = 0.

б) =  = => y – 1 = 0  y = 1.

Пример 6. Найти прямую, проходящую через точку пересечения двух прямых

–4х + 2у + 1 = 0 и х – 3у + 2 = 0 и проходящую через точку А (1; 0).

• Все прямые, проходящие через точку пересечения двух прямых –4х + 2у + 1 = 0 и х – 3у + 2 = 0, принадлежат пучку прямых –4х + 2у + 1 + λ ( х – 3у + 2 ) = 0. Подставим в уравнение пучка координаты точки А :

–4  1 + 2  0 + 1 + λ ( 1 – 3  0 + 2 ) = 0 => λ = 1.

Следовательно, уравнение искомой прямой, принадлежащей пучку и проходящей через точку А (1; 0) –4х + 2у + 1 + 1 ( х – 3у + 2 ) = 0  –3х – у + 3 = 0  3х + у – 3 = 0.

Пример 7. Составить уравнение прямой в полярных координатах, если известно, что она проходит через точку М (2; ) и наклонена к полярной оси под углом π.

• Уравнение прямой в полярных координатах

r cos (φ – α) = p (см. рис.)

См. рис.: α = – (π – π ) = – = . Тогда

р = 2 cos ( – ) = 2 cos = 2  = , т.е. р = .

Следовательно, уравнение искомой прямой: r cos (φ – ) = .