2. Середня гармонічна та середня прогресивна. Структурні середні величини.

Середня - це узагальнююча кількісна характеристика ознаки у статистичній сукупності. Вона виражає характерну типову величину варіюючої ознаки одиниць сукупності, яка утворюється в певних умовах місця і часу під впливом сукупності чинників.

Середня гармонійна - застосовують тоді, коли відсутні безпосередні дані про вагу, а відомі варіанти ознаки, що усереднюється (х), і добутки значень варіантів на кількість одиниць, які мають значення w (w = Xf). Розраховують на основі зворотних значень ознаки

Формула середньої гармонійної зваженої: ,

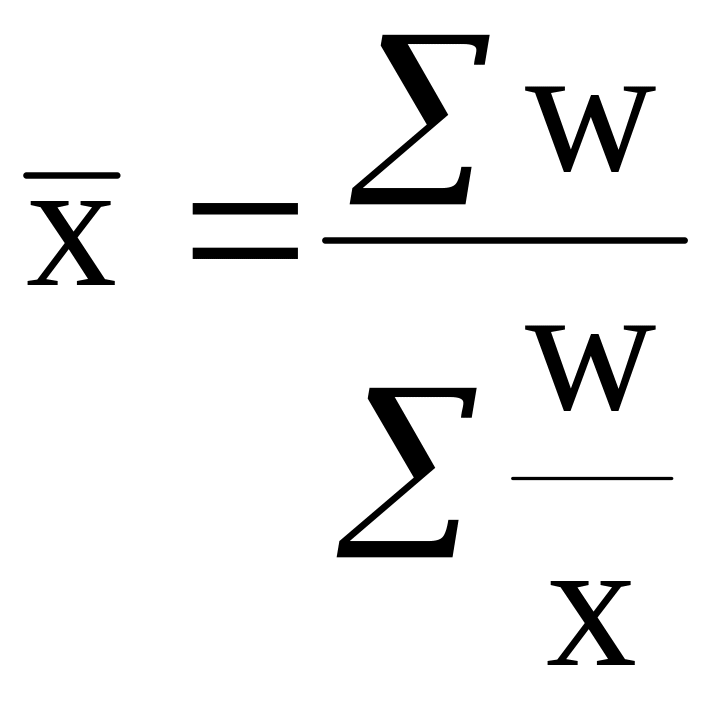Середня гармонійна проста: ,

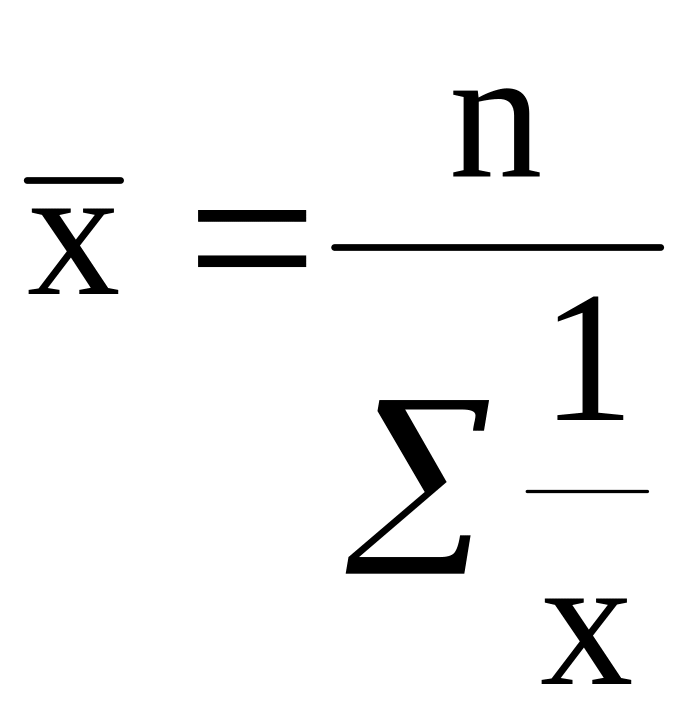де w - вага ознаки,

х - варіанти,

n - кількість членів ряду,

У ряді розподілу крім типового рівня ознаки, характеристикою якого є середня величина, важливе значення мають структурні середні величини, які характеризують структуру аналізованих сукупностей, -мода (Мо) і медіана (Me).

Мода - значення ознаки, що найбільш часто зустрічається у одиниць сукупності. Для дискретних рядів це варіант, що має найбільшу частоту.

Якщо має місце інтервальний ряд з рівними інтервалами, то мода розраховується за формулою: , де

-мода;

- початок (нижня межа) модального інтервалу, тобто інтервалу, що має найбільшу чисельність;

d - величина модального інтервалу;

- частота інтервалу, попереднього модальному;

- частота модального інтервалу;

- частота наступного за модальним інтервалу.

Медіаною - в статистиці називається варіант, що ділить чисельність ранжированого ряду (значення ознаки розташовані в порядку збільшення або зменшення значень ознаки) на дві рівні частини.

Наприклад, денний виробіток п’ятьох працюючих становить 20, 22, 24, 25, 26 грош.од. Медіана цього ряду значень дорівнює третьому варіанту, тобто 24 грош.од.

Коли ряд має парне число членів, медіаною буде середня арифметична з двох варіантів, розташованих в середині.

Маємо дані про денний виробіток 6-ох робітників: 30, 26, 25, 24, 23, 20.

Медіана буде рівною середній арифметичній з третього та четвертого варіантів: грош.од.

Порядковий номер медіани дискретного варіаційного ряду визначається таким чином: чисельність ряду збільшується на одиницю і ділиться навпіл:

В інтервальних рядах після визначення порядкового номеру медіани, за накопиченими частотами знаходиться медіанний інтервал, а після цього медіана визначається за формулою: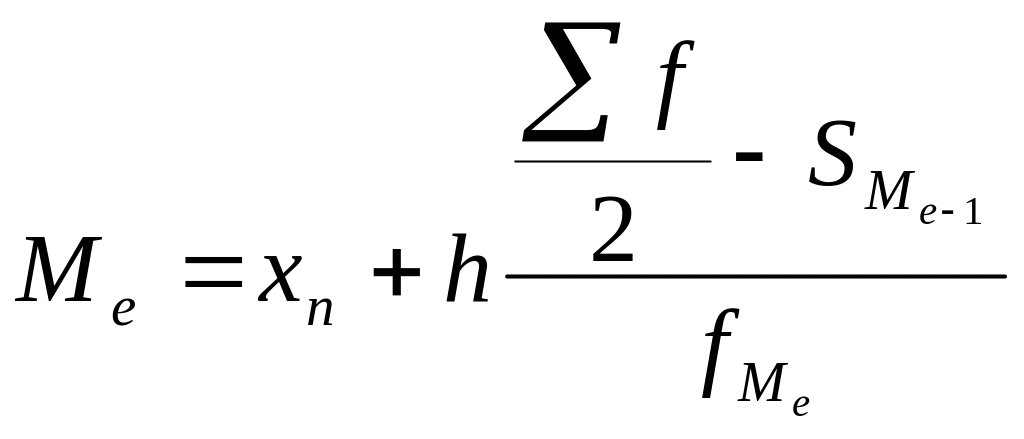 , де

- нижня границя медіанного інтервалу,

h - величина інтервалу медіанного,

- порядковий номер медіани,

- частота, накопичена до медіанного інтервалу,

- частота інтервалу медіанного.

Для медіани характерно, що сума відхилень від неї по модулю є мінімальною.

Мода ж є значенням ознаки, яка найбільш часто зустрічається.

Тому в залежності від того, яка особливість варіаційного ряду цікавить дослідника, повинна вибиратися одна з вищезгаданих характеристик.

3. Статистичні індекси та завдання індексного методу аналізу. Види індексів.

У статистиці під індексом розуміють специфічну відносну величину, яка характеризує зміну показника у часі та просторі.

З допомогою індексів вирішують такі завдання статистичного аналізу:

• визначають середній процент зміни показника у часі в цілому по сукупності або окремій групі;

• визначають середній процент зміни середнього значення показника;

• здійснюють порівняння показника у просторі;

• оцінюють вплив окремих факторів на зміну показника у часі або просторі.

Серед методів статистичного аналізу важливе значення займає індексний метод. Слово індекс (index) в перекладі з латини означає показник.

Індекси - це найбільш поширені статистичні показники. За допомогою індексів вивчають розвиток економіки, характеризують зміни різноманітних показників: обсягу продукції, цін, собівартості, чисельності працюючих, продуктивності праці, заробітної плати і т.д.

Індекси, перед усім - відносні показники. Разом з тим, якщо будь-який індекс - це відносна величина, то не всяка відносна величина є індексом.

Індексами називаються відносні величини, які характеризують відношення явищ у часі, у просторі, в порівнянні з плановим завданням.

Індекси можуть виражати зміну у часі і просторі як окремих одиничних простих показників (зміни обсягу виробництва чугуну, електроенергії та ін.), так і одноіменних показників по складним сукупностям (наприклад, зміна обсягу виробництва по промисловості в цілому).

Індекси, що відображають відношення простих одиничних показників, називаються індивідуальними.

Індекси, що характеризують зміну визначеного показника в цілому по будь-якій складній сукупності, називаються зведеними.

Обчислення загальних індексів, що дозволяють співвідносити між собою показники по складним сукупностям, складає особливий прийом дослідження, який називається індексним методом.

Індексний метод має свою термінологію і символіку. Для позначення індексованих величин користуються символікою:

q - кількість (обсяг) будь-якого продукту;

z - собівартість одиниці виробу;

р - ціна одиниці виробу;

t - затрати часу на одиницю виробу;

n - посівна площа;

y - врожайність окремих культур;

w - вироблення продукції за одиницю часу і т.і.

Щоб відрізнити, до якого періоду відносяться індексовані величини, біля символу знизу ставляться підстрочні знаки. Наприклад, якщо порівнюється продукція 1990 р. з продукцією 1980 р., то перша позначається через q₁, а друга - через q₀.

Виходячи з прийнятих позначень індексованих величин, легко записати для різних показників індивідуальні індекси, що позначаються через і. Так, індивідуальний індекс обсягу продукції буде виражений, як , індекс цін - , індекс собівартості - , індекс врожайності - і т.і.

В залежності від початкових даних та способу обчислення зведені індекси можуть бути агрегатними та середніми. Агрегатний індекс є основною формою індексу. Агрегатним він називається тому, що його чисельник та знаменник являють собою набір різнорідних елементів.

Найбільш типовим агрегатним індексом є індекс обсягу, або як його частіше називають, індекс фізичного обсягу.

Практично від періоду до періоду змінюються не тільки обсяг продукції, але й ціни. Тому для характеристики зміни фізичного обсягу продукції необхідно продукцію за обидва періоди розрахувати за одними й тими ж цінами, щоб усунути її вплив. При побудові агрегатного індексу фізичного обсягу в якості сумірника приймаються ціни базисного періоду (p₀).

Таким чином, формула агрегатного індексу фізичного обсягу має вигляд:

,

де - кількість продукції у звітному та базисному періодах;

р₀ - ціна базисного періоду.

абсолютний приріст складає:

Щоб визначити відносну зміну цін , обчислюють індекс цін за формулою:

Вагою у цьому індексі буде кількість виробленої продукції у звітному періоді. Цей індекс характеризує зміну цін на продукцію звітного періоду, а різниця між чисельником та знаменником відображає зміну вартості продукції внаслідок зміни цін за звітний період.

абсолютний приріст складає:

Індекс вартості продукції характеризує її зміну у звітному періоді в порівнянні з базисним за рахунок змінення q і p за формулою:

в абсолютному виразі:

Аналіз обчислених нами трьох індексів показує, що між ними існує взаємозв’язок:

Агрегатні індекси являються основною формою зведених індексів. Для їх обчислення необхідно два види показників: індексовані величини і вага. На практиці ці показники присутні не завжди. В таких випадках агрегатні індекси перетворюються в середні індекси: середній арифметичний або середній гармонійний. При цьому середній індекс має бути тотожним агрегатному індексу.

Наприклад, потрібно показати середній розмір зміни цін або собівартості визначеного набору продуктів - молока, м’яса, овочів и т.д. або середній розмір зміни заробітної плати робочих різних професій. Ці задачі можуть бути вирішені за допомогою побудови як агрегатних, так і середніх індексів.

Перетворимо агрегатний індекс фізичного обсягу в середньоарифметичний.

Формула індексу фізичного обсягу має вигляд:

Для перетворення використовуємо індивідуальний індекс індексованої величини , звідси . Замінивши у формулі агрегатного індексу фізичного обсягу продукції q₁ на i_qq₀, маємо формулу середньоарифметичного індексу фізичного обсягу:

Таким чином, вказаний індекс являє собою середню арифметичну з індивідуальних індексів, зважених по вартості продукції базисного періоду (q₀p₀).

В деяких випадках використовують середньогармонійний індекс фізичного обсягу:

середньогармонійний індекс фіз.обсягу: .

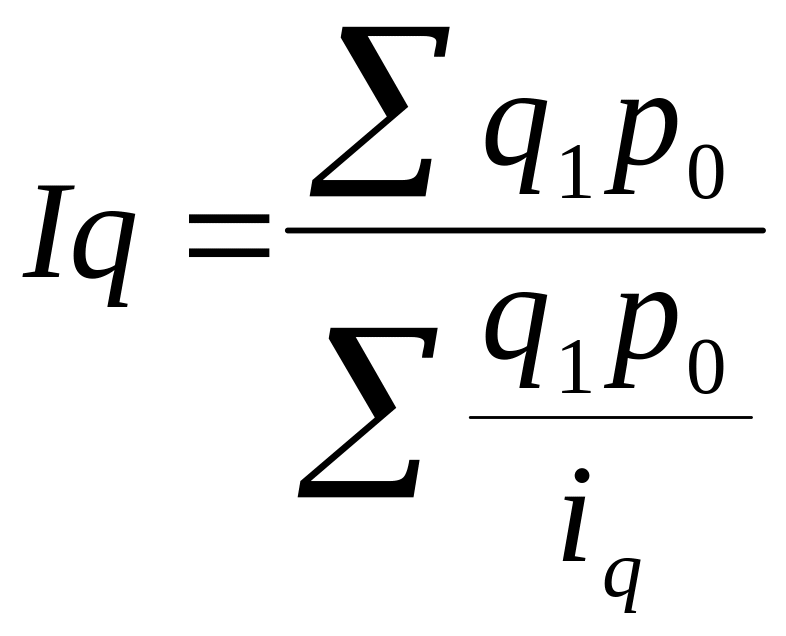В тих випадках, коли немає даних про кількість виготовленої продукції, неможливо обчислити агрегатний індекс цін. Але якщо відомі індивідуальні індекси цін, а також дані про виробництво продукції у звітному періоді в цінах звітного періоду, можна обчислити середньогармонійний індекс цін.

Для перетворення агрегатного індексу цін в середньо-гармонійний використовуємо індивідуальний індекс

, звідси .

Змінивши у формулі агрегатного індекса цін | p₀ на рівну їй величину , маємо формулу середньогармонійного індексу цін: .

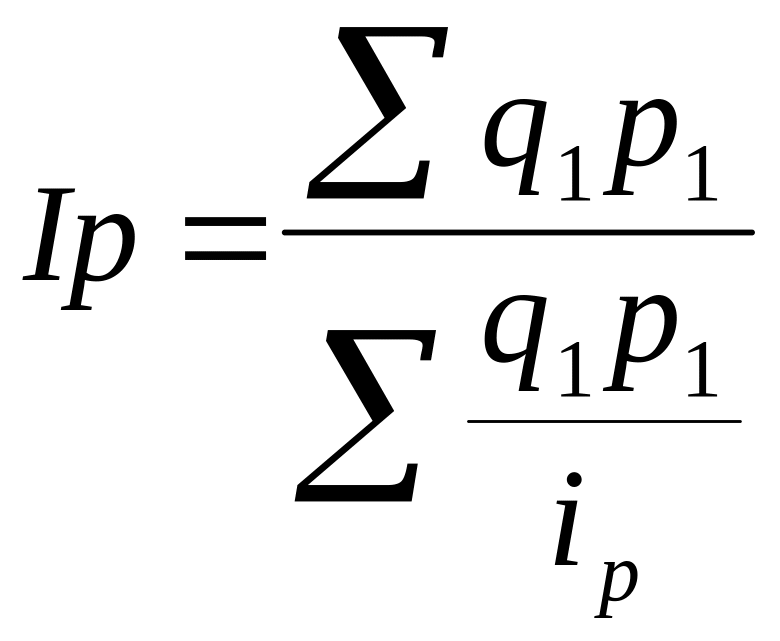Середньогармонійний індекс цін використовується в статистиці торгівлі, де в звітності вказуються дані про суму товарообігу і відсутні дані кількісного обліку проданих товарів за окремими видами (q). Тому при обчисленні індексів роздрібних цін середній гармонійний індекс знаходить широке застосування.

Індекси широко використовуються для характеристики темпів зміни суспільних явищ в динаміці. Так, наприклад, щорічно визначаються показники зміни обсягу продукції як в цілому по країні, так і в розрізі регіонів.

Якщо порівнюються показники не за два періоди, а більше, наприклад за 4 роки, то при обчисленні індексів виникає питання про вибір бази порівняння.

При визначенні темпів росту і приросту дані кожного періоду порівнюються з даними попереднього йому періоду. Але часто виникає потреба у визначенні інтенсивності зміни даних декількох періодів в порівнянні з одним будь-яким періодом, взятим за базу (початковим).

В такому випадку можуть буть обчислені базисні і ланцюгові індекси.

Базисними називаються такі індекси, при обчисленні яких, дані усіх періодів порівнюються з одним періодом, узятим за базу (початковим періодом).

Ланцюговими називаються індекси, при обчисленні яких, дані кожного періоду порівнюються з даними попереднього йому періоду. В ланцюгових індексах база - змінна.

Базисні і ланцюгові індекси можуть бути індивідуальними й загальними. Індивідуальні базисні і ланцюгові індекси - це різновид базисних і ланцюгових відносних величин динаміки. Обчислення загальних базисних і ланцюгових індексів має свої особливості.

Розрізняють загальні (базисні і ланцюгові) індекси з постійною та змінною вагою.

При обчисленні індексів з постійною вагою в якості ваги для усього ряду приймаються сумірники будь-якого одного періоду. При обчисленні індексів із змінною вагою в якості ваги кожний раз приймається сумірник другого періоду (різних років).

За допомогою індексів також аналізують динаміку середніх показників: середньої заробітної плати, середнього рівня собівартості, середньої ціни певного продукту.

В загальному вигляді динаміку таких середніх показників можна виразити у вигляді співвідношення ( ).

Зміна середньої величини того або іншого показника залежить від:

а) зміни значення кожної окремої одиниці явища, що вивчається;

б) зміни структури явища.

Наприклад, ріст середньої врожайності різноманітних видів зернових культур залежить від підвищення врожайності кожної окремої культури та від збільшення питомої ваги в загальній площі врожайних культур.

Індекс, що характеризує сумісний вплив вказаних факторів (в якому змінюються обидві ці величини), називається індексом змінного складу.

,

де - осереднена ознака;

- вага (доля) вивчаємої ознаки.

Для різноманітних якісних показників індекси змінного складу можна записати у вигляді співвідношень:

І цін змінного складу=

І собівартості змінного складу=

І врожайності змінного складу=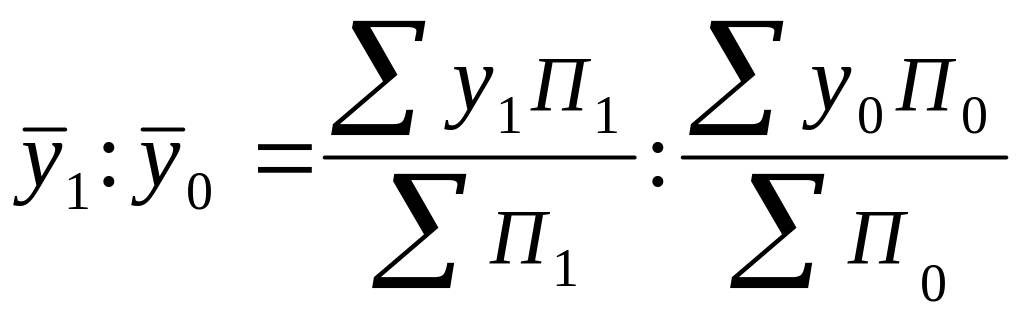 і т.д.

Таким чином, індекси змінного складу показують нам, як змінюються середні величини не тільки за рахунок зміни безпосередньо індексованого показника окремих об’єктів, але й за рахунок зміни питоми ваги цих частин в загальній сукупності (зміна складу).

Так, наприклад, середня собівартість 1т карбаміду, що випускається на різних підприємствах, залежить не тільки від рівня собівартості на окремих підприємствах, але й від кількості продукції, випускаємої різними підприємствами.

Індекс, що характеризує вплив тільки індексованої величини (змінюється тільки ця величина), називається індексом постійного складу.

І постійного складу =

Прикладами цих індексів є індекси фізичного обсягу, собівартості і т.і.

Щоб вивчити вплив зміни структури на зміни середньої величини, обчислюють індекс структурних зрушень.

І стр.зруш. =

Існує взаємозв’язок між цими індексами:

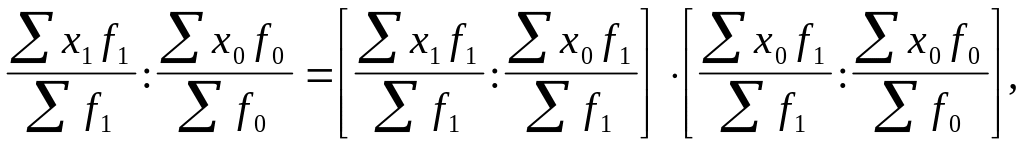
тобто І змін.сост = струк.зруш

Індексний метод дозволяє також доповнити аналіз динаміки важливих явищ абсолютними показниками.

Розрахунки, пов’язані з визначенням в абсолютному виразі зміни результативного показника за рахунок окремих факторів, називають розкладом абсолютного приросту по факторах. При даному способі розкладу абсолютного приросту ми виходимо із загального принципу побудови факторних індексів, при якому у випадку індексування якісних показників обсяговий показник фіксується на рівні звітного періоду, а якщо індексується обсяговий показник, то якісний показник фіксується на рівні базисного періоду.