11. Мінор матриці. Ранг матриці, його обчислення.

Мінором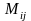 елемента 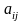квадратної матриці (1.1) називають визначник 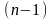-го порядку , отриманий з визначника 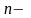го порядку 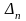викреслюванням -го рядка та 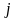-го стовпця.

Алгебраїчне доповнення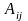 елемента визначається рівністю .

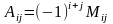Для

.

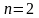
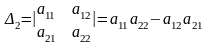Основна характеристика матриці – її ранг.

Рангом матриці називають порядок найбільшого відмінного від нуля мінора матриці.

Зручнішим у порівнянні зі звичайним перебором значень мінорів є метод знаходження рангу, який ґрунтується на тому, що ранг матриці не змінюється, якщо над матрицею виконати так звані елементарні перетворення, а саме:

1. переставити місцями два рядки (стовпці);

2. помножити кожен елемент рядка (стовпця) на один і той самий відмінний від нуля множник;

3. додати до елементів рядка (стовпця) відповідні елементи другого рядка (стовпця), помножені на одне і те саме число.

Приклад: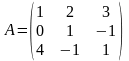 . Знайти .

Розв’язання. Зведемо матрицю до еквівалентної трикутної матриці:

~ ~

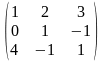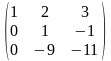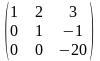
окрім мінорів 1 та 2 порядку є мінор 3 порядку 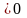. Отже .

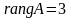12.Теорема Кронекера-Капеллі

Нехай задано систему m лінійнихрівнянь з n невідомими. Складемоосновнуматрицю А і розширенуматрицю   даноїсистеми:

 

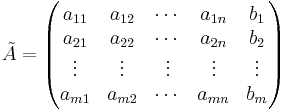
Про існуваннярозв'язкунашоїсистеми говорить теорема Кронекера-Капеллі.

Теорема (Кронекера-Капеллі) Для того, щоб система лінійнихрівняньбуласумісною, необхідно і достатньо, щоб ранг їїосновноїматрицідорівнював рангу розширеноїматриці.

Якщо ранг основноїматрицідорівнює рангу розширеноїматриці і дорівнює числу невідомих, то система маєєдинийрозв'язок.

Якщо ранг основноїматрицідорівнює рангу розширеноїматриці, але менший числа невідомих, то система маєбезлічрозв'язків.

Пояснення: =>Якщо система сумісна, то стовпчиквільнихчленів є лінійноюкомбінацієюстовпчиківосновноїматриці, а отжейогоприєднання до системи не збільшить рангу сукупностістовпчиківосновноїматриці. <= навпаки, якщоприєднаннястовпчикавільнихчленів до сукупностістовпчиківосновноїматриці не збільшує рангу систвекторів, то цеозначає,щоцейстовпчиквільнихчленів є лінійноюкомбінацієюстовпчиківосновноїматриці, а отже система є сумісною.

15.Лінійно не залежні вектори (лінійнанезалежністьмножинивекторів) — множинавекторів, які не утворюютьнетривіальнихлінійнихкомбінаційрівних нулю.

Якщо   векторнийпростір над полем   і множинавекторів  .

•  називаєтьсялінійнонезалежною, якщо будь-яка йогоскінченна підмножина є лінійнонезалежною.

• Скінченнамножина   називається лінійнонезалежною, якщо лінійнакомбінація векторівдорівнює нулю тільки в тривіальномувипадку, тобто:

Приклад 1. Визначити лінійну залежність або незалежність системи векторів  = (-1,-2,-3);  = (7,8,9);  = (-4,-5,6) та системи векторів  = (3,-2,4,1); = (-1,2,-1,2);  = (1,2,2,5).

Розв’язування. Спочатку розглянемо систему векторів  ,   та  . Знайдемо ранг матриці, складеної з координат цих векторів:

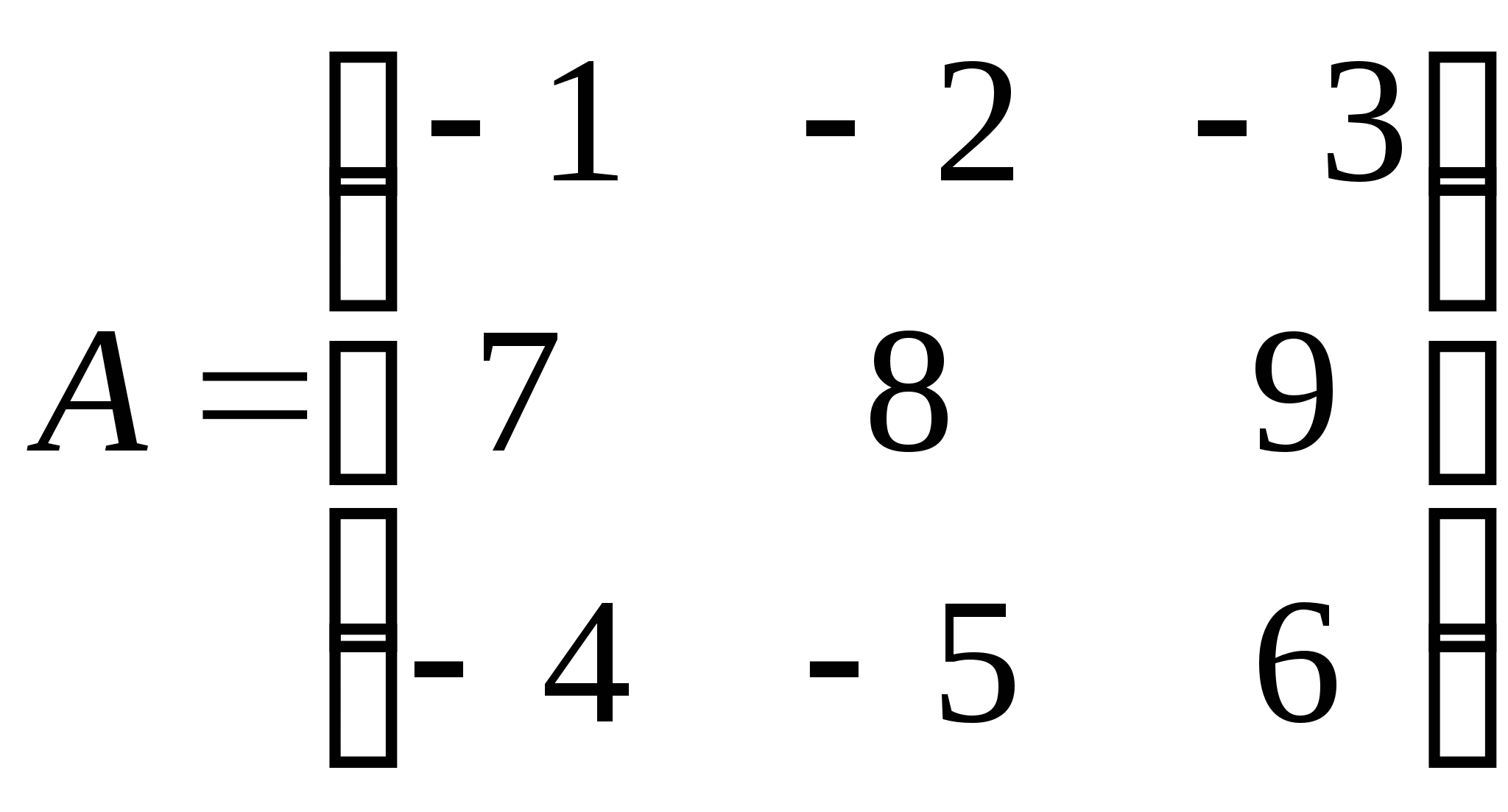
Визначник цієї матриці |А| = - 48 + 72 + 105 – 96 +84 – 45 = 72 не дорівнює нулю, тому r(A)=3 і вектори  ,  ,  лінійно незалежні.

Тепер розглянемо систему векторів  ,  ,  . Матриця В складена з координат цих векторів має вигляд:

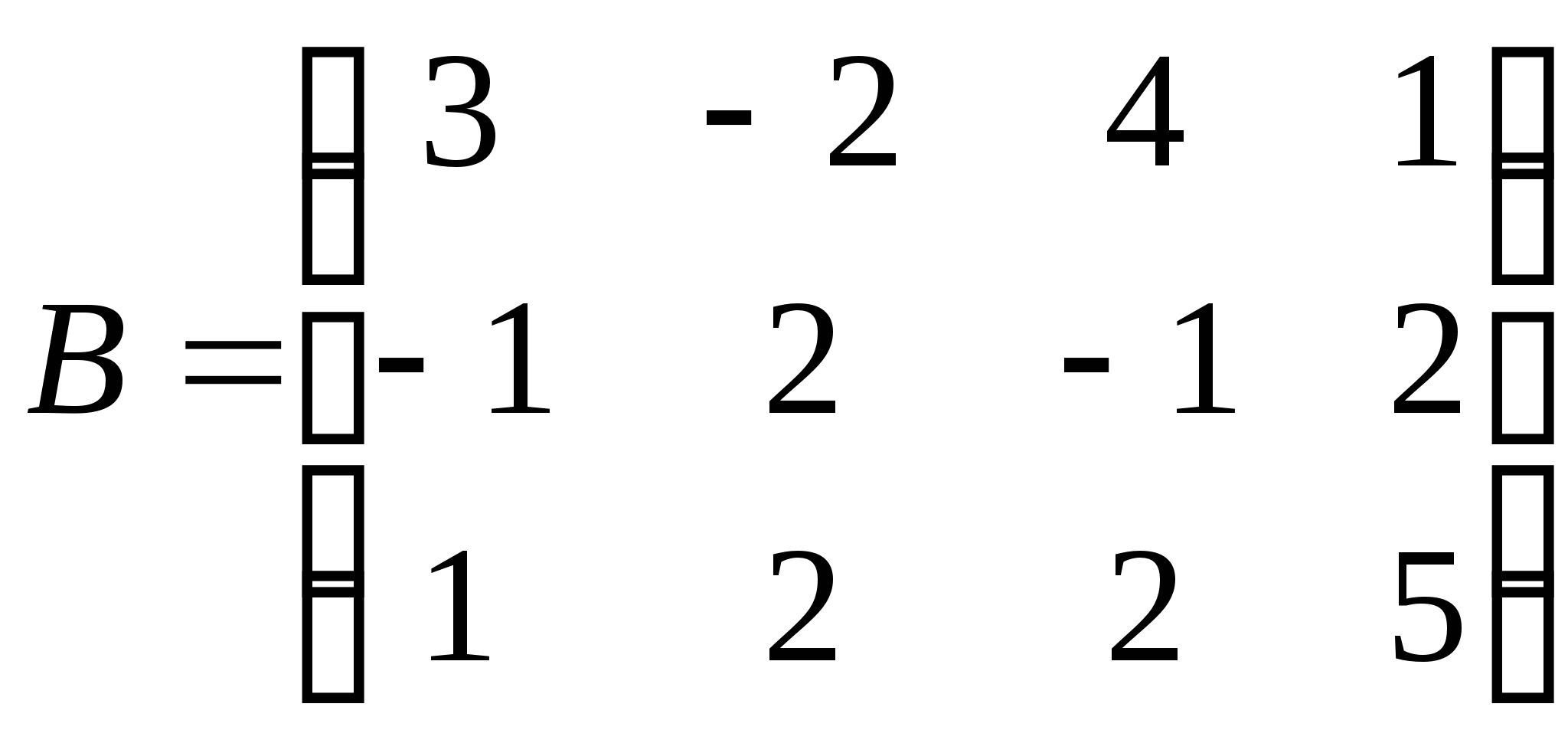
Ця матриця розміру 3 х 4 має ранг r(B)=2.

Тому вектори  ,  ,   лінійно залежні.

Базисом векторного простору L називаєтьсявпорядкованийнабірвекторів {e1, …, en} , якщокожний вектор із L можна однозначно представити у вигляділінійноїкомбінації

Або, просто кажучи,базис - цеодиничнівектори, відкладені на системі координат