Лабораторные работы №1-3 / ЛАБА №2

Лабораторная работа № 2

Управление запасами.

Цель работы: Исследование методов управления запасами с целью минимизации общих затрат.

Порядок выполнения работы:

1. Сформулировать общую задачу управления запасами. Дать определения затратам.

2. Описать основную модель. Вывести формулу оптимального запаса. Привести график стоимости затрат. Решить задачу.

3. Описать модель производимых поставок, определить общие издержки и оптимальный размер поставок. Привести график функции изменения запаса и стоимости затрат.

4. Описать модель поставок со скидкой, пояснить разрывность функции стоимости затрат. Решить задачу.

Задача управления запасами состоит в том, чтобы избежать общих крайностей и сделать общие затраты как можно меньше. Рассмотрим три модели управления запасами:

1.Основная модель управления запасами.

Важная роль в задачи будет играть функция изменения запаса, это связь между количеством единиц товара на складе Q и временем t.

Будем считать, что имеется один вид товара.

Если на товар имеется спрос, то функция изменения запаса Q = Q(t) уменьшается. Ели товар завозят на склад, то Q = Q(t) увеличивается.

Будем считать возможным мгновенное выполнение запаса. Затраты связанные с запасами можно разделить на три части:

1. Стоимость товара.

2. Организационные издержки.

3. Издержки на хранение.

Рассмотрим основные величины, принятые в рамках основной модели. Будем использовать в качестве единиц условные единицы (у.е).

В качестве измерения времени 1-н год.

c – цена одной единицы товара.

d – интенсивность спроса.

s – организационные издержки.

h – издержки на хранение.

q – постоянный размер одной партии товара.

Параметры: c,d,s,h – считаются заданными.

Задача управления запасами состоит в том выборе параметра q, таким образом, чтобы минимизировать годовые затраты.

Поскольку годовая интенсивность спроса равна d, а цена единицы товара равна c, то общая стоимость товара в год равна c*d (у.е).

Поскольку в одной партии q единиц товара, а годовой спрос равен d, то число поставок равно d/q.

И организационные издержки равны .

Средний уровень запаса равен .

Поскольку годовые издержки на хранение равны h, то общие издержки на хранение товара равны .

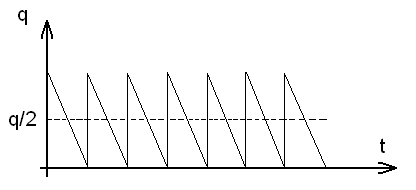
Таким образом, общие издержки:

C = cd + ds/q + qh/2

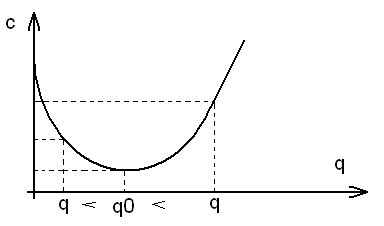
Оптимальное q^o = .

Полученная формула называется формулой оптимального запаса или формулой Харриса.

2. Модель производственных поставок.

Если товары поставляются с работающей производственной линией, то необходимо модифицировать к параметрам с,s,d,h добавляется еще производительность производственной линии p (ед. тов. в год).

Эта новая модель называется моделью производственных поставок.

Величина q – размер партии.

График функции изменения запаса имеет вид:

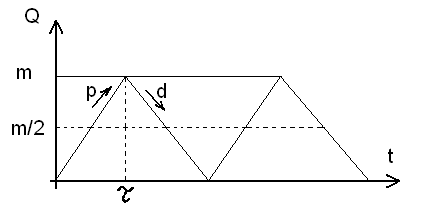
 - время поставки.

C(q) как и в основной модели состоят из трех частей.

Годовые издержки .

Издержки на хранение .

Общая стоимость cd.

 - время поставки, в течении этого времени происходит как накопление с интенсивностью p, так и расходование с интенсивностью d.

p-d – скорость

pd.

Максимальный уровень запаса вычисляется по формуле:

M = (p-d)

Заметим, что M<q; p=q отсюда следует

M = (p-d)q/d.

Средний уровень запаса M/2 таким образом издержки на хранение запаса равны отсюда следует, что основные издержки равны:

.

Оптимальный размер поставок:

.

Отсюда следует:

3. Модель поставок со скидкой.

Рассмотрим ситуацию, описываемую в целом основную модель, но с одной особенностью, которая состоит в том, что товар можно поставлять по льготной цене со скидкой, если размер партии достаточно велик, иными словами, если товар поставляется по цене c₀<c.

Функция издержек c_q задается в таком случае следующим образом:

если q<q₀

если q>q₀

Нетрудно заметить, что функция C_q в точке q = q₀ разрывна.

.

.

Для выяснения вопроса о том какой размер партии оптимален следует сравнить значение функции C(q) в точке q и q₀.

И та точка где функция C(q) примет меньшее значение, будет оптимальным размером партии q₀ в модели поставок со скидкой.

Может случиться, что C(q) = C(q₀).

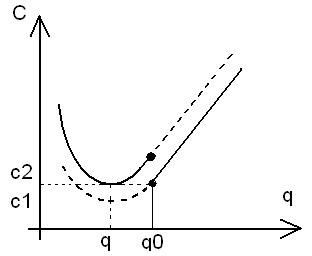
с1=с2

Можно взять любое из чисел.

Задача № 1.

Интенсивность спроса составляет 6 тыс. ед. товара в год. Издержки на организационные поставки составляют 13 у.е. за партию. Стоимость равна 7 у.е. издержки на хранение 1,5 у.е. в год. Найти q оптимальное, продолжительность цикла, число поставок за год, нарисовать график Q(t).

Дано :

d=6 тыс. ед. товара в год

s=13 у.е.

c=7 у.е.

h=1.5 у.е.

Решение:

=

.

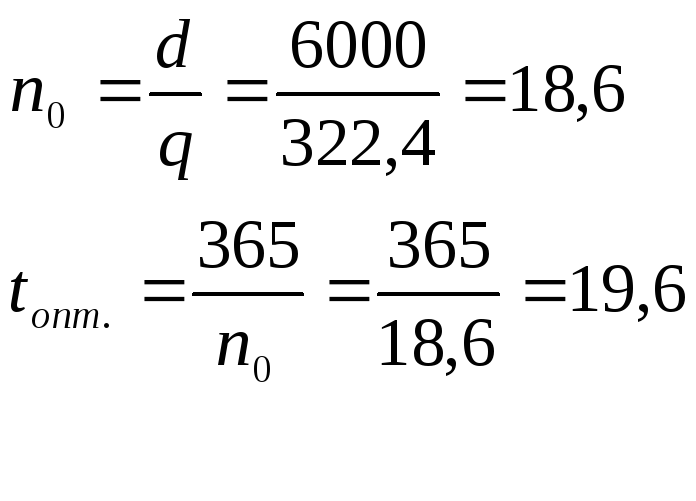Строим график зависимости Q(t).

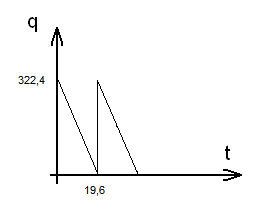
Строим график зависимости C(q).

C

q

Задача № 2.

Интенсивность равномерного спроса составляет 6000 тыс. тов. в год. Товар поставляется с конвейера производительностью 30000 ед. тов. в год. Организационные издержки равны 13 у.е. Издержки на хранение товара

1,5 у.е. Цена за товар равна 7 у.е.

Определить оптимальный размер партии q_оптим., продолжительность поставки , продолжительность Т, М/2 средний уровень запасов. Построить графики.

Дано:

d = 6000 тыс.

P = 30000 ед.

s =13 у.е.

h =1,5 у.е.

с = 7 у.е.

Найти :

q_оптим=?,=?,T=?,=?

Решение:

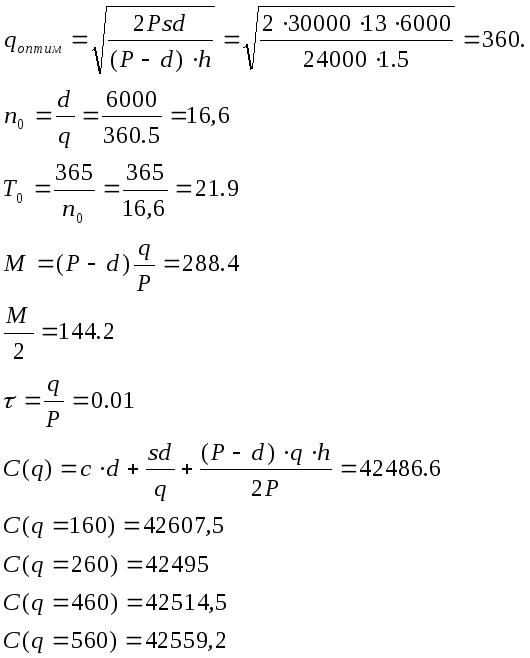
C

q

Задача № 3.

Торговец имеет обильность спроса на товар 6000 ед. в год. Товар он покупает у поставщика за 7 у. е. Издержки на хранение 1,5 у. е. Если торговец покупает сразу партию 150 ед. товара или более, то цена 5 у. е. за 1 шт. Каков оптимальный размер партии, если годовые затраты на хранение товара 3 у. е.

Нарисовать график C(q) и определить точку разрыва.

Дано:

d = 6000 у.е.

с = 7 у. е.

s=13 у.е.

h=1, 5 у.е.

c1=7 у.е.

c2=5 у.е.

Решение:

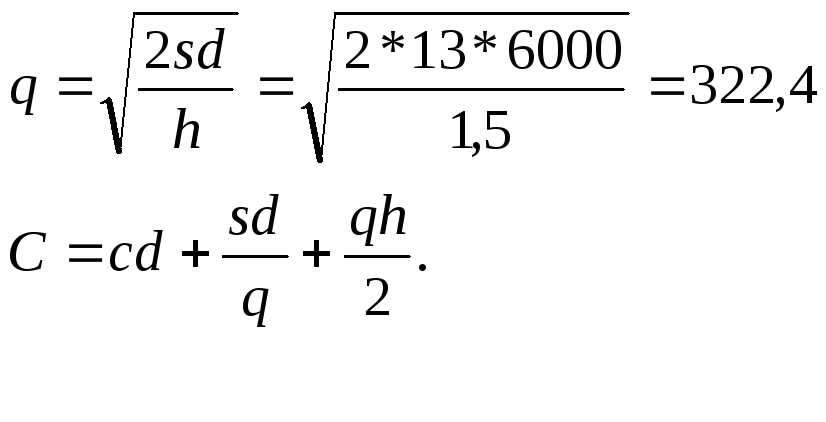
Зависимость С(q) при с=5 у. е.

Зависимость С(q) при с=7 у.е.

Строим график C(q).

C

q