4. Модулятор.

В модуляторе синхронная двоичная случайная последовательность биполярных импульсов b(t) осуществляет модуляцию гармонического переносчикаe(t)=U_m cos(2πft),U_m=1В,f= 100V’_n)

Для частотной модуляции (ЧМ):

«0» − U₀(t) = U_m cos(2π(f-f)t);

«1» − U₁(t) = U_m cos(2π(f+f)t).

Требуется:

1. Записать аналитическое выражение для модулированного сигнала.

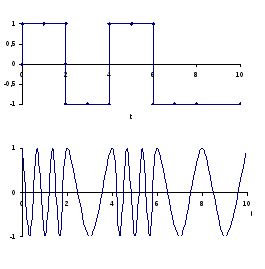
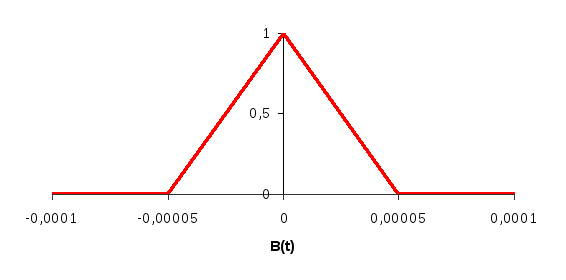
2. Изобразить временные диаграммы модулирующего b(t) и модулированногоu(t) =u(b(t)) сигналов, соответствующие передачtj-го уровня сообщенияa(t).

3. Привести выражение и начертить график корреляционной функции модулирующего сигнала В(τ).

4. Привести выражение и начертить график спектральной плотности мощности модулирующего сигнала G_В(ω).

5. Определить ширину энергетического спектра модулирующего сигнала ∆F_B из условия ∆F_B=αV_k(где α выбирается в пределах от 1 до 3). Отложить полученное значение ∆F_Bна графике G_В(f).

6. Привести выражение и построить график энергетического спектра G_u(ω) модулированного сигнала.

7. Определить ширину энергетического спектра ∆F_uмодулированного сигнала и отложить значение ∆F_uна графике G_u(f).

Решение:

1) f₀ = 100·V’_n =2·10⁶Гц;f==1/5·10^-5=20000;

При частотной модуляции:

U₀(t) = cos U_m cos(2π(f-f)t)=cos(12434400t);

U₁(t) = cos (2π(f+f)t).=cos(12685600t).

3)

,

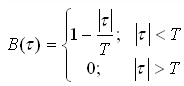где Т =5·10^-5 с

4)

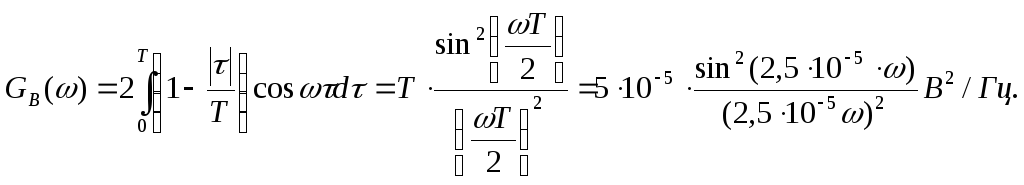
График спектральной плотностимощности модулирующего сигнала G_В(f):

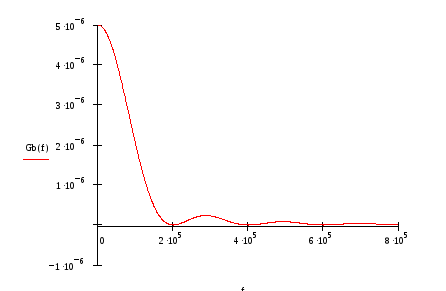
5)

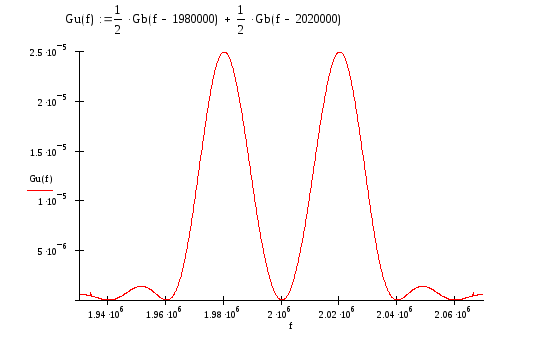
6) G_u(f) = G_B(f—f₀), где f₀ = V’_n∙100 = 2∙10⁵ Гц. (То есть график функции G_u(f) смещается на значение f₀ вправо относительно оси ординат.)

7)

5. Канал связи

Передача сигнала U(t) осуществляется по каналу с постоянными параметрами и аддитивным флуктуационным шумомn(t) с равномерным энергетическим спектромN₀/2 (белый шум).

Сигнал на выходе такого канала можно записать следующем образом:

z(t) =U(t) +n(t)

Требуется:

1. Определить мощность шума в полосе частот F_k= ∆F_u ;

2. Найти отношение сигнал – шум Р_с /Р_ш;

3. Найти пропускную способность канала С;

4. Определить эффективность использования пропускной способности канала К_с, определив ее как отношение производительности источника Н^’к пропускной способности канала С.

Решение:

1) В².

2)

Тогда .

3) С = ∆F_U·log₂(1+P_c/P_Ш) = 1,24·10⁵ бит/с.

4) К_с = Н^’/С = 0,2848.

6. Демодулятор

В демодуляторе осуществляется оптимальная когерентная или некогерентная (в зависимости от варианта) обработка принимаемого сигнала z(t) =U(t) +n(t).

Требуется:

1. Записать алгоритм оптимального приема по критерию минимума средней вероятности ошибки при равновероятных символах в детерминированном канале с белым гауссовским шумом.

2. Нарисовать структурную схему оптимального демодулятора для заданного вида модуляции и способа приема.

3. Вычислить вероятность ошибки ρ оптимального демодулятора.

4. Определить, как нужно изменить энергию сигнала, чтобы при других видах модуляции и заданном способе приема обеспечить найденное значение вероятности ошибки ρ.

Решение:

1)

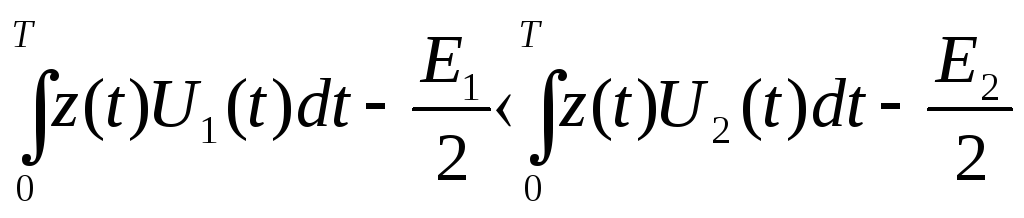
2)

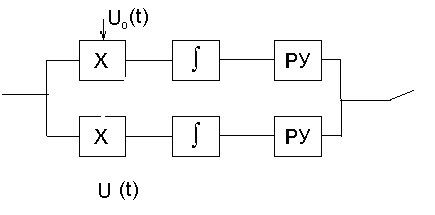
3) ρ= 1/2 (1-Ф(х));

Ф(х) – функция Крампа

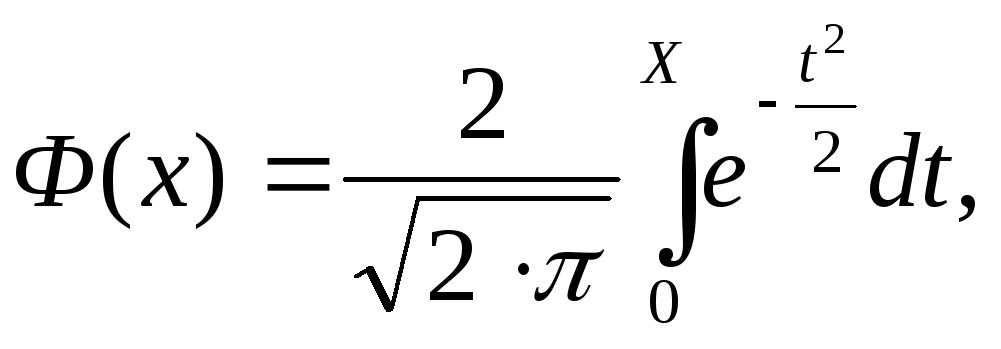где.

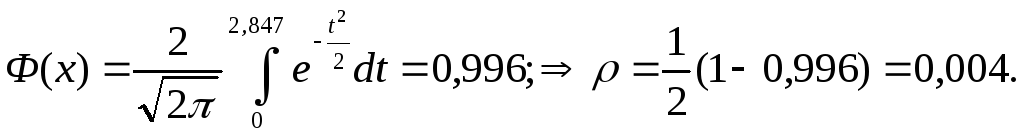
4. При частотной модуляции энергетический выигрыш по пиковой мощности составляет в два раза по сравнению с АМ и проигрывает два раза по сравнению с ФМ.

По средней мощности: проигрывает два раза по сравнению к ФМ и равен по сравнению АМ.