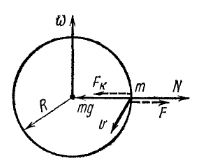
Тема 5 неінерціальні системи відліку

5.1 Основні поняття і співвідношення

Другий закон Ньютона в неінерціальних системах відліку має вигляд:

,

де - сума всіх сил, що діють на дане тіло з боку інших тіл, - сила інерції, - прискорення тіла в неінерціальній системі відліку.

В системах відліку, що рухаються поступально , де - прискорення, з яким рухається неінерціальна система відліку.

В системах відліку, що обертаються діють :

Відцентрова сила інерції: , та сила Коріоліса .

5.2. Методичні вказівки до розв’язування задач

В задачах, в яких розглядаються фізичні процеси, що відбуваються всередині тіла, що рухається прискорено (вагоні, ліфті і таке інше), розв’язок, який ґрунтується на застосуванні другого закону Ньютона, спрощується, якщо розглядати явище в неінерційній системі відліку, зв’язаної з тілом, що рухається прискорено. Відповідно двом рухам тіла – поступальному і обертальному – застосовують неінерціальні системи відліку, що рухаються поступально і обертально. В неінерціальних системах відліку, що рухаються поступально, другий закон Ньютона виражається рівнянням (1) , де - сума всіх сил, що діють на дане тіло з боку інших тіл, - сила інерції, - прискорення тіла в неінерціальній системі відліку. Це ж рівняння можна застосовувати і в системах відліку, що обертаються при умові, що матеріальна точка (частинка) в цій системі знаходиться в стані спокою. Тоді у виразі (1) , - доцентрове прискорення тієї точки системи відліку, що обертається, в якій знаходиться дана частинка. Величину називають відцентровою силою інерції.

Сила інерції, що входить у рівняння (1) існує тільки в неінерціальній системі відліку і для неї не можна вказати тих конкретних тіл, з боку яких вона діє.

5.3 Приклади розв’язування задач.

1. Неінерціальні системи координат, що рухаються прямолінійно

Розв’язок: Застосовуються рівняння руху.

2. Неінерціальна система координат, що рухається зі сталою кутовою швидкістю.

Розв’язок: Застосовуються рівняння руху.

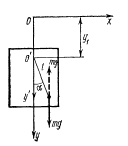
Перший тип задач.

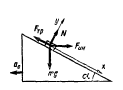
Рис. 5.1

Приклад 5.1. Тіло масою , що знаходиться на вершині похилої площини, утримується силою тертя. За який час тіло спуститься по похилій площині, якщо вона стане рухатись в горизонтальному напрямі з прискоренням =1,00м/с². Довжина площини =1,00м, кут нахилу до горизонту =300, коефіцієнт тертя між тілом і площиною =0,60.

Розв’язок. Виберемо систему відліку, пов’язану з похилою площиною. Поки площина перебуває в стані спокою, на тіло діють три сили: сила тяжіння , сила нормального тиску опори і сила тертя спокою , які зрівноважують одна одну. Як тільки починається прискорений рух площини і «прив’язана» до неї система відліку стане неінерціальною, з’явиться четверта сила, що діє не тіло, - сила інерції . Рівновага порушиться і тіло почне ковзати вниз по похилій площині з прискоренням . Оскільки шуканий час визначається відомою формулою шляху рівноприскореного руху без початкової швидкості:

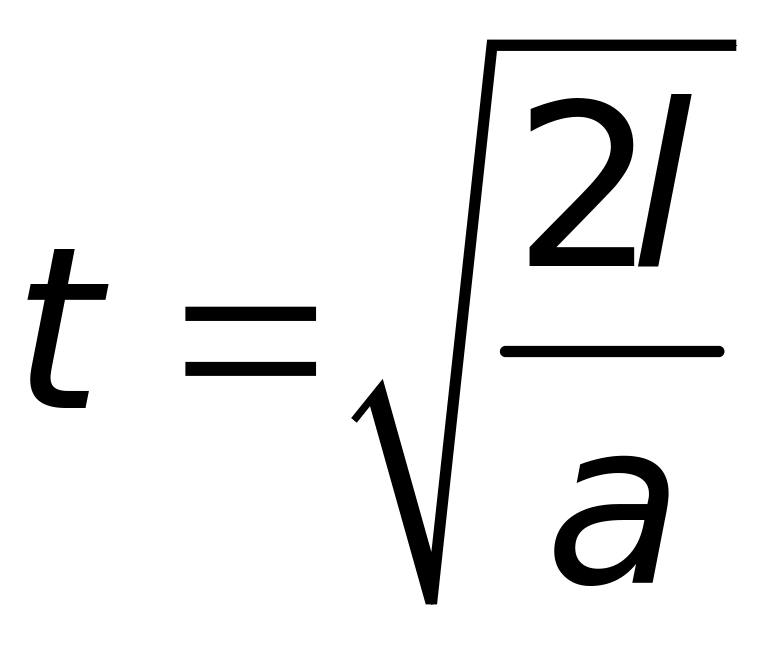, (1)

то необхідно знайти прискорення . Для цього запишемо другий закон Ньютона в неінерціальній системі відліку:

. (2)

Виберемо осі проекцій, як показано на рисунку. Проектуючи всі вектори, що входять в рівняння (2), на осі і , одержимо відповідно два скалярних рівняння:

(3)

(4)

Розв’язавши системі (3),(4) з урахуванням , знайдемо прискорення.

Тепер за формулою (1) маємо:

.

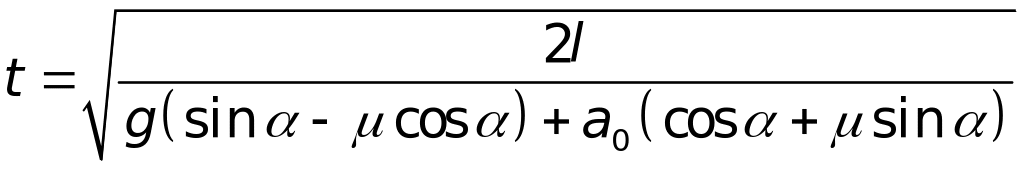Підставивши числові значення величин, знайдемо:

Приклад 5.2. Посудина з рідиною обертається навколо вертикальної осі зі сталою кутовою швидкістю . Визначити форму поверхні рідини.

Розв’язок. Кожна точка посудини з рідиною, що обертається має прискорення, що напрямлене до осі обертання, яке рівне , де - відстань точки від осі обертання. Розглянемо явище в неінерціальній системі відліку, прив’язаної до посудини, що обертається. В ній рідина буде нерухомою. Розв’яжемо задачу двома способами, що відповідають двом методам пояснення поведінки тіла в неінерціальній системі відліку:

Рис. 5.2 а

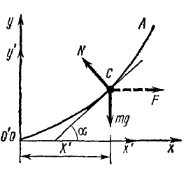
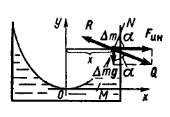
1 спосіб. На частинку рідини масою , що знаходиться на поверхні на відстані від осі обертання, діють три сили, рис. 5.2 а

1) сила тяжіння ;

2) відцентрова сила інерції ; сила реакції сусідніх частинок рідини.

Рівнодійна зовнішніх сил, що діють на частинку рідини в стані спокою, повинна бути напрямлена по нормалі до поверхні рідини в даній точці (тут зовнішніми є сили і , а сила - їх рівнодійна). Інакше існувала б напрямлена по дотичній складова сили , яка викликала б ковзання частинки по поверхні рідини.

Звідси можна знайти кут нахилу дотичної до лінії горизонту (осі ). Як видно з рисунка:

.

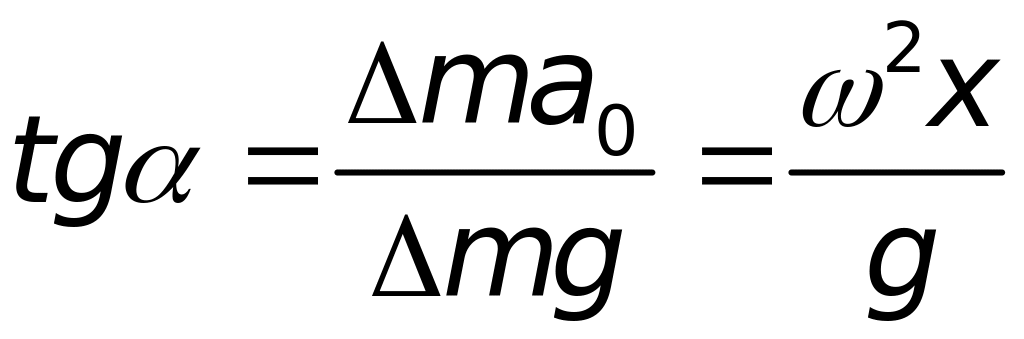Враховуючи, що 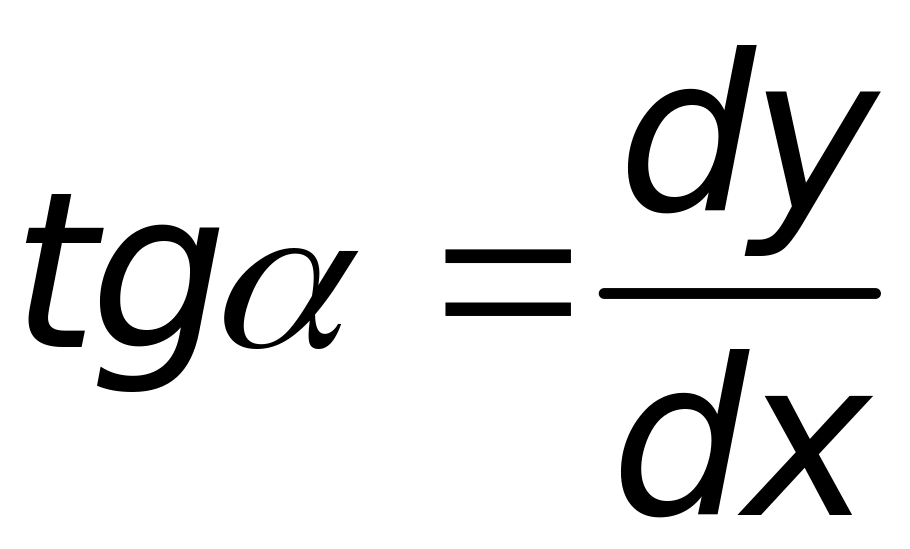, отримаємо диференціальне рівняння кривої, обертання якої навколо осі утворює поверхню рідини:

,

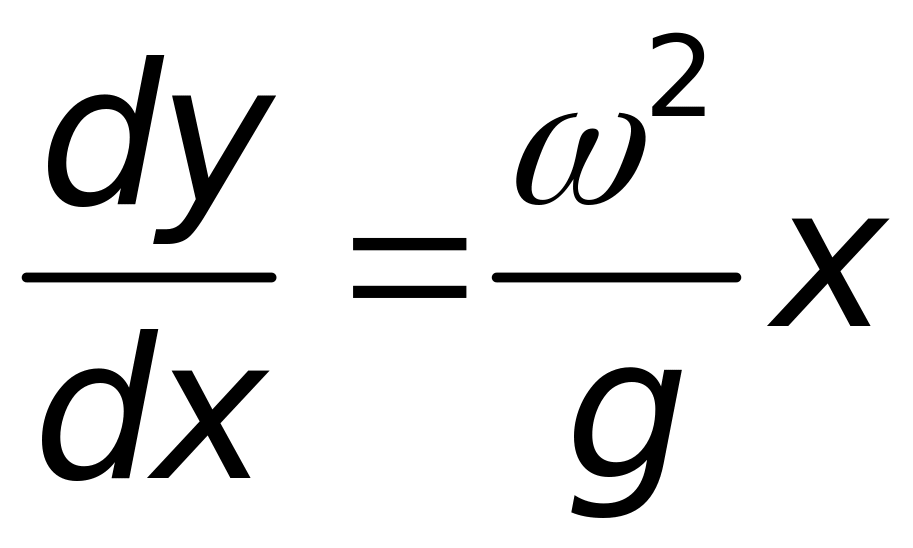Звідки

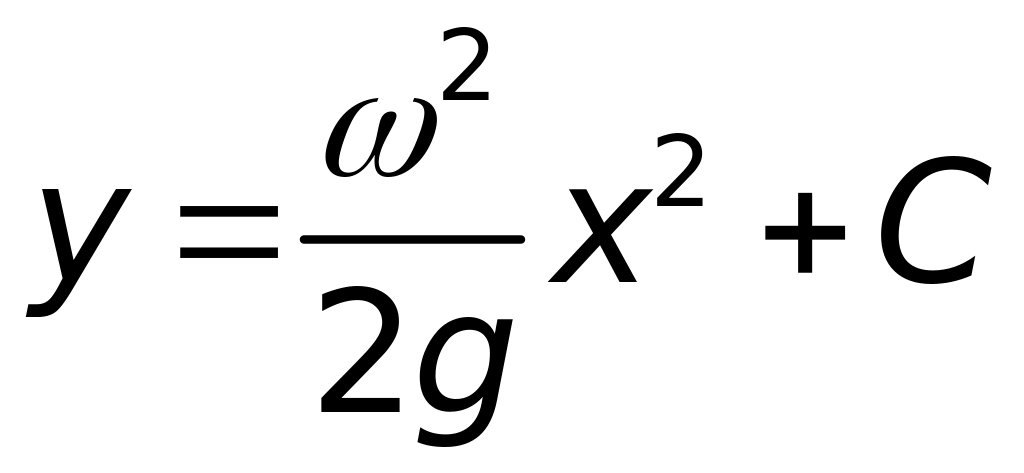(1)

Очевидно, при заданому виборі осі стала =0

З формули (1) випливає, що крива – парабола. Отже, поверхня рідини є параболоїдом обертання.

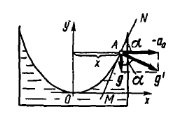
Рис. 5.2 б

2 спосіб. Не будемо вводити сили інерції, але врахуємо, що при обертанні посудини в зв’язаній з нею системі відліку змінюється поле тяжіння. При цьому нове прискорення сили тяжіння виражається через старе прискорення співвідношенням .

Виберемо точку поверхні рідини, рис. 5.2 б, розташовану на відстані від осі обертання. Нехай вектори і утворюють в цій точці кут . Оскільки поверхня рідини в стані спокою завжди нормальна до напрямку сили тяжіння, то, як видно з рисунка, між дотичною і лінією горизонту (віссю ) також буде кут , при цьому

.

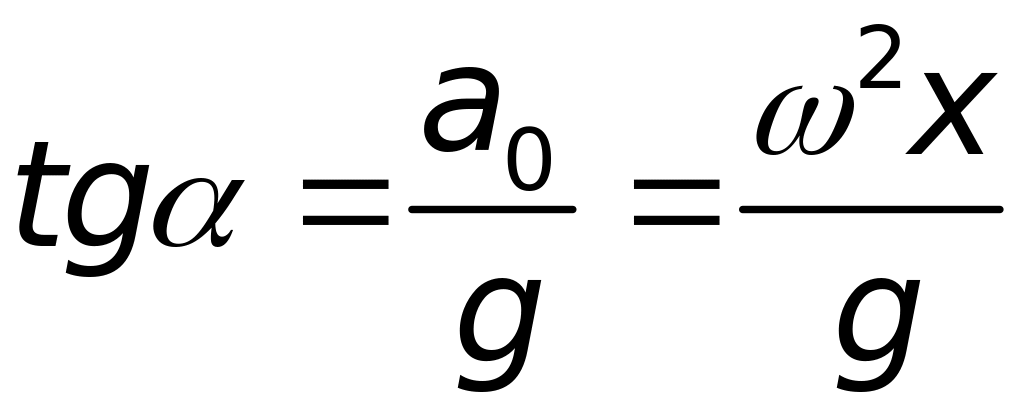Подальший хід розв’язку співпадає з тим, що отримано в першому способі.

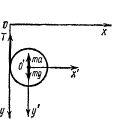
Рис. 5.3

Приклад 5.3. Однорідний круглий циліндр з намотаними на ньому двома тонкими нитками із закріпленими верхніми кінцями опускається вниз і обертається навколо своєї осі симетрії, рис. 5.3. Не враховуючи сил тертя, визначити прискорення точок, що лежать на осі циліндра.

Розв’язок. В неінерціальній системі координат до сил взаємодії і необхідно додати силу інерції - . Для рівнянь руху в цьому випадку маємо:

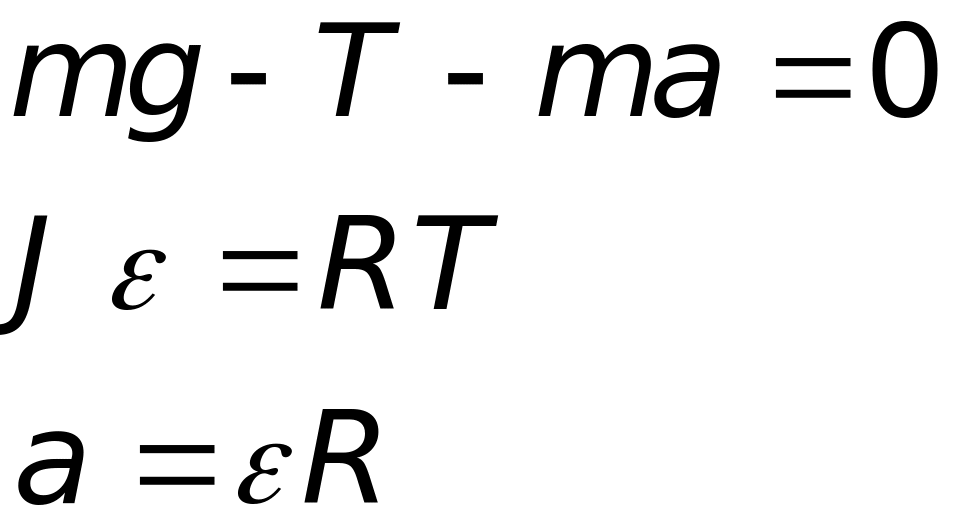
де - вага циліндра, - натяг двох ниток, - момент інерції циліндра відносно його осі, - кутове прискорення, - радіус циліндра. При ці рівняння дають:

.

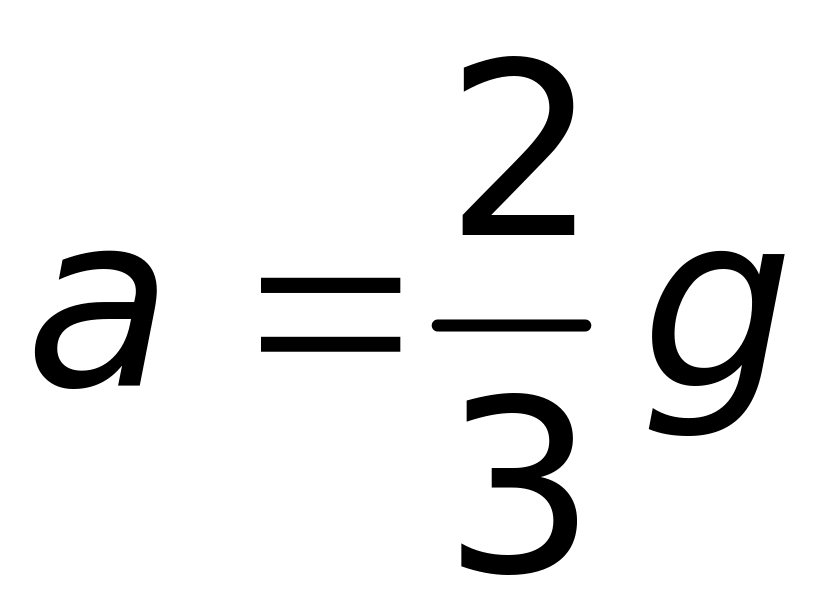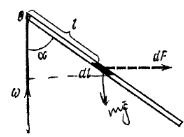
Рис. 5.4

Приклад 5.4. Однорідний стержень підвішений на нитці і спирається кінцем на абсолютно гладку площину, рис. 5.4. Точка підвісу починає рухатися горизонтально з прискоренням , при якому вісь стержня і нитка утворюють пряму лінію з кутом до горизонту. Визначити це прискорення і величину реакції при русі.

Розв’язок. В неінерціальній системі відліку до звичайних сил взаємодії (натяг нитки , сила тяжіння і ) необхідно додати силу інерції - .

Сума моментів сил відносно точки дає:

,

де - половина довжини стержня.

Для величини шуканого прискорення одержимо:

Рівняння моментів відносно центра мас стержня дає:

,

де - момент інерції стержня відносно точки центра мас, - кутове прискорення обертання стержня. Оскільки =0, то при , одержимо, що =0.

Для визначення прискорення можна скористатися рівняннями:

,

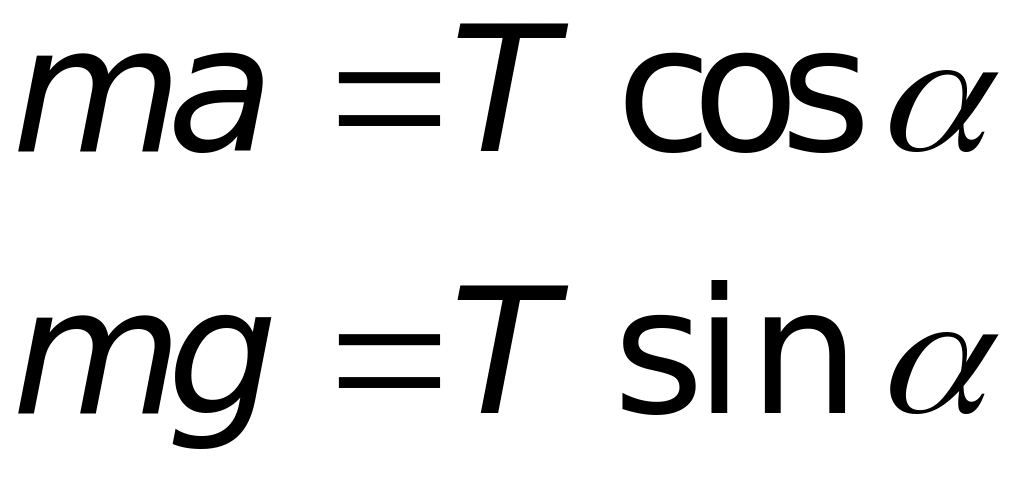де - маса стержня, - прискорення вільного падіння. Ці рівняння дають:

.

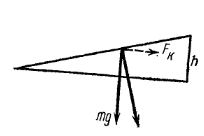
Рис. 5.5

Приклад 5.5. Математичний маятник з довжиною нитки і масою кульки підвішений на дошці, що вільно падає (з прискоренням ). Як буде рухатись маятник (кулька) відносно дошки, якщо вона починає свій рух в момент, коли швидкість кульки не дорівнює нулю?

Розв’язок. В неінерціальній системі координат крім сили тяжіння і натягу нитки необхідно врахувати силу інерції - . Сума моментів всіх трьох сил відносно точки дорівнює нулю. Для рівняння обертового руху маятника це дає:

,

де - момент інерції маятника, - кут відхилення маятника, - його кутове прискорення. З цього рівняння випливає, що =0. Маятник буде обертатися зі сталою кутовою швидкістю:

.

В інерціальній системі для координат маятника

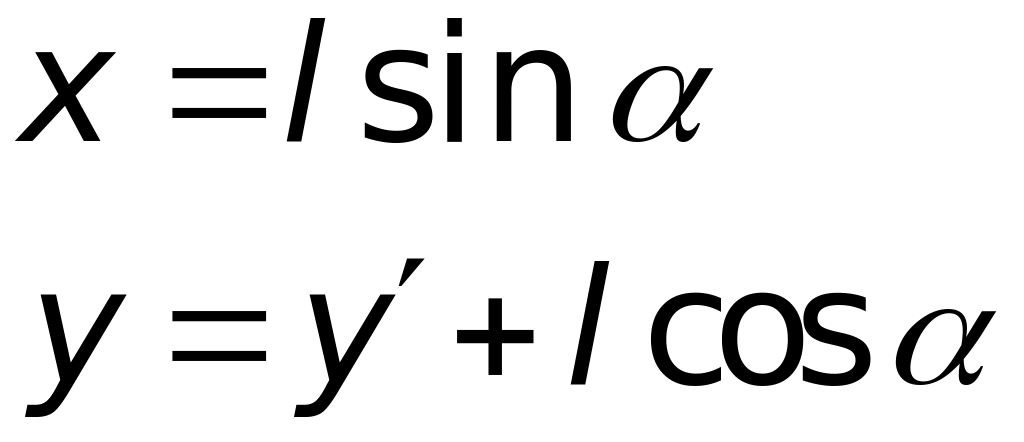
Для рівнянь руху

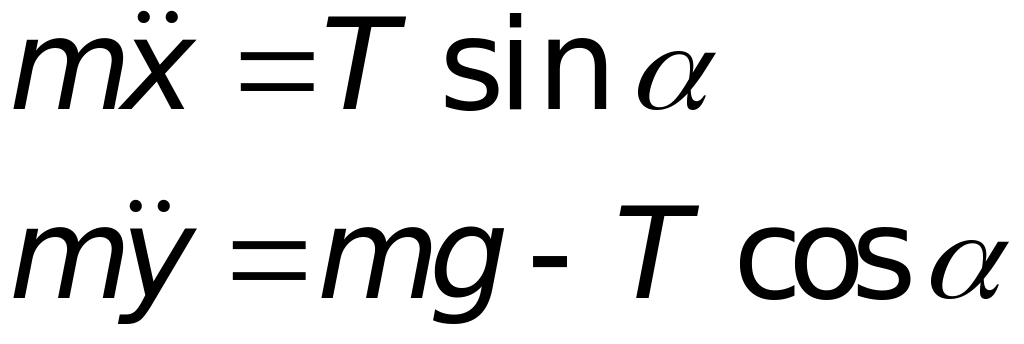
Для компонентів прискорення отримаємо:

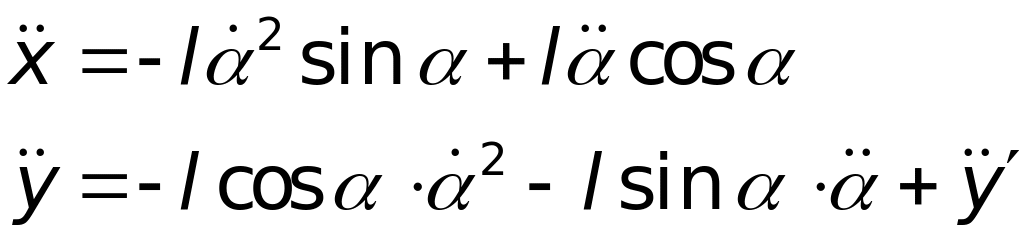
Вважаючи, що , , , з рівнянь руху отримаємо:

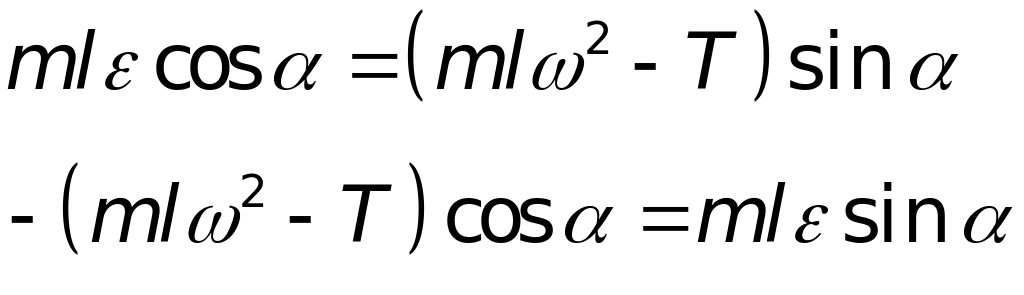
Ці два рівняння сумісні, якщо:

і .

Перше рівняння дає величину сили , прикладеної до кульки. Друге призводить до сталої кутової швидкості обертання маятника:

.

Другий тип задач.

Приклад 5.6. Вигнутий стержень ОА, рис. 5.6, може обертатися навколо вертикальної осі . На стержні є кільце С, яке може вільно, без тертя переміщуватися по стержню. Визначити рівняння (форму) стержня, при якому кільце при будь-якій кутовій швидкості обертання стержня не буде по ньому переміщатися.

Рис. 5.6

Розв’язок. 1. В неінерціальній системі координат , що обертається зі сталою кутовою швидкістю , до сили тяжіння і реакції опори слід додати відцентрову силу інерції , де - маса кільця, - відстань кільця від осі обертання (вісь ).

Щоб кільце перебувало в стані спокою при будь-якій кутовій швидкості обертання стержня, необхідно, щоб сума всіх сил вздовж напрямку можливого переміщення була рівна нулю, тобто:

,

де - прискорення сили тяжіння, - кут між дотичною до лінії стержня в точці, де знаходиться кільце, і віссю . З цього рівняння отримуємо:

.

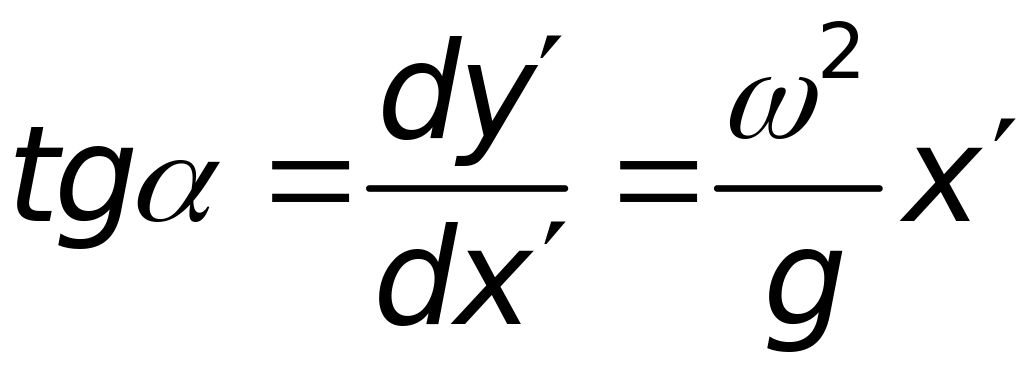Інтегрування дає рівняння параболи:

.

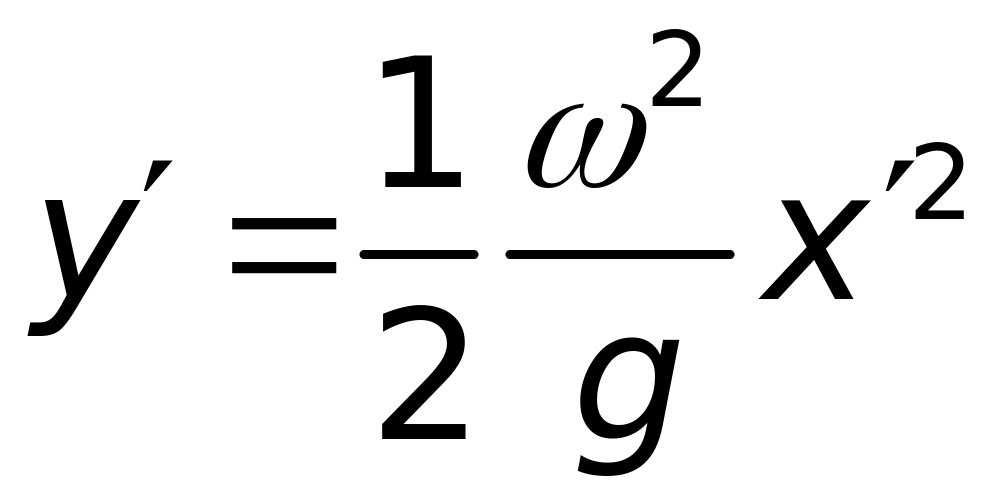2. В інерціальній системі координат доцентровою силою буде векторна сума сил тяжіння і реакція опори кільця. Маємо:

.

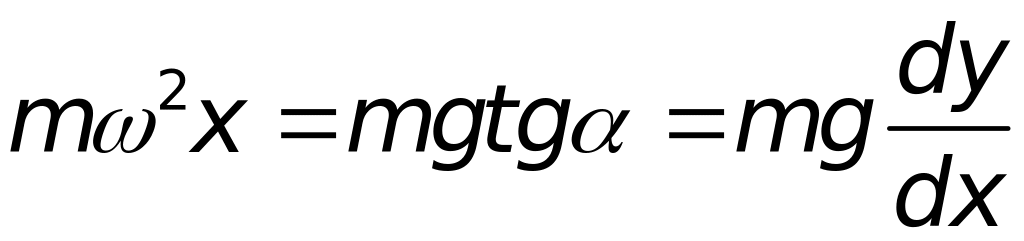Інтегрування дає, як і в попередньому випадку, рівняння параболи:

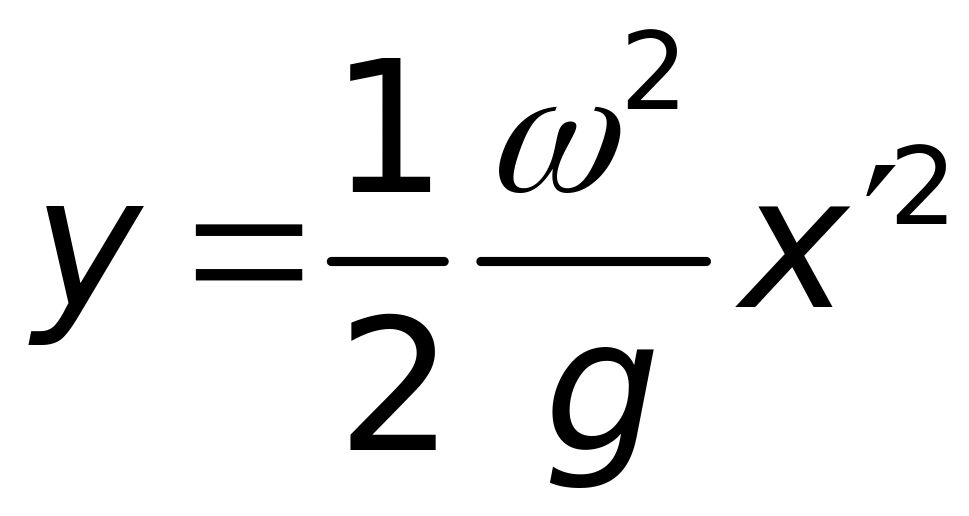
Рис. 5.7

Приклад 5.7. Тонкий однорідний стержень довжиною , рис. 5.7, і масою обертається за інерцією зі сталою кутовою швидкістю навколо вертикальної осі, що проходить через його верхній кінець О. Визначити кут стійкого обертання стержня.

Розв’язок. В неінерціальній системі координат, що обертається разом зі стержнем, до кожного елементу довжини стержня буде прикладена елементарна відцентрова сила інерції

,

де - площа поперечного перерізу стержня, - його густина, - відстань елемента стержня від осі обертання.

Момент цієї сили відносно точки О буде:

,

де - відстань елемента маси від осі обертання.

Сума моментів цих сил буде:

.

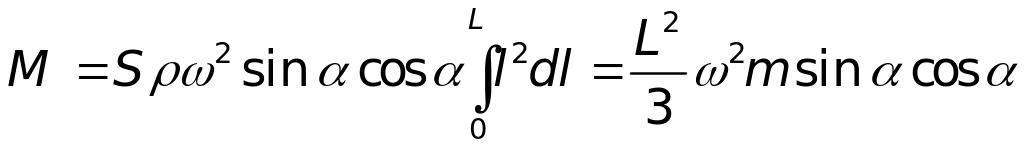В розглядуваній системі координат стержень знаходиться в стані спокою – момент сили інерції повинен дорівнювати моменту сили тяжіння 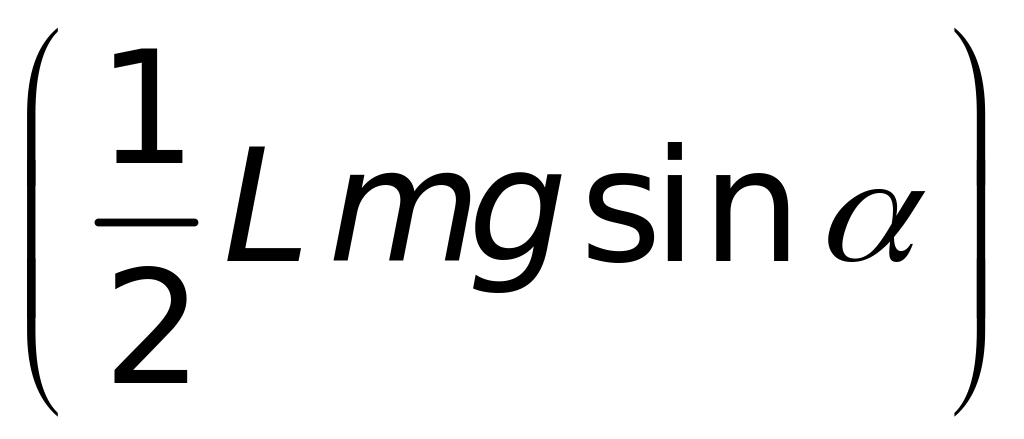. Рівність моментів сил дає:

.

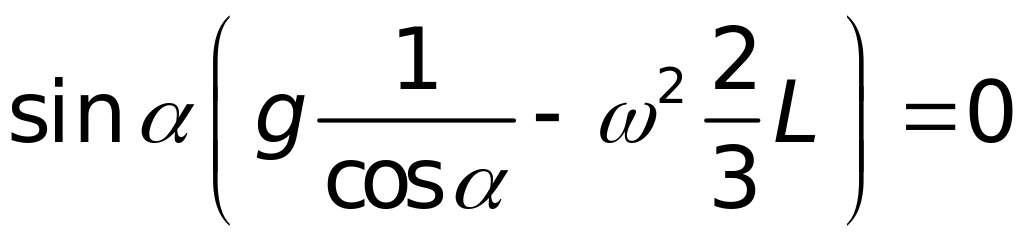Це рівняння для шуканої величини кута дає два розв’язки:

,

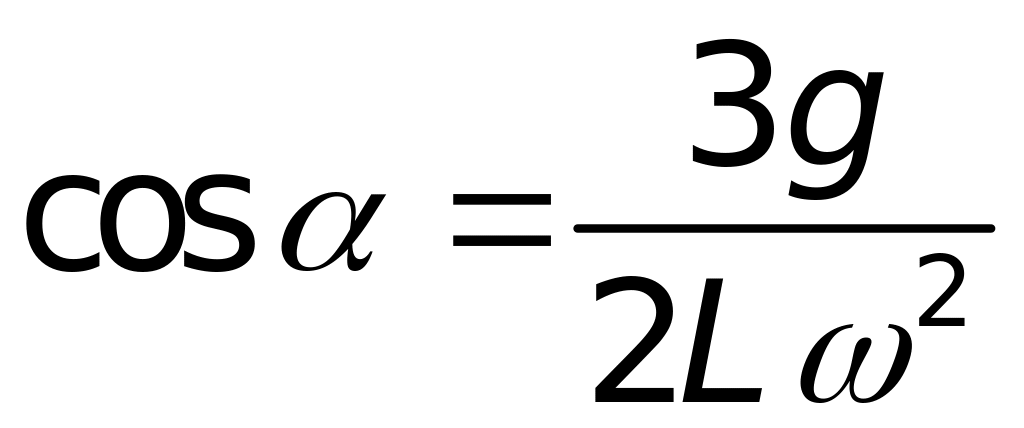Розв’язок не відповідає реальним умовам задачі (нестійкий рух).

В інерціальній системі відліку обертання стержня можна розглядати як рух конічного фізичного маятника. Його рух в цьому випадку можна звести до руху також конічного, але математичного маятника. Періоди коливань математичного маятника і стержня повинні дорівнювати:

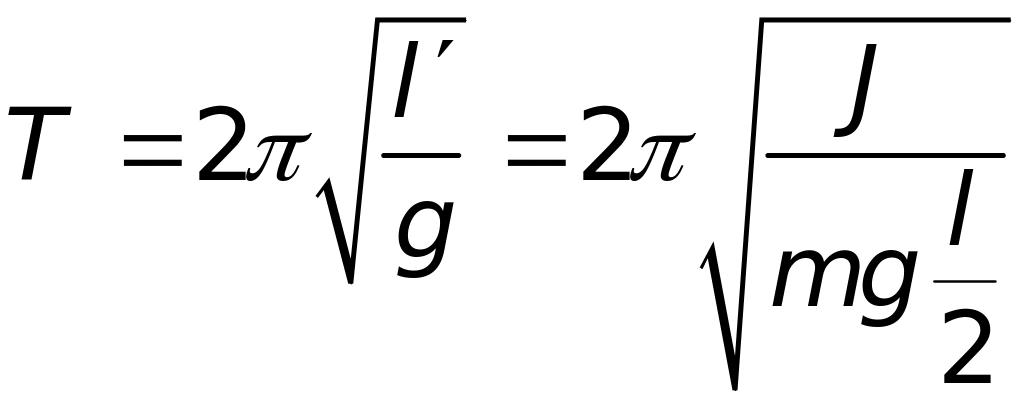
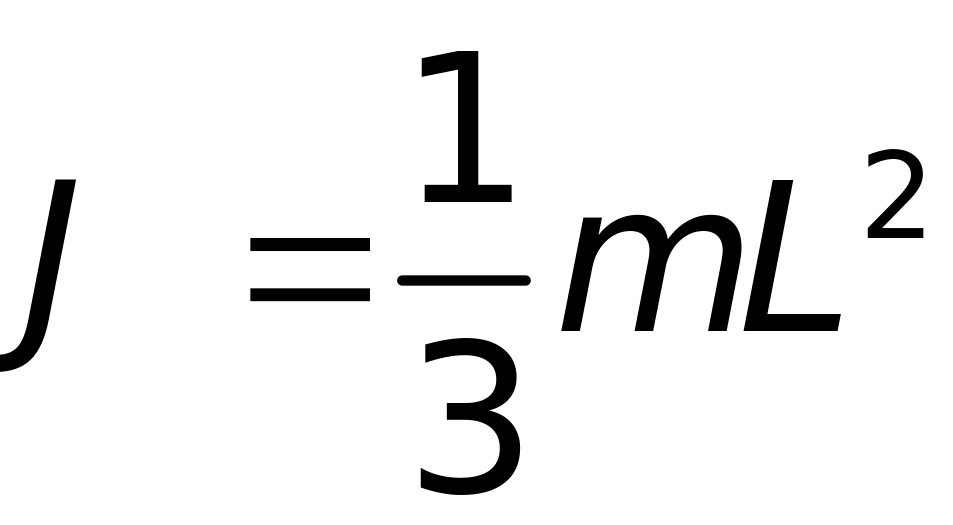де - довжина математичного маятника, - момент інерції стержня відносно точки О.

Для величини (відстань від точки прикладання сумарної доцентрової сили, що діє на стержень, до точки О) одержимо:

.

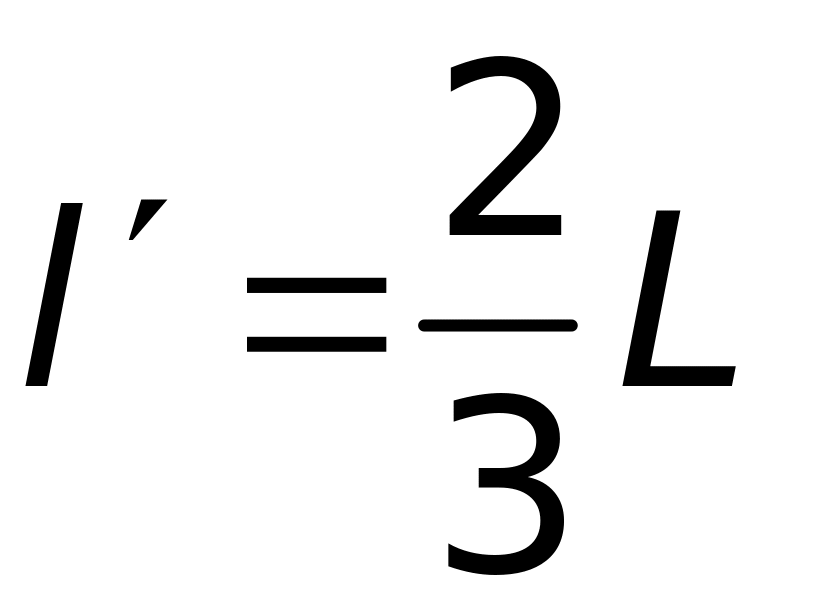Для радіуса обертання цієї точки маємо:

.

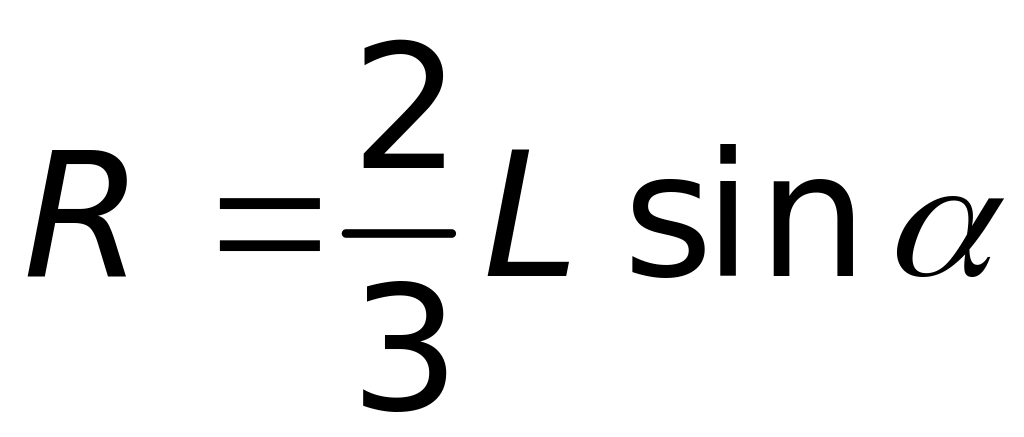Рівняння руху стержня буде:

.

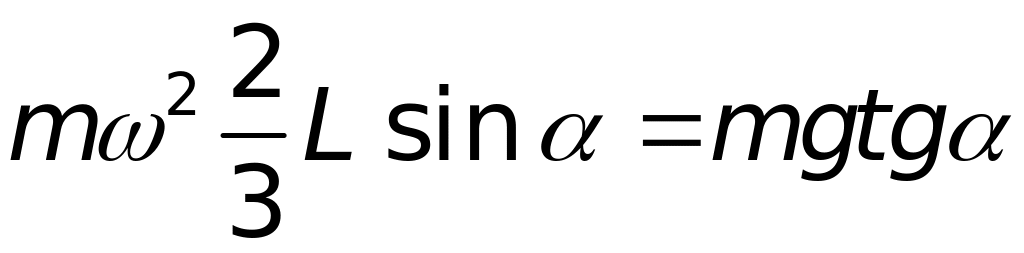або, як і раніше:

.

Приклад 5.8. Обертання Землі навколо своєї осі викликає відхилення поверхні води в ріці від її горизонтального положення. Визначити, біля якого берега і на яку величину рівень води буде вищий. Ріка тече в північній півкулі з півночі на південь. Ширина річки , швидкість течії , широта місцевості , кутова швидкість обертання Землі . Відцентровою силою інерції знехтувати.

Розв’язок. 1. В неінерціальній системі відліку, пов’язаною із Землею, крім сили тяжіння необхідно врахувати силу інерції Коріоліса:

Рівняння руху для частинки води буде:

,

Рис. 5.8

де - маса частинки, - прискорення частинки, - прискорення сили тяжіння. Результуюча цих двох сил буде перпендикулярна до лінії рівня води. З рис. 5.8 видно, що

.

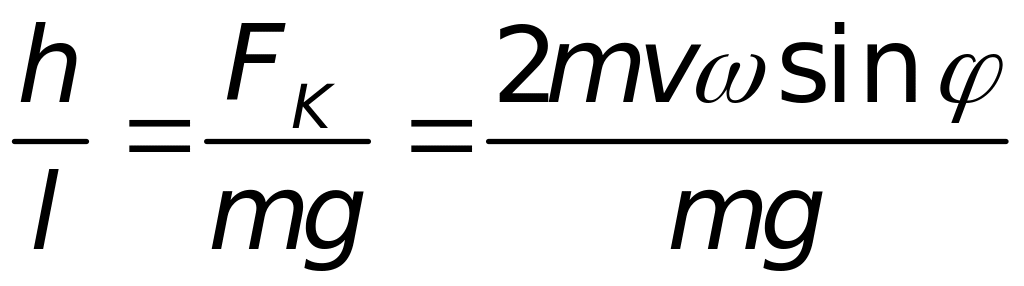Рівень води буде вищим біля правого берега річки на величину, яка визначається з останнього рівняння.

Маємо:

.

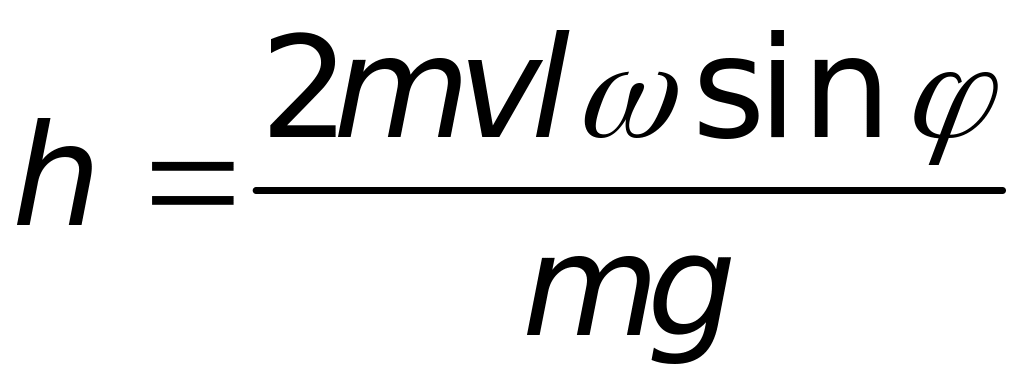2. В інерціальній системі відліку рух частинок води слід розглядати як складний, що складається одночасно з відносного і переносного рухів. Першим є рух по меридіану зі швидкістю . Переносний рух зумовлений обертанням Землі з кутовою швидкістю . Різниця рівнів води пояснюється впливом правого берега ріки.

Для рівняння руху в цьому випадку маємо

де - прискорення відносного руху, - прискорення Коріоліса.

Рис. 5.9

Приклад 5.9. На Землі, що обертається навколо своєї осі з кутовою швидкістю по екватору зі сходу на захід, з відносною швидкістю рухається поїзд маси . Не враховуючи сил тертя, вважаючи поїзд єдиним твердим тілом, визначити силу, що діє на поїзд з боку рейок (реакцію зв’язку) .

Розв’язок. 1. В неінерціальній системі координат кім звичай них сил взаємодії, а саме сили тяжіння поїзда і реакції зв’язку , необхідно враховувати відцентрову силу інерції і силу інерції Коріоліса . Для рівняння руху маємо:

,

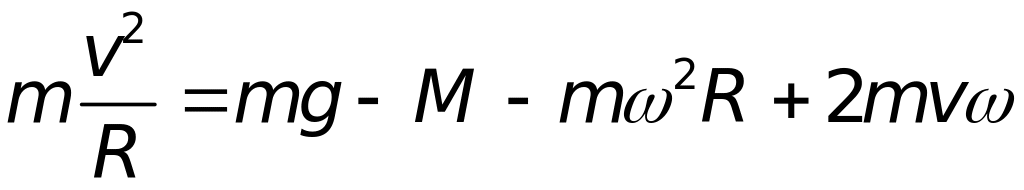де - радіус Землі.

Для шуканої величини одержимо:

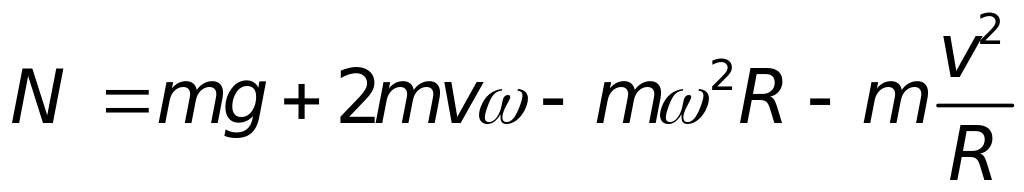
2. В інерціальній системі відліку рух слід розглядати як складний з відносною швидкістю і переносною . Повне прискорення в цьому випадку буде:

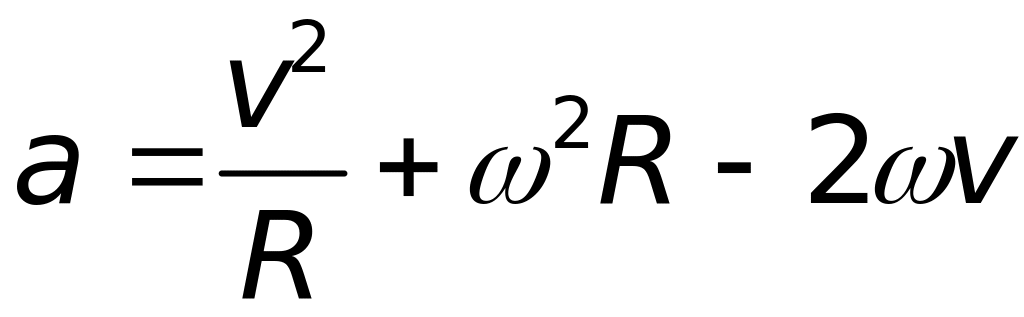
Для рівняння руху в цьому випадку маємо

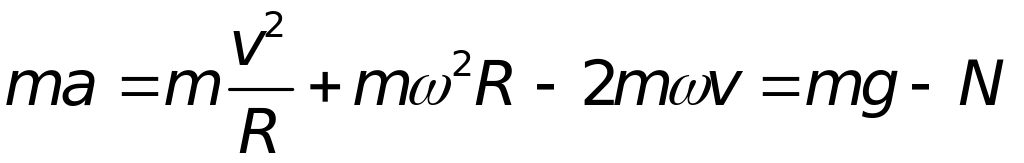
З цього рівняння, як і в попередньому випадку, одержимо: