2.3 Приклади розв’язування задач.

Приклад 2.1. На кінцях нитки, перекинутої через блок, висять на однаковій висоті дві гирьки масою по г кожна. Якщо на одну з гирьок покласти додатковий вантаж, вся система прийде в рух і через с відстань між гирьками стане рівна м. Визначте прискорення тіл, масу додаткового вантажу, силу натягу нитки , силу тиску додаткового вантажу на гирьку під час руху і силу тиску на вісь блока. Нитку можна вважати невагомою і нерозтяжною, масою блока знехтувати, тертя в блоці не враховувати.

Розв’язок: В задачі потрібно визначити всі внутрішні сили, що діють між окремими тілами системи. Систему слід уявно розділити на частини в тих місцях, де потрібно знайти ці сили, замінити дію в’язів силами і розглянути рух кожного тіла зокрема. В результаті задача зведеться до задачі динаміки матеріальної точки.

Рис. 2.2

Нехтуючи масою нитки, порівняно з масами вантажів, можна прийняти їх рух за рівноприскорений. Якщо не враховувати розтяг нитки, можна вважати, що в кожний момент часу вантажі на її кінцях мають однакові за модулем прискорення. Умова про відсутність тертя у блоці дозволяє вважати, що сили натягу нитки в будь-якому її перерізі однакові.

Виконуємо схематичний рисунок (рис.2.2). Зображаємо кожне тіло окремо і розкладаємо прикладені до нього сили. На ліву гирьку з боку Землі діє сила тяжіння, рівна , з боку нитки – сила натягу нитки . За умовою задачі під дією прикладених сил ця гирька піднімається вгору з прискоренням , тому . Проектуючи сили і прискорення на вісь, що має однаковий напрям з прискоренням, складаємо рівняння другого закону Ньютона в проекціях:

(1)

На додатковий вантаж діє з боку Землі сила тяжіння, що дорівнює , і з боку нижньої гирьки нормальна реакція опори . Під дією прикладених сил додатковий вантаж рухається вниз з прискоренням , тому . Проектуючи сили і прискорення на вісь, напрямлену так само, як прискорення додаткового вантажу, складаємо рівняння другого закону Ньютона в проекціях:

(2)

(Зверніть увагу: додатній напрям осі кожного з розглядуваних тіл системи різний. Його зручно вибирати в напрямку вектора прискорення тіл).

На праву гирьку діють: сила тяжіння, рівна , сила натягу нитки і сила нормального тиску додаткового вантажу. (Тут часто допускають помилку, вважаючи, що зверху на гирьку діє не сила нормального тиску , а сила тяжіння додаткового вантажу, рівна ). Під дією прикладених сил права гирька опускається вниз з прискоренням , тому .

Проектуючи сили і прискорення на вісь, що напрямлена так само як і прискорення цієї гирьки, складаємо рівняння другого закону Ньютона в проекціях:

. (3)

На блок діють сили натягу нитки (вниз) і нормальна реакція опори з боку осі (вгору) Під дією цих сил блок знаходиться в рівновазі, його прискорення рівне нулю, отже,

(4)

Накінець, використовуючи задані характеристики руху, складаємо кінематичне рівняння для однієї з гирьок, враховуючи, що за вказаний час кожна з них проходить відстань :

(5)

Система рівнянь (1) – (5) містить п’ять невідомих: , які нам потрібно знайти.

Розв’язуючи рівняння (1) – (5) відносно цих величин і підставляючи числові значення, одержимо:

м/с²;

кг;

Н;

Н;

Н.

Приклад 2.2. На столі лежить кубик масою . До кубика прикріплений ідеально гладкий ланцюжок, що звішується зі столу. До вільного кінця ланцюжка підвішений вантаж масою . Залишена сама на себе, система починає прискорено рухатись. Визначте натяг в середині ланцюжка в той момент, коли зі столу звисає 2/3 ланцюжка. Коефіцієнт тертя між кубиком і поверхнею стола дорівнює , маса ланцюжка .

Розв’язок: За умовою задачі потрібно визначити внутрішню силу, що діє під час руху між половинками ланцюжка, тому систему потрібно «розрізати» в середині ланцюжка і розглянути рух кожної з отриманих частин системи окремо.

Рис. 2.3

Виконуємо схематичний рисунок (рис. 2.3 а), вказуємо на ньому вектор прискорення в той момент, коли зі столу звішується 2/3 ланцюжка. Рух системи буде нерівномірно прискореним, що зростає з часом, оскільки за рахунок переміщення ланцюжка сила тяжіння в напрямку руху зростає.

Малюємо обидві частини окремо і розставляємо прикладені до них зовнішні сили (Рис. 2.3 б). На кубик і верхню половину ланцюжка діють сила тяжіння кубика, що рівна , сила тяжіння горизонтальної частини ланцюжка, що дорівнює (тут ), сила тяжіння частини ланцюжка, що звисає, дорівнює , сила тертя , реакції стола і , сила натягу (з боку нижньої половини ланцюжка). Під дією цих сил кубик і половина ланцюжка мають в даний момент часу прискорення , що напрямлене в бік руху. Згідно другого закону динаміки для цієї частини системи будемо мати:

Якщо заданий коефіцієнт тертя (або його потрібно знайти), то силу тертя потрібно представити в розгорнутому вигляді: (оскільки в даному випадку ) – і переписати основне рівняння більш детально:

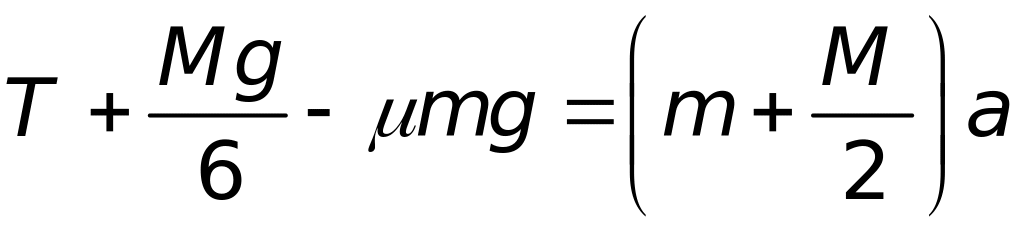(1)

До вантажу і другої половини ланцюжка прикладені сили тяжіння, рівні відповідно і , і сила натягу , що діє з боку верхньої половини ланцюжка. За умовою задачі ця частина розглядуваної системи опускається вниз з прискоренням , тому, проектуючи сили і прискорення на вісь, напрямлену так само як і прискорення, рівняння другого закону Ньютона в проекціях запишемо так:

(2)

Система рівнянь (1)-(2) містить дві невідомих величини і . Розв’язуючи їх відносно шуканого невідомого – сили натягу, що діє в середині ланцюжка, отримуємо:

Приклад 2.3. У вагоні, що рухається горизонтально зі сталим прискоренням м/с², висить на дротині вантаж масою кг. Визначити силу натягу дротини і кут її відхилення від вертикалі, якщо вантаж нерухомий відносно вагона.

Рис. 2.4

Розв’язок: На вантаж діють сила тяжіння і сила натягу дротини (рис. 2.4 ). Оскільки вантаж нерухомий відносно вагона, його прискорення дорівнює прискоренню вагона. При цьому нитка повинна бути відхилена від вертикалі назад, оскільки тільки в цьому випадку рівнодійна сил і буде напрямлена вперед, надаючи вантажу прискорення . Другий закон Ньютона у векторній формі матиме вигляд:

Проектуючи вектори , і на осі та , одержимо відповідно два скалярних рівняння:

Розв’язок системи рівнянь і підстановка числових значень дають:

,

,

Приклад 2.4. Вантаж масою кг обертається на канаті довжиною м в горизонтальній площині, здійснюючи об/хв. Який кут з вертикаллю утворює канат і яка сила його натягу?

Рис. 2.5

Розв’язок: На вантаж діють сила тяжіння і сила натягу каната . Згідно другого закону Ньютона

(1)

Оскільки рух по колу відбувається в даному випадку зі сталою за модулем швидкістю, то повне прискорення тіла є нормальне прискорення , напрямлене до центра кола радіуса :

Виберемо осі і так, щоб одна з них була напрямлена в бік прискорення. Проектуючи вектори, що входять в рівняння (1) на ці осі, отримаємо:

(2)

(3)

З рисунка видно, що . Розв’язавши рівняння (2), (3) з урахуванням останнього рівняння, маємо:

; .

Підставивши числові значення, маємо:

кн., , .

Приклад 2.5. У вагоні закріплено висок (кулька масою на нитці). Який напрям прийме висок, коли вагон буде скочуватися без тертя з похилої площини, що утворює з горизонтом кут ? Вважати, що висок нерухомий відносно вагона.

Рис. 2.6

Розв’язок: Припустимо, що висок складає з нормаллю до похилої площини шуканий кут . На кульку діють сила тяжіння і сила натягу нитки. За другим законом Ньютона

(1)

де - прискорення кульки, рівне прискоренню вагона. Оскільки вагону надає прискорення складова сили тяжіння, напрямлена вздовж похилої площини і рівна , де - маса вагона, то, за другим законом Ньютона, прискорення вагона

, (2)

Виберемо вісь проекцій , направивши її вздовж прискорення . Тоді замість векторного рівняння (1) з урахуванням (2) отримаємо

Звідси

(3)

Оскільки (одна сила тяжіння не може надати кульці прискорення ), то з (3) маємо:

, .

Таким чином, при спуску вагона висок розташований по нормалі до похилої площини.

Приклад 2.6. Визначити прискорення і , з якими рухаються вантажі і в установці, зображеній на рис. 2.7, а також силу натягу нитки. Тертям і масою блока знехтувати. Нитку вважати невагомою і нерозтяжною.

Рис. 2.7

Розв’язок: На вантаж діють сили тяжіння і сила натягу нитки, на вантаж - сила тяжіння і сили натягу , ниток. При цьому . Оскільки всі сили напрямлені по вертикалі, запишемо рівняння, що виражають другий закон Ньютона застосовані до вантажів зразу в скалярному вигляді, вибравши додатним напрям вниз і припустивши, що прискорення вантажу напрямлене вниз і, отже прискорення вантажу - вгору:

(1)

(2)

Розглядаючи кінематичну схему установки і враховуючи умову не розтяжності нитки, запишемо співвідношення між модулями переміщень вантажів, що відбуваються за один і той самий час: . Очевидно, таке ж співвідношення існує і між модулями прискорень вантажів:

(3)

Розв’язавши рівняння (1), (2), (3), отримаємо:

;

;

.

Звідси випливає:

1) якщо , то , , тобто, прискорення вантажів напрямлені так, як ми і припустили;

2) якщо , то - вантажі знаходяться в стані спокою або рухаються рівномірно;

3) якщо , то , . В цьому випадку прискорення вантажу напрямлене вгору, прискорення вантажу - вниз.

Зауваження: В усіх трьох випадках напрямки швидкостей вантажів залишаються невизначеними, оскільки вони залежать від напрямку початкових швидкостей і часу руху. Наприклад, при вантаж може рухатися прискорено вниз або сповільнено вгору. В обох випадках вектор напрямлений вниз.

Приклад 2.7. Візок масою кг, на якому лежить вантаж масою кг, тягнуть з силою , напрямленою горизонтально (рис. 2.8). Коефіцієнт тертя між вантажем і візком . Нехтуючи тертям між візком і опорою, знайти прискорення візка і вантажу , а також силу тертя між вантажем і візком у двох випадках:

1) Н,

Рис. 2.8

2) Н.

Розв’язок: Розглянемо сили, що діють на обидва тіла. При цьому, оскільки їх прискорення напрямлені по горизонталі, достатньо враховувати тільки ті сили, що діють горизонтально, оскільки інші, напрямлені вертикально – урівноважуються.

На візок діють сила і сила з боку вантажу . Остання напрямлена проти швидкості візка відносно вантажу при терті ковзання або проти сили при терті спокою, тобто в будь-якому випадку сила напрямлена вліво (рис. 2.8). На вантаж діє сила тертя з боку візка , напрямлена згідно третього закону Ньютона, вправо, причому за модулем . Спрямуємо вісь проекцій в бік прискорення, тобто по горизонталі вправо, запишемо в скалярному вигляді рівняння руху візка і вантажу:

(1)

(2)

Рівняння (1) і (2) містять три невідомих. Щоб отримати ще одне рівняння, з’ясуємо характер сили тертя між візком і вантажем. Якщо візок висковзує з-під вантажу, то між ними діє сила тертя ковзання, що дорівнює . Оскільки в даному випадку сила рівна за модулем силі тяжіння вантажу, то

(3а)

Якщо ж візок і вантаж рухаються як одне ціле, то між ними діє сила тертя спокою . Однак в цьому випадку виконується рівність

(3б)

Таким чином в обох можливих випадках отримаємо систему трьох рівнянь.

Отже, необхідно вияснити характер сил тертя, що діють між тілами. Розглянемо детальніше обидва варіанти:

а) візок висковзує з-під вантажу. Між ними діє сила тертя ковзання, яку знайдемо за формулою (3а):

.

б) візок і вантаж рухаються як єдине ціле, утримуючись тертям спокою. Тоді, позначивши , запишемо систему рівнянь (1), (2) у вигляді:

.

Розв’язавши цю систему, отримаємо

(4)

(5)

Формула (5) виражає пропорційну залежність між і . Однак, значення має границю, рівну , яка вже знайдена. Тому в дійсності два тіла будуть рухатись як єдине ціле тільки при таких значеннях сили , при яких значення , що визначається з (5), не буде перевищувати її граничного значення. Здійснивши розрахунки, одержимо:

1. якщо , то Н;

2. якщо , то 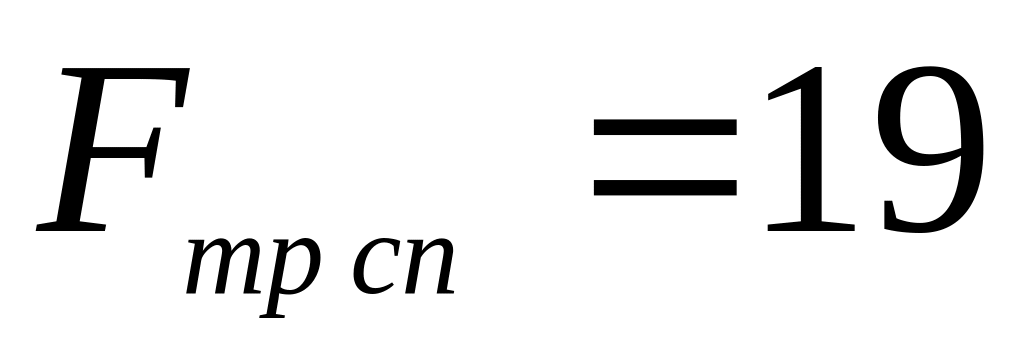Н, що неможливо, оскільки граничне значення Н. Отже, в цьому випадку між тілами діятиме тертя ковзання.

Тепер легко дати відповідь на всі питання задачі:

1) . Між тілами діє сила тертя спокою Н. З формули (4) знаходимо м/с²;

2) . Між тілами діє сила тертя ковзання Н. З (1) і (2) знаходимо прискорення тіл: м/с², м/с².

Приклад 2.8. На вершині двох похилих площин, що утворюють з горизонтом кути і , закріплено блок (рис. 2.9). Вантажі кг і кг з’єднані ниткою, перекинутою через блок. Визначити прискорення , з яким почнуть рухатись вантажі вздовж похилих площин, і силу натягу нитки. Коефіцієнти тертя вантажів об площини рівні між собою: . Блок і нитки вважати невагомими, тертя в осі блока не враховувати. Розглянути випадки:

1) ;

2) .

Рис. 2.9

Розв’язок: На кожен з вантажів діють чотири сили: сила тяжіння, сила нормального тиску опори, сила тертя і сила натягу нитки. В цій задачі ми не знаємо напрямків сил тертя і, отже, не можемо зразу приступити до складання рівнянь руху вантажів в скалярній формі. Дійсно, сила тертя напрямлена завжди в бік, протилежний до відносної швидкості рухомого тіла. Але куди рухаються вантажі – невідомо.

Скористаємось тим правилом, що сила тертя, яка виникає при русі тіла, не може змінити напряму його відносної швидкості. З’ясуємо напрям руху вантажів, припустивши, що тертя відсутнє. Оскільки в цьому випадку прискорення вантажів визначається різницею складових сил тяжіння, напрямлених вздовж відповідних площин, то знайдемо ці складові:

Н,

Н

Оскільки , то вантаж рухатиметься по похилій площині вгору, вантаж - вниз. А оскільки сили тертя не можуть змінити напрям руху тіл, то і при наявності сил тертя вантажі рухатимуться так само.

Тепер приступимо до складання рівнянь руху вантажів. Вибравши для кожного вантажу осі проекцій і так, щоб одна з осей була напрямлена вздовж прискорення (рис. 2.9), запишемо для кожного вантажу і в проекціях на осі відповідно по два скалярних рівняння (враховуючи при цьому, що )

(1)

(2)

Крім того, за законом ковзання,

(3)

Систему рівнянь (1) – (3) з невідомими перетворимо в систему з двох рівнянь:

(4)

в якій два невідомих: і . Розв’язавши цю систему, одержимо:

(5)

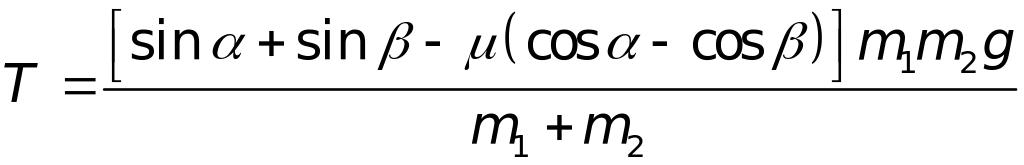(6)

Підклавши в формули (5) і (6) числові дані для першого випадку ( ), отримаємо:

м/с², Н.

Для другого випадку ( ) з формули (5) маємо

м/с².

Перш ніж виконувати подальші розрахунки, проаналізуємо отриманий результат. Від’ємне значення прискорення показує, що при напрямки руху вантажів протилежні тим, що були б при відсутності тертя (при цьому враховуємо, що в обох випадках початкові швидкості вантажів рівні нулю). Але це неможливо, оскільки сила тертя не в стані змінити напрям руху тіла. Таким чином, отримано неправильний результат для прискорення. Отже, система рівнянь (1) – (3) не відповідає дійсності при . Єдиною помилкою, яку ми могли тут допустити, є припущення про те, що вантажі знаходяться в стані руху і між ними і площинами діють сили тертя ковзання (це вказано в рівняннях (3)). Отже, в дійсності при вантажі знаходяться в стані спокою і утримуються силами тертя спокою, для яких співвідношення (3) не виконуються. Отже, при .

Тепер замість системи (4) отримаємо систему

В якій невідомі , , і яка, очевидно, не має єдиного розв’язку для . Задача стала невизначеною: величина тепер залежить від деяких додаткових обставин, що не вказані в умові, а саме від того, яким чином вантажі були поміщені в положення, зображене на рис. 2.9.