3.2 Кинематический анализ

Число возможных уравнений статики для расчета фермы - 2У (два уравнения статики для каждого узла). Количество неизвестных при расчете фермы - С+С₀. Здесь У –число узлов фермы; С – число стержней; С₀ – число опорных связей. Тогда условие статической определимости фермы будет иметь следующий вид 2У=С+С₀ (число уравнений = числу неизвестных).

В других случаях, если условие не выполняется:

2У>С+С₀ - система геометрически изменяема;

2У<С+С₀ - система статически неопределима.

3.3 Узловая передача нагрузки

Н

F=ql

агрузка от перекрытий, передаётся на узлы ферм через специальные балки (прогоны). Тогда значение узловой нагрузки в средних узлах фермы будет qd, а для крайних узлов -

q

F

F

F

d

d

d

d

d

d

F

F

3

4

5

F/2

F/2

2

1

h

A

B

h₁

6

7

8

H_A=0

d

d

d

d

d

d

V_B=3F

а)

б)

Рис. 3.8

3.4 Аналитический расчёт ферм на постоянную нагрузку

Прежде чем производить расчёт фермы, необходимо определить опорные реакции (исключение составляют консольные фермы). В ферме, показанной на рис. 3.8 горизонтальная реакция H_A=0 (из уравнения статики ). Так как ферма симметрична и нагрузка на неё также симметрична, вертикальные реакции V_А и V_В равны. Для их определения суммируем все внешние силы и полученное значение делим пополам:

Если в ферме имеет место узловая нагрузка, то все стержни работают только на сжатие или растяжение. То есть в стержнях фермы возникает только продольная сила. Будем обозначать эту продольную силу N_i-j, где i и j узлы, которые соединяет стержень. Задача расчёта заключается в определении продольных сил N_i-j в стержнях фермы.

Способ вырезания узлов.

Так как все силы, действующие на узел, пересекаются в одной точке, то для каждого узла плоской фермы можно составить два уравнения равновесия, выражающие равенство нулю суммы проекций всех сил на горизонтальную и вертикальную оси. Этот способ используется, если в узле фермы 2 неизвестных усилия. Вся статически определимая ферма может быть рассчитана последовательным вырезанием узлов. Проследим это на примере фермы, показанной на рис. 3.8. Вырежем узел A , т.к. в нём соединяются 2 стержня. Используем уравнения статики:

; N_A-6 =0.

N_A-1+3F=0, N_A-1=-3F.

(Стержень сжат)

а)

Далее можно вырезать узел 1 и определить усилия N_1-2 и N_1-6.

; N_1-6∙ cos α+N_1-2∙ cos β =0.

-N_1-6∙ sin α+N_1-2∙ sin β -N_1-A -F/2 =0

Решаем систему уравнений относительно N_1-6 и N_1-2

Далее можно вырезать узлы 2, 6, 3, 7, 4, 8.

1

F/2

N_1-2

N_1-6

N_1-A

β

α

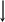
б)

Рис. 3.9