2. Погрешности измерений

Наиболее широко в метрологической практике использует­ся первое свойство — точность измерений. Рассмотрим его наи­более подробно. Точность измерений СИ определяется их по­грешностью.

Погрешность — это разность между показаниями СИ и ис­тинным (действительным) значением измеряемой физической величины. Следует делать различие между понятиями «погрешность» и «ошибка». Первая возникает по объективным обстоятельствам, устранить ее невозможно, можно уменьшить с помощью определенных методов. Термин «ошибка» свя­зан с субъективными обстоятельствами. После проверки результатов ее устраняют.

По закономерностям проявления погрешности делят на систематические, случайные и промахи.

Систематические погрешности измерения — составляющие погрешности измерения, которые остаются постоянными или закономерно изменяются при повторных измерениях одной и той же величины. Закономерно изменяющиеся систематические погрешности, в свою очередь, подразделяются на прогрессирующие (возрастаю­щие, убывающие), периодические и изменяющиеся по сложному непериодическому закону.

К постоянным систематическим погрешностям относят погреш­ность градуировки шкалы, погрешность, обусловленную неточностью подгонки значения меры, температурную погрешность и др.

К переменным систематическим погрешностям относят погрешность, обусловленную нестабильностью напряжения источника питания, влиянием электромагнитных полей и других влияющих величинах

Анализ возможных причин появления систематических погрешностей, способы обнаружения и устранения их влияния на резуль­тат измерения — одна из основных задач каждого точного измере­ния. Обнаружение систематических погрешностей представляет собой сложную задачу, но если погрешности обнаружены, то обычно удается их оценить и устранить. Систематические погрешности можно исключить теоретическим анализом; поверкой прибора перед его применением в аналогичных условиях; предварительной калиб­ровкой, установкой нуля; несколькими проведенными измерениями по различным методикам; использованием метода замещений; осу­ществлением компенсации знака погрешности. В случаях, когда значение систематической погрешности может быть достаточно точно определено, вводят поправку или поправочный множитель.

Поправка — значение величины, одноименной с измеряемой, прибавляемое к полученному при измерении значению величины с целью исключения систематической погрешности.

Поправочный множитель — число, на которое с целью исключе­ния систематической погрешности умножают результат измерения.

Полностью устранить систематические погрешности нельзя. Уменьшение влияния систематической погрешности может быть за счет перевода систематической погрешности в случайную.

Случайные погрешности измерений — составляющие погрешно­сти измерения, изменяющиеся не по определенному закону, а слу­чайным образом (по зна­ку и значению) при повторных измерениях одной и той же вели­чины с одинаковой тщательностью. Значение и знак случайной погрешности определить невоз­можно, так как случайные погрешности обязаны своим происхож­дением причинам, действие которых неодинаково в каждом экспе­рименте и не может быть учтено. Обнаруживаются случайные по­грешности при многократных измерениях одной и той же величины, поэтому их влияние на результат измерения учитывается методами математической статистики и теории вероятностей. При многократном и достаточно точ­ном измерении они порождают рассеяние результатов.

Характеристиками рассеяния являются средняя квадратическая погрешность и раз­мах результатов измерений. Поскольку рассеяние носит вероят­ностный характер, то при указании на значения случайной по­грешности задают вероятность.

Средняя квадратическая погрешность (среднее квадратическое отклонение (S_δ) — характеристика рассеяния результатов измере­ний одной и той же величины вследствие влияния случайных по­грешностей. Применяется для оценки точности первичных и вто­ричных эталонов. Она представляет среднюю квадратическую погрешность ре­зультата измерений, состоящую из случайных и неисключенных систематических погрешностей.

Показатели точности могут устанавливаться в связи с группировкой погрешностей СИ по условиям измерения.

Промахи — погрешности, которые явно и резко искажают ре­зультат измерений — следствие неправильных действий экспери­ментатора, неисправностей в схемах и приборах.

В зависимости от условий возникновения погрешности подразделяют на основную и дополнительную.

Основная погрешность — погрешность средств изме­рений, используемых в нормальных условиях, т. е. при нормальном положении, температуре окружающей сре­ды 20±5° С, отсутствии внешнего электрического и маг­нитного полей, кроме земного, и т. п.;

Дополнительная погрешность – это погрешность средств измерений, возникающая в ре­зультате отклонения значения одной из влияющих вели­чин (температуры, относительной влажности, напряжения сети переменного тока и пр.) от нормального значения. Иными словами, это погрешность, возникающая при отклонении условий экс­плуатации от нормальных.

Обычно метрологические характеристики нормируют раздель­но для нормальных и рабочих условий применения СИ. Нормаль­ными считаются условия, при которых изменением характеристик под воздействием внешних факторов (температура, влажность и пр.) принято пренебрегать. Так, для многих типов СИ нормальны­ми условиями применения являются температура (293 ± 5) К, ат­мосферное давление (100 ± 4) кПа, относительная влажность (65 ± ± 15)%, электрическое напряжение в сети питания 220 В ± 10%. Ра­бочие условия отличаются от нормальных более широкими диапа­зонами изменения влияющих величин. И те и другие метрологичес­кие характеристики указываются в НД.

По характеру изменения различают аддитивные (от лат. additivus — при­бавляемый) и мультипликативные (от лат. multipico — умно­жаю) погрешности.

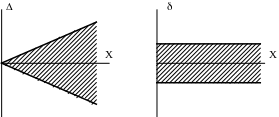
А ддитивные погрешности - погрешности, абсолютная величина Δ которых не зависит от значения измеряемой величины Х. Например, если показание измерительного прибора при отсутствии входного сигнала не равно нулю, то эта погрешность "установки нуля" Δ будет оставаться постоянной во всем диапазоне измерения прибора. При этом относительная погрешность δ "установки нуля" будет уменьшаться обратно пропорционально с ростом измеряемой величины.

Мультипликативные погрешности - погрешности, абсолютное значение ΔХ которых возрастает с увеличением значения измеряемой величины Х. Например, абсолютная погрешность счетчиков электрической энергии увеличивается с ростом его показаний. При этом относительная погрешность δ счетчика, которая характеризует точность измерения прибора, будет оставаться неизменной с ростом величины измеренной энергии. Другими словами, точность измерения не будет зависеть от того, когда сняты показания с прибора.

Абсолютная погрешность ΔX — это разность между измерен­ным Х и истинным Х_И значениями измеряемой величины. Абсо­лютная погрешность выражается в единицах измеряемой вели­чины.

Поскольку истинное значение измеряемой величины опреде­лить невозможно, вместо него на практике используют действи­тельное значение измеряемой величины Х_Д. Действительное зна­чение находят экспериментально, путем применения достаточно точных методов и средств измерений. Оно мало отличается от истинного значения и для решения поставленной задачи может использоваться вместо него. За действительное зна­чение обычно принимают показания высокоточных (образцовых) средств измере­ний Х₀. Таким образом, на практике абсолютную погрешность на­ходят по формуле:

ΔX = Х - Х₀

Относительная погрешность δ — это отношение абсолютной погрешности измерения к истинному (действительному) значению измеряемой величины (она обычно выражается в процентах):

Точность измерений СИ—качество измерений, отражающее близость их результатов к действительному (истинному) значе­нию измеряемой величины. Точность определяется показателя­ми абсолютной и относительной погрешности.

Однако в большей степени точность СИ характе­ризует относительная погрешность δ, т.е. выраженное в про­центах отношение абсолютной погрешности к действительно­му значению величины, измеряемой или воспроизводимой данным СИ.

В стандартах нормируют характеристики точности, связан­ные с другими погрешностями.

Относительная приведенная погрешность γ

где Х_Н - нормирующее значение, принимаемое равным величине, соответствующей размаху шкалы. Х_Н принимается равным Х_К (конечному значению шкалы прибора), если нулевая отметка находится с краю шкалы, или арифметической сумме конечных значений диапазона измерений Х_К1 и Х_К2, если нулевая отметка находится внутри шкалы. Если шкала нелинейная (гиперболическая, логарифмическая и т.п.), то нормирующее значение равно длине шкалы.

В зависимости от источника возникновения погрешности делят на на инструментальные, методические и субъективные.

Инструментальная погрешность — погрешность, присущая са­мому средству измерений, т. е. тому прибору или преобразова­телю, при помощи которого выполняется измерение. Причинами инструментальной погрешности могут быть неидеальность харак­теристики средства измерений, влияние окружающей среды на эту характеристику и т. п.

Методическая погрешность появляется вследствие несовер­шенства метода измерения: несоответствие измеряемой величины и ее модели, принятой при измерении; влияние средства измере­ний на объект измерения и процессы, происходящие в нем.

Номенклатура нормируемых метрологических характерис­тик СИ определяется назначением, условиями эксплуатации и многими другими факторами. У СИ, применяемых для высоко­точных измерений, нормируется до десятка и более метрологи­ческих характеристик в стандартах технических требований (технических условий) и ТУ. Нормы на основные метрологичес­кие характеристики приводятся в эксплуатационной докумен­тации на СИ. Учет всех нормируемых характеристик необхо­дим при измерениях высокой точности и в метрологической практике. В повседневной производственной практике широко пользуются обобщенной характеристикой — классом точности.