Билет 1

1 Вопрос - Системы статически определимые и неопределимые.

Если количество неизвестных реакций не превышает числа уравнений равновесия, то такая система называется “Статически определимой”.

Если же количество неизвестных больше, такая система называется “Статически неопределимой”.

3 Неизвестных, 2 уравнения

Эта задача 1 раз статически неопределима

2 Вопрос – импульс. Закон сохранения импульса

Количеством движения материальной точки называется вектор, равный произведению массы точки на ее скорость .

Количество движения точки в физике часто называют импульсом материальной точки.

Проекции количества движения точки на прямоугольные декартовы оси координат равны:

, ,

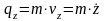
Единицей измерения количества движения в СИ является –

Элементарный и полный импульс силы.

Действие силы на материальную точку в течении времени можно охарактеризовать элементарным импульсом силы .

Полный импульс силы за время , или импульс силы , определяется по формуле . (Полный интеграл за время от элементарного импульса).

В частном случае, если сила постоянна и по величине , и по направлению ( ), .

Проекции импульса силы на прямоугольные декартовы оси координат равны:

Единицей измерения импульса в СИ является –

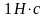
Закон сохранения импульса. До взаимодействия
После взаимодействия
Согласно 3 з-ну Ньютона:  , следовательно:
Геометрическая (векторная) сумма импульсов взаимодействующих тел, составляющих замкнутую систему, остается неизменной.

Геометрическая (векторная) сумма импульсов взаимодействующих тел, составляющих замкнутую систему, остается неизменной.

Примеры применения закона сохранения импульса:

1. Любые столкновения тел (биллиардных шаров, автомобилей, элементарных частиц и т.д.);

2. Движение воздушного шарика при выходе из него воздуха;

3. Разрывы тел, выстрелы и т.д.

Билет 2

1 Вопрос -Напряжения при растяжении (сжатии)

Растяжение или сжатие стержня вызывается силами, действующими вдоль его оси (рис.5.1,а). При этом в поперечных сечениях из шести внутренних силовых  факторов  возникает  только  один — продольная (осевая) сила N, эпюра которой приведена на рис.5.1,б. Осевая сила в сечении является равнодействующей нормальных напряжений, возникающих в каждой из точек сечения. Отсутствие поперечных сил дает основание предположить, что касательные напряжения в каждой точке поперечного сечения равны нулю.

а
б
в

Рис.5.1. Продольная сила в сечении и ее эпюра

Выведем формулу для определения нормальных напряжений. Рассечем стержень произвольным поперечным сечением n — n (рис.5.1,в). Статическая сторона задачи выражается уже известным соотношением

                                                                                                 (5.5)

Из (5.5) нельзя определить величину  , так как  закон распределения напряжений в точках  поперечного сечения не известен.

Рассмотрим геометрическую сторону задачи. При наблюдении деформации  растяжения   стержня,   на   поверхности   которого   нанесены линии, перпендикулярные к оси бруса (рис.5.1,а), можно отметить, что эти линии, смещаясь параллельно самим себе, остаются прямыми и перпендикулярными к оси бруса. Предполагая, что указанная картина перемещения сечений имеет место и внутри стержня,  приходим к гипотезе  плоских сечений: поперечные сечения стержня,  плоские до деформации, остаются плоскими и после нее, перемещаясь поступательно вдоль оси стержня.

Разобьем стержень на продольные (параллельные оси стержня) элементы бесконечно малых поперечных сечений и будем в дальнейшем называть ихволокнами. На основании гипотезы плоских сечений следует заключить, что все волокна удлиняются на одну и ту же величину и их относительные удлинения   одинаковы:

                                                                                           (5.6)

Это аналитическое выражение геометрической стороны задачи.

Физическая сторона рассматриваемой задачи заключается в установлении зависимости деформаций от напряжений. При упругих деформациях эта зависимость подчиняется закону Гука:

                                                                                                      (5.7)

где Е — модуль упругости первого рода.

Учитывая постоянство модуля упругости Е для однородного изотропного материала, а также (5.6) и (5.7), находим, что

                                                                                          (5.8)

Подставляя выражение (5.8) в (5.5), получаем

                                                          (5.9)

откуда

                                                                                                     (5.10)

Знак напряжения зависит от знака продольной силы в рассматриваемом сечении. В случае сжатия напряжения считают отрицательными. Формула (5.10) справедлива лишь для сечений, достаточно удаленных от мест приложения сосредоточенных нагрузок.

Определяя напряжения при растяжении, сжатии и других видах деформаций, широко пользуются положением, носящим название принципа Сен-Венана:если тело нагружается статически эквивалентными системами сил, т. е. такими, у которых главный вектор и главный момент одинаковы, и при этом размеры области приложения нагрузок невелики по сравнению с размерами тела, то в сечениях, достаточно удаленных от мест приложения сил, напряжения мало зависят от способа нагружения.

Общего теоретического доказательства принцип Сен-Венана не имеет, но его справедливость подтверждается многочисленными теоретическими и экспериментальными исследованиями.

Поясним этот принцип на следующем примере. Один и тот же стержень, закрепленный верхним концом, нагружается на свободном конце статически эквивалентными нагрузками, равнодействующие которых выражаются величиной вектора F. Нагрузки приложены различными способами: а) в виде сосредоточенной осевой силы; б) в виде двух сил; в) в виде распределенной нагрузки. Исследования показывают, что во всех случаях в поперечном сечении, удаленном на расстояние, превышающее в 1,5-2 раза его поперечные размеры, напряжения практически одинаковы. В сечениях же, расположенных близко от места приложения сил, величина напряжений и характер их распределений различны.

Перейдем к определению деформаций стержня. Из выражения (5.9) можно найти относительное удлинение

                                                                                                    (5.11)

В пределах призматического участка стержня длиной  , выполненного из однородного материала (Е = const), в сечениях которого действуют одинаковые продольные силы N, удлинение каждой единицы длины одинаково и, следовательно, абсолютное удлинение

                                                                                           (5.12)

Формула (5.12) выражает закон Гука для абсолютных удлинений.

Произведение EА в знаменателе (5.12) называется жесткостью при растяжении-сжатии и имеет размерность силы. Величину   называютжесткостью стержня.

Если на рассматриваемом участке продольная сила и поперечное сечение переменны (рис.5.2,а,б,в), то для элемента бесконечно малой длины (рис.5.2,г) ихна основании формулы (5.12)  можно записать так:

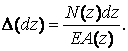
		а		б		в		г

Рис.5.2. Переменная по длине продольная сила

Полное удлинение участка длиной   получим, суммируя удлинения всех бесконечно малых участков:

                                                                                          (5.13)

Заметим, что перемещение некоторого сечения относительно другого равно продольной деформации участка стержня, заключенного между рассматриваемыми сечениями.

Растяжение и сжатие сопровождаются изменением перечных размеров стержня. При растяжении они уменьшаются, а при сжатии — увеличиваются.

По аналогии с продольной деформацией разность соответствующих поперечных размеров после деформации и до нее назовем абсолютной поперечной деформацией.

При растяжении поперечные деформации отрицательны, при сжатии — положительны.

Разделив абсолютную поперечную деформацию на соответствующий первоначальный размер, получим относительную поперечную деформацию. Относительная поперечная деформация   для изотропных материалов по всем поперечным направлениям одинакова.

Между поперечной   и продольной   относительными деформациями при простом растяжении и сжатии в пределах применимости закона Гука существует постоянное отношение. Абсолютная величина этого отношения носит название коэффициента Пуассона:

                                                                                                    (5.14)

Коэффициент Пуассона — безразмерная величина. Учитывая, что продольная и поперечная деформации всегда имеют противоположные знаки, получаем

,                                                                                                 (5.15)

или, согласно (5.7),

                                                                                                (5.16)

При сжатии напряжение в (5.16) следует подставлять со знаком минус.

Коэффициент Пуассона наряду с модулем упругости характеризует упругие свойства материала. Для всех изотропных материалов значения коэффициента Пуассона лежат в пределах  . В частности, для пробки    близок к нулю, для каучука — 0,5, для стали — 0,3.