4. Зональная система прямоугольных координат

Географические координаты могут быть распространены на всю поверхность земного эллипсоида. В этом их большое достоинство. Однако их применение в массовых геодезических работах затруднительно, поскольку оно связано со сложными вычислениями. Поэтому эти координаты применяют при картографировании, навигации, создании и использовании геоинформационных систем (ГИС) и т.д.

В инженерной геодезии в связи с этим используют плоские прямоугольные координаты. Для установления связи между географическими координатами любой точки на земном сфероиде и прямоугольными координатами той же точки на плоскости применяют специальный способ проектирования всего земного шара на плоскость по шестиградусным зонам, простирающимся от северного полюса к южному.

Счет зон ведут на восток от нулевого, проходящего через Гринвическую обсерваторию, меридиана. Каждую полученную таким образом зону проектируют поочередно на плоскость при помощи цилиндра.

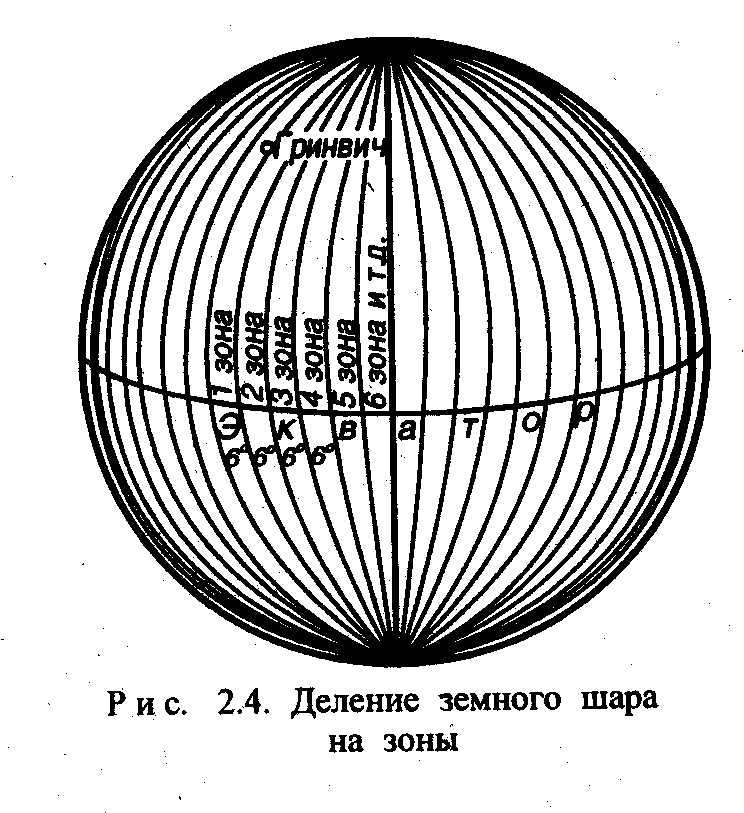
Если общую фигуру Земли представить в виде сферы, то ось АВ такого цилиндра будет проходить через центр сферы 0 (рис. 2.5). При этом ось вращения Земли PP₁ будет перпендикулярна оси цилиндра АВ, и каждая зона будет касаться поверхности цилиндра по своему среднему меридиану.

Каждую зону последовательно проектируют на внутреннюю боковую поверхность цилиндра при условии сохранения равенства углов, формы и подобия изображаемых контуров. Зоны переходят на поверхность цилиндра в несколько расширенном виде (см. рис. 2.5) и, развернув цилиндр, получают плоское изображение земной поверхности. Такую проекцию поэтому называют поперечно-цилиндрической (рис. 2.6). (иногда её называют системой прямоугольных координат Гаусса-Крюгнра). Она дает не сплошное изображение всей земной поверхности, а с разрывами, увеличивающимися от экватора к полюсам.

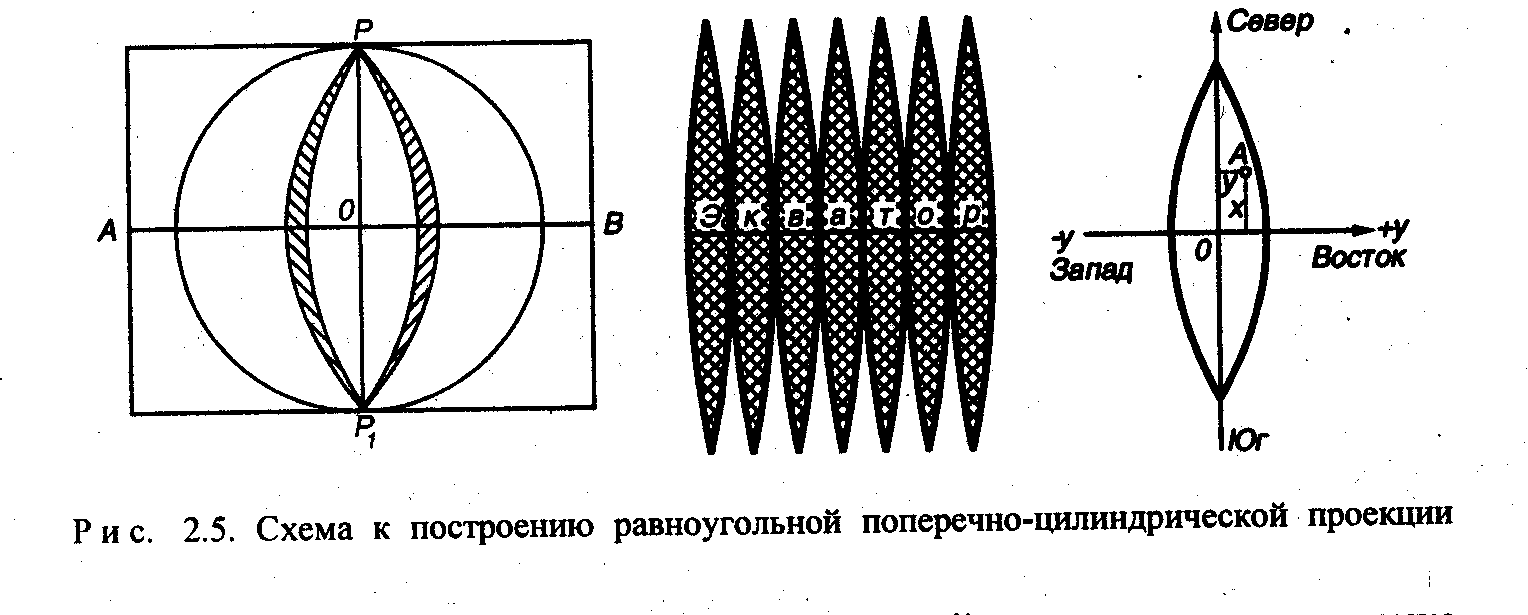
В этой системе начало координат в каждой зоне принимают в точке пересечения среднего меридиана с экватором (рис. 3). Средний меридиан зоны принимают за ось абсцисс, поэтому его называют еще осевым меридианом. Изображение экватора в виде прямой, перпендикулярной осевому меридиану, принимают за ось ординат.

Абсциссы к северу от экватора принимают положительными, а к югу — отрицательными. Ординаты, отсчитываемые на восток от осевого меридиана, считают положительными, а на запад — отрицательными.

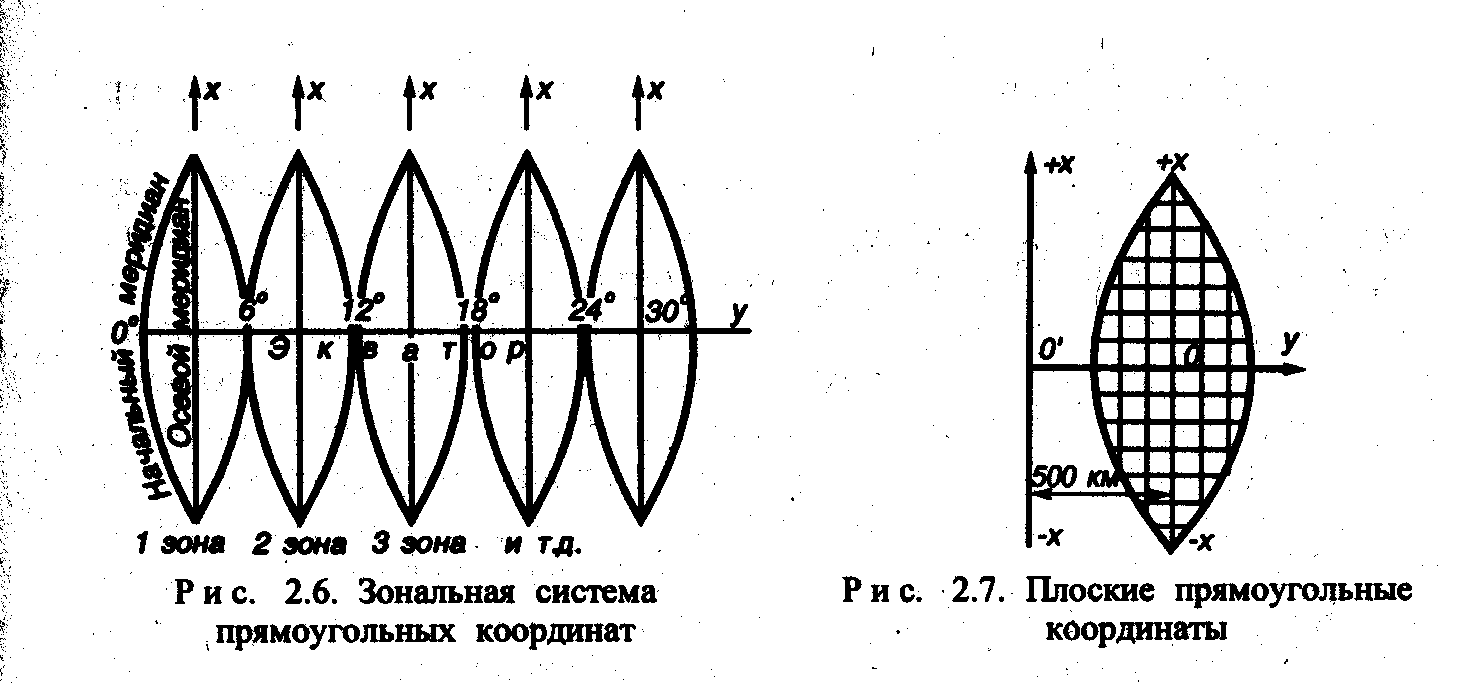
По экватору протяженность зоны с запада на восток примерно 666 км. Посередине проходит осевой меридиан, следовательно, раз зона составляет 6°, то от осевого меридиана до конца зоны протяженность составляет 333 км.

С тем чтобы в пределах каждой зоны иметь дело только с положительными значениями ординат, за ординату осевого меридиана принимают не ноль, а (+ 500 км) (рис. 4).

Поскольку в каждой зоне числовые значения ординат повторяются, то для того, чтобы по координатам точки можно было определить, к какой зоне она относится, к значению ординаты Y слева приписывается номер зоны. Такие координаты называются полными. Например, координаты объекта Х = 6346650 м, Y = 4522800 м означают, что он расположен к северу от экватора на расстоянии 6 346 650 м и к востоку от своего осевого меридиана 4-й зоны на расстоянии 22 800 м (52 2800м - 500 км = 22 800 м). Объект, который имеет ординату Y = 15323500 м расположен к западу от осевого меридиана 15-й зоны на 176 500 м (500 км –323500 м = 176 500 м).

Итак, Гаусс предложил поверхность земного эллипсоида разбить меридианами, которые отстоят друг от друга на 6⁰, на 60 равных зон. Приняв осевой (средний) меридиан в каждой зоне за ось Х , а экватор – за ось Y, а их пересечение – за начало координат, получим систему плоских прямоугольных координат Гаусса для данной зоны. Таким образом, каждая зона будет иметь свою систему координат. Вместе с тем, системы координат Гаусса и геодезическая взаимозависимые, поскольку ось Х соединяется с одним из меридианов, а ось Y – с экватором.

Координаты Х и Y измеряются в линейных величинах (метрах).

Для того, чтобы значительно упростить определение прямоугольных координат, на карте через целое число километров проводят прямые линии, параллельные осевому меридиану и экватору, поэтому прямоугольную координатную сетку часто называют километровой.

Расстояния между километровыми линиями на картах разных масштабов различны и указаны в таблицах в справочной литературе (см. табл). На карте масштаба 1:500000 наносятся лишь выходы линий километровой сетки на внутренней рамке каждого листа через 2 см (10 км на местности).

Километровая сетка на карте используется при определении прямоугольных координат и нанесении на карту объектов по их координатам, измерении на карте дирекционных (основных, главных) углов, при докладах, постановке задач, составлении сообщений и т.п.

Все линии километровой сетки на карте подписывают цифрами, причем линии, ближайшие к углам рамки, подписывают полным числом километров, другие – сокращенно – только последними двумя цифрами (десятки и единицы километров). При этом полные подписи возле вертикальных линий обозначают номер зоны (одна или две первых цифры и расстояние в километрах (всегда три цифры) от начала координат.

При определении полных координат объекта по оцифровке километровой линии, которая образует южную сторону квадрата, в котором расположен объект, находят и записывают полное значение абсциссы Х в километрах. Потом измеряют расстояние от объекта к этой километровой линии в метрах и прибавляют его к абсциссе.

После этого определяют значения ординаты объекта, для чего находят по северной или южной стороне рамки карты значения ординаты вертикальной километровой линии, которая образует западную сторону квадрата, в котором находится объект. К полученному значению прибавляют расстояние в метрах, измеренное от точки к западной координатной линии.

Рассмотрим на примере рис. 5.

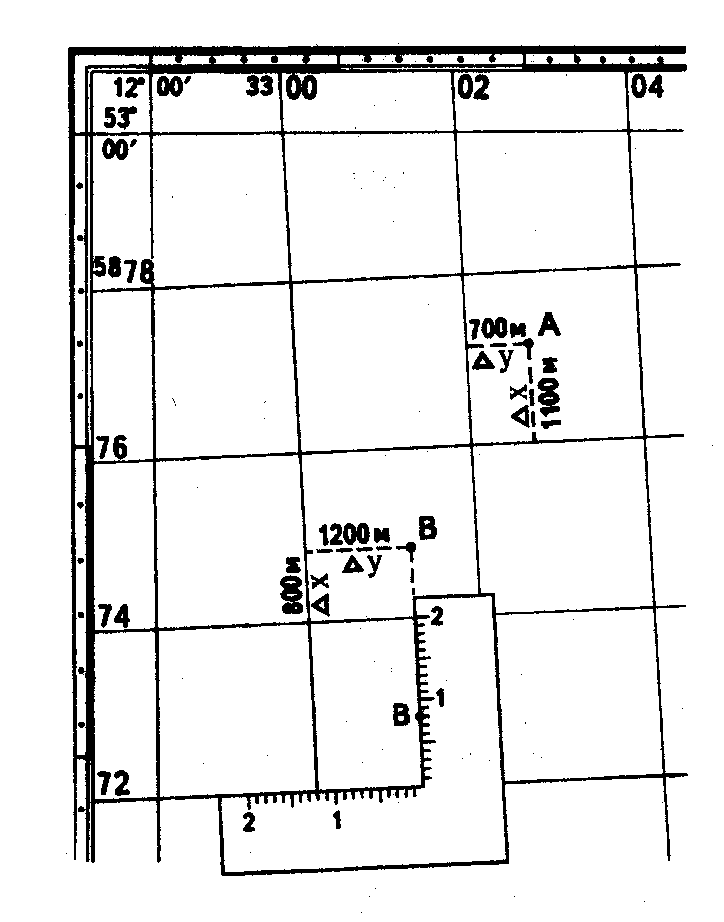
Итак, координаты точки внутри клетки километровой сетки определяют по координатам ближайших к точке линий сетки. Их читают прямо с карты – они подписаны в километрах. Далее измеряют оставшееся расстояние от линии до точки (по вертикали – Х, по горизонтали – Y). Эти величины называются приращениями координат и измеряются по перпендикуляру от ближайшей линии километровой сетки до точки. Пользуясь масштабом карты, переводят измеренный отрезок в метры и прибавляют его к значениям Х и Y. Окончательные значения координат точки равны:

Х_А = Х_{ю. линии километровой сетки} + ∆х (приращение)

Y_А = Y_{з. линии километровой сетки} + ∆y (приращение)

Итак, координаты точки А: Х_А=5877,1 км, Y_А=3302,7 км. Т.е. точка А находится к северу от экватора на 5877,1 км, 3-й зоне, к западу от осевого меридиана этой зоны на 197,3 км (500 км – 302,7 км). Площадь квадрата километровой сетки равна 1 км². Большие по площади объекты (озеро, город,…) занимают на карте несколько квадратов и их частей. Это позволяет сразу приблизительно оценить по карте площадь объекта.

При работе на ограниченной территории, изображенной, например, на одном листе карты, используют сокращенные координаты, то есть указывают только десятки и единицы километров, сотни, десятки и единицы метров.

Точность определения координат зависит от масштаба карты и не превышает 0,2 мм в масштабе карты.

В границах одной координатной зоны километровые линии соседних листов карты строго совпадают и образуют единую километровую сетку. На стыке соседних зон километровые линии располагаются под некоторым углом друг к другу (рис.2.13), так как осевые меридианы сопредельных зон не параллельны между собой. Если, например, определить координаты точки В по координатной сетке сопредельного листа, расположенного в другой зоне, то по этим координатам невозможно вычислить расстояние между указанными точками, так как начало координат в каждой зоне разное. Поэтому на листах топографических карт, расположенных в пределах 2⁰ к востоку и западу от крайнего меридиана зоны, наносят дополнительную координатную сетку соседней зоны. Ее координатные линии подписывают за внешними рамками листов карты.

При необходимости вычисляют прямоугольные координаты точек по известным геодезическим координатам и, наоборот, используют следующие приближенные формулы:

Широта ;

Долгота ,

где φ, λ – геодезические широта и долгота точки в градусах;

N – номер зоны;

X, Y – прямоугольные координаты точки в километрах;

111,2 - средняя длина в километрах дуги меридиана в 1⁰.

В инженерной практике нередко используют произвольную систему прямоугольных координат, которую еще называют условной. Начало этих координат выбирают произвольно, а ось абсцисс ориентируют по направлению магнитного меридиана, проходящего через начало координат.