1.2 Определение допускаемых напряжений изгиба.

Определение коэффициента долговечности:

K_FL=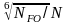 , (8)

где N_FO-число циклов перемены напряжений , N_FO=4∙10⁶ циклов [2,с.56],

Определение допускаемых напряжений изгиба

Для шестерни:

[]_FO1=370 Н/мм² [2,с.52] .

Для колеса:

[]_FO2=1,03∙НВ, (9)

Определение допускаемых напряжений изгиба

Для шестерни:

[]_F1=K_FL1∙[]_FO1, (10)

Для колеса:

[]_F2=K_FL2∙[]_FO2 (11)

Дальнейший расчет будем выполнять по наименьшему значению []_F

Таблица 1 – Механические характеристики материалов зубчатой передачи

Элемент передачи	Марка стали	Термообработка	Твердость	[]H, Н/мм2	[]F, Н/мм2
Шестерня
Колесо

1.3 Проектный расчет зубчатой передачи

Межосевое расстояние а_w, мм, определим из условия контактной выносливости активной поверхности зубьев по формуле [2, с.61]:

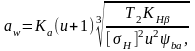(12 )

где K_а = 43 – расчетный коэффициент для косозубых колес;

u –передаточное число;

T₂ - момент на тихоходном валу;

К_Нb - предварительно принятое значение коэффициента нагрузки;

y_ba = 0,4 - коэффициент ширины венца по межосевому расстоянию.

По ГОСТ 2185, согласно [2, с.326], принимаем ближайшее значение межосевого расстояния

Определение модуля зацепления по [2, с.62]:

m= (0,01÷0,02)а_w, (13)

Принимаем по ГОСТ 9563

Определение угла наклона зубьев:

Примем предварительно угол наклона зубьев β =10°.

Определение числа зубьев шестерни и колеса:

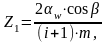(14)

Уточним значение угла наклона зубьев:

(15)

Основные размеры шестерни и колеса [2, с. 63]:

диаметры делительные:

d₁=m∙z₁/cosβ, (16)

d₂= m∙z₂/cos β

проверка:

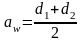(17)

диаметры вершин зубьев:

d_a1= d₁ + 2m, (18)

d_a2= d₂ + 2m,

ширина колеса: b₂= y_baa_w ,

ширина шестерни: b₁= b₂ + 4 мм

Окружная скорость колес и степень точности передачи [2,с.64]:

(19 )

где ₁– угловая скорость ведущего вала; ₁ = 41,85 рад/с.

При такой скорости для косозубых колес по [1, с.64] назначаем степень точности передачи.

Проверяем зубья по контактным напряжениям по формуле [1, с.64]:

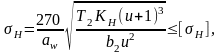(20)

где K_H - коэффициент нагрузки, определяемый по формуле [1, с.294]:

K_H=K_HbK_HaK_Hu, (21)

где K_Hb - коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца [2, с.64];

K_Ha - коэффициент, учитывающий неравномерность распределения

нагрузки между зубьями [2, с.64];

K_Hu = 1,01 - динамический коэффициент [2, с.64].

Проверяем зубья на выносливость по напряжениям изгиба.

Услов ия прочности [2, с.65]:

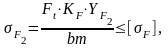(22)

где F_t - окружная сила в зацеплении, Н

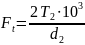
K_F - коэффициент нагрузки;

Y_F - коэффициент формы зуба;

[s_F] - допускаемые напряжения изгиба, МПа.

Коэффициент нагрузки [2, с.65]:

K_F = K_{F b} K_Fu , (23)

где K_Fb - коэффициент неравномерности нагрузки по длине зуба;

K_Fu - коэффициент динамичности.

Подставляя численные значения, имеем:

Таблица 2 – Параметры зубчатой передачи

Наименование параметра, единица измерения	Обозначение параметра и числовое значение
Угловая скорость вала, рад/с ведущего ведомого
Номинальный момент на ведомом валу, Нм
Степень точности по ГОСТ 3675-81
Число зубьев шестерни колеса
Модуль, мм
Наименование параметра, единица измерения	Обозначение параметра и числовое значение
Делительный диаметр, мм шестерни колеса
Ширина зучатого венца, мм шестерни колеса
Вид зубьев
Угол наклона зубьев β

Проверочный расчет
параметр		Допускаемое значение	Расчетное значение
Контактные напряжения, σ, Н/мм2
Напряжение изгиба,	σF2, Н/мм2

Перечень использованной литературы

1 Куклин Н.Г. Куклина Г.С. Детали машин, 1987.-383с.

2. Шейнблит А. Е. «Курсовое проектирование деталей машин», издание второе, 2004.-454с.