3. Число элементов множества

Для любого множества М число элементов (мощность множества) будем

обозначать п (М).

Пусть задано несколько множеств (подмножеств одного универсального множества W): A, B, C, … c числом элементов в каждом соответственно: п (А),

п (В), п (С), …

Решим задачу о количестве элементов в множестве, записанном в виде

формулы, т.е. состоящем из нескольких множеств, связанных операциями пересечения, объединения, дополнения.

Дано: А, В, п (А), п (В).

Определить: число элементов в объединении п (АUВ).

Решение:

Для непересекающихся множеств число элементов объединения равно сумме элементов в каждом из объединяемых множеств:

п (АUB) = п (А) + п (В).

Общий случай (два множества имеют общие элементы):

п (АUB) = п (А) + п (В) – п (А∩B)

Общий случай (три множества имеют общую часть):

n (АUBUC) = n (A) + n (B) + n (C) – n (A∩B) – n (A∩C) – n (C∩B) +

+ n (A∩B∩C).

Лекция № 3

Тема: Отношения

Цель: Ознакомить с понятием отношений, свойствами бинарных отношений и операциями над бинарными отношениями

План

1. Отношения.

2. Свойства бинарных отношений.

   0. Рефлексивность.

   1. Симметричность.(Самостоятельное изучение).

   2. Транзитивность.

3. Операции с бинарными отношениями.(Самостоятельное изучение).

1. Отношения

Говорят, что элементы вектора (а₁,а₂,а₃,…а_п ) находятся в отношении R, если

этот вектор принадлежит множеству R. Подмножество R  М^п называется п – местным (п –арным) отношением на несущем множестве М. Множество М является несущим для отношений любой арности, которые на нем построены. Такие отношения так же называют признаками.

Для п = 1 отношение называется унарным (по сути свойства одноместных отно-

шений – это свойство подмножеств М, термин отношение употребляют редко);

для п = 2 – бинарным ( т.е. отношением между двумя элементами множества М).

Примером трехместного (тернарного) отношения является множество троек на-

падающих в хоккейной команде. Каждый из нападающих находится в этом отношении со всеми игроками своей тройки (каждый нападающий может участвовать более чем в одной тройке).

Отношение – то же множество, элементами которого являются векторы размер-

ности п или, при другой записи, цепочки длины п, составленные в алфавите М и отобранные в соответствии с отношением R.

Пример1:На множестве N отношение

а) «≤» выполняется для пар (7,9), (7,7), но не выполняется для пары (9,7);

б) «иметь общий делитель, отличный от единицы выполняется для пар (6,9), (4,2), (2,4), (4,4), но не выполняется для пар (7,9), (9,7)

Пример2: Построить бинарное отношение R, которое определяется словами так: «в латинском алфавите символ встречается раньше» на несущем множестве

М = {a,b,c,d}.

Решение

Примерами элементов отношения R могут быть векторы (а,с),(с,d)… или цепочки ас, сd,bd…, такие, в которых на первом месте стоит буква, встречающаяся в латинском алфавите раньше по сравнению с буквой, стоящей на втором месте.

Отношение R является подмножеством множества М²:

М² = {aa,ab,ac,...,dd}, из которого элементы отбираются в соответствии со следующей процедурой R = {xy |x"меньше"y}.

R = {ab, ac, ad, bc, bd, cd}.

Отношения любой арности можно задать одним из способов задания множеств (перечислением элементов, порождающей процедурой, характеристическими признаками). Кроме того, бинарные отношения можно задавать:

• С помощью матрицы смежности – квадратной матрицы, столбцы и строки которой обозначены элементами несущего множества, а элементы имеют следующее значение

1, если а Ra_ј

С_{ij =}

0, в противном случае.

С	a	b	c	d
a	0	1	1	1
b	0	0	1	1
c	0	0	1	1
d	0	0	0	1

Пример 3:

Построить матрицу смежности для конечного множества {1,2,3,4,5,6}из примера 1.

а) б)

						1			2			3			4			5			6
			1			1			1			1			1			1			1
			2			0			1			1			1			1			1
			3			0			0			1			1			1			1
			4			0			0			0			1			1			1
			5			0			0			0			0			1			1
			6			0			0			0			0			0			1

	1	2	3	4	5	6
1	0	0	0	0	0	0
2	0	1	0	1	0	1
3	0	0	1	0	0	1
4	0	1	0	1	0	1
5	0	0	0	0	1	0
6	0	1	1	1	0	1

• С помощью ориентированного графа – элементы несущего множества М изображаются на плоскости в виде вершин графа (точки с обозначением рядом элементов несущего множества), а затем вершины, пары которых входят в множество R, соединяются с помощью стрелок (дуг). Начинается стрелка в первом элементе пары, заканчивается - во втором, число таких стрелок равно числу элементов в множестве R.

Пример 4: Построить ориентированный граф для множества из примера 1.

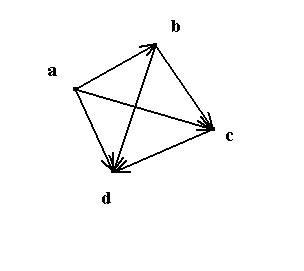
Для каждого бинарного отношения R можно построить обратное отношение R^-1 (читается: R в минус первой степени), поменяв местами в каждом элементе R проекции векторов.

R = {ab,ac,ad,bc,bd,cd}

R^-1 = {ba,ca,da,cb,db,dc}.

Отношение Q обратно отношению R тогда и только тогда, когда для каждой пары из R выполняется условие:

хRy следует yQx