Координати вектора

Теорема. Будь-який вектор на площині можна розкласти єдиним чином за базисними векторами, тобто

Коефіцієнти розкладу х і у цього вектора називаються координатами вектора в даній системі координат і записують = (х; у).

Довжина вектора .

Якщо вектор задано двома точками А(х_А;у_А), В(х_В;у_В), то координати вектора визначаються за формулою: АВ = (х_в-х_А; у_в-у_А).

Дії над векторами в координатній формі

На площині	В просторі
= (х1 ; у1); = (х2 ; у2)	= (х1 ; у1; z1); = (х2 ; у2; z2)
Сума
+ = (х1 + х2; у1 + у2)	+ = (х1 + х2; у1 + у2; z1 + z2)
Різниця
- = (х1 - х2; у1 - у2)	- = (х1 - х2; у1 - у2; z1 - z2)
Множення вектора на число
k ∙ = (k ∙ х1 ; k ∙ у1)	k ∙ = (k ∙ х1 ; k ∙ у1; k ∙ z1)
Кут між векторами
Відстань між двома точками

Означення. Скалярним добутком двох векторів = (х₁; у₁; z₁) та = (х₂; у₂; z₂) називається число .

Теорема. Скалярний добуток векторів дорівнює добутку їх абсолютних величин на косинус кута між ними.

З цієї теореми випливає, що якщо вектори перпендикулярні, то їх скалярний добуток дорівнює нулю. І навпаки, якщо скалярний добуток відмінних від нуля векторів дорівнює нулю, то вектори перпендикулярні.

Властивості скалярного добутку:

1. ;

2. ;

3. ;

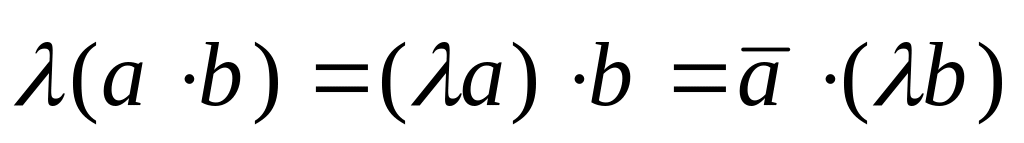4. Якщо , то ; якщо , то .

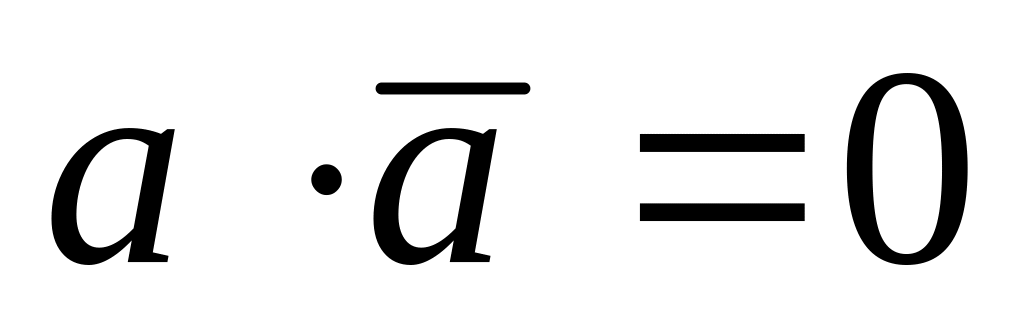Виходячи з формул скалярного добутку векторів, кут між векторами можна обчислити наступним чином:

Приклад. Знайти модуль вектора 4 - 3 , якщо = (2; -3), =(-4; 1).

Розв’язання

Знайдемо координати векторів 4 і 3 :

4 = (8; -12); 3 =(-12; 3)

Знайдемо координати різниці векторів 4 - 3 :

4 - 3 = (8 - (-12); -12 - 3) = (20; -15)

Знайдемо абсолютну величну вектора 4 - 3 :

Відповідь. 4 - 3 =25.

Приклад. При якому значенні m вектори = (m; -4) і = (-2; 3) перпендикулярні.

Розв’язання

Вектори перпендикулярні, якщо їх скалярний добуток дорівнює нулю:

x₁x₂ + y₁y₂ = 0

Підставимо координати векторів і

-2m + (-4) ∙ 3 = 0;

-2m - 12 = 0;

-2m = 12;

m = - 6.

Отже, вектори і перпендикулярні при m = - 6.

Відповідь. m = - 6.

Приклад. Дано точки B (-1; 3); С(8; -12).Знайти координати точок М і N, які ділять відрізок на три рівні частини.

Розв’язання

Точка N ділить відрізок ВС у відношенні

Тоді ;

Підставимо в ці формули координати точок В і С.

Маємо: ;

Отже, N (5;7).

Точка М ділить відрізок BN навпіл, тоді: ;

Підставимо координати ; .

Отже, М(2; -2).

Відповідь. М(2; -2).

Приклад. Довести, що трикутник з вершинами А(2; 2); В(-1; 6); С(-5; 3) - прямокутний.

Доведення

Знайдемо довжини сторін трикутника ABC:

= (-1 - 2; 6 - 2); ;

= (-5 - (-1); 3 - 6) = (-4; 3); ;

= (-5 - 2; 3 - 2) = (-7; 1); .

Використаємо теорему обернену теоремі Піфагора: якщо в трикутнику сума квадратів двох сторін дорівнює квадрату більшої сторони, то цей трикутник прямокутний.

Так як АВ² + ВС² = 5² + 5² = 25 + 25 = 50 = АС², то трикутник ABC -прямокутний і величина кута ABC = 90°, що і треба було довести.

Відповідь. Трикутник з вершинами А(2; 2); В(-1; 6); С(-5; 3) - прямокутний.

Приклад. Знайти на вісі Оу точку М, яка знаходиться на відстані 5 одиниць від точки К(3;7).