6. Разрешающие уравнения теории упругости

В сводке основных уравнений теории упругости – статических (5.2), совместимости деформаций (5.8), (5.9) и физических (5.15), (5.16) присутствуют 15 неизвестных функций координат x, y, z: функции напряжений , функций деформаций и функций перемещений u, v, w, а также постоянные E, G и , причем для изотропного материала . Путем соответствующих математических преобразований в уравнениях (5.2), (5.8), (5.15) и (5.16) можно сократить число искомых функций и получить разрешающие уравнения в напряжениях или перемещениях.

Разрешающие уравнения в напряжения

Бельтрами – Митчелла

Пользуясь уравнениями закона Гука (5.15) в уравнениях совместимости деформаций (5.8) и (5.9) выразим через , т.е. .

Отпуская довольно громоздкие выкладки, приведем окончательные формулы

(6.1)

Здесь принято:

Символ - символ оператора Лапласа для функции он имеет вид

Как частный случай отметим, если массовые силы X, Y, Z не зависят от координат x, y, z, т.е. они постоянные по объему тела, то и соответствующие производные обращаются в нуль. Тогда уравнение (6.1) упрощаются и принимают вид:

(6.2)

Выражение (6.1) и (6.2) - уравнения Бельтрами – Мичелла, разрешающие уравнения теории упругости в напряжениях. Дополнив к ним статические уравнения равновесия (5.2), получаем систему девяти уравнений. Учитывая закон парности касательных напряжений (5.3), согласно которому

мы приходим к системе шести уравнений, включающую искомые функции

Разрешающие уравнения в перемещениях Ляме

Пользуясь уравнениями закона Гука в виде (5.16) в уравнениях равновесия (5.2) выразим через , а с помощью соотношений Коши (5.7) переходим от перемещениям u, v, w.

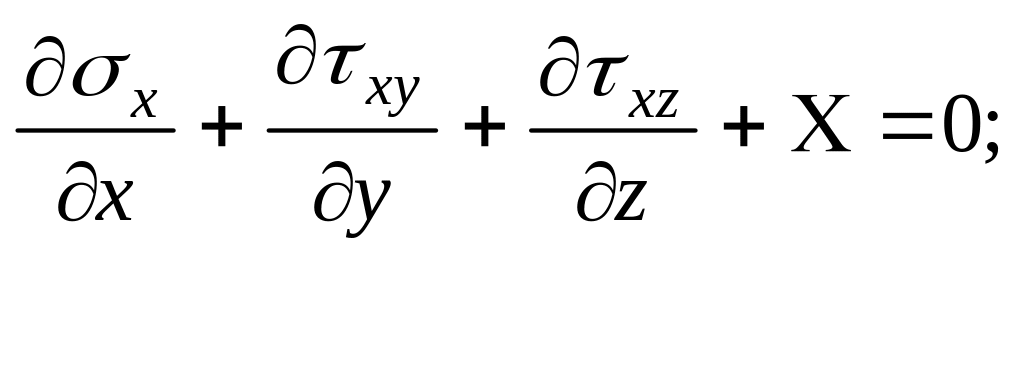
где

G= , далее получим

Сократим на G и на основании соотношений Коши

получим

Оператор Лапласа

Окончательно

Применяя принцип циклической перестановки, получим

(6.3)

где -объемная деформация

Полученные выражения (6.3) – разрешающие уравнения теории упругости в перемещениях, формулы Ляме. С помощью уравнений Ляме (6.3) удобнее и проще решать задачи с кинетамитечскими граничными условиями (задача II рода)

7. Плоская задача теории упругости

Плоская задача теории упругости делится на два вида: плоское (двухосное) напряженное состояние и плоская деформация.:

Плоское напряженное состояние возникает в пластине от нагрузки, приложенной по ее контуру или объёму и остающейся по толщине пластины постоянной или изменяющейся симметрично относительно серединной плоскости пластины, т.е. от нагрузки, действующей в плоскости пластины. Примерами простейшего плоского напряженного состояния для прямоугольных пластин являются равномерное растяжение, чистый плоский изгиб, чистый сдвиг.

Плоская деформация имеет место, если выполнены следующие условия:

а) из трех компонентов вектора перемещения u, , переменными во всех точках пластины являются два компонента в одной плоскости, а третий либо равен нулю, либо сохраняет отличие от нуля, по постоянное значение. Таким компонентам при плоской деформации в плоскости ху является ;

б) если компоненты перемещений u, является функциями только двух переменных х, у, т. е. задача для плоской деформации пластины двухмерная.

Сводка основных уравнений теории упругости для плоской задачи.

Тензор напряжений: (7.1)

Тензор деформаций: (7.2)

Статические уравнение равновесия (Навье)

(7.3)

Условия равновесия граничного элемента (статические граничные условия)

(7.4)

Геометрические уравнения (Коши)

(7.5)

Уравнения совместности деформаций (Сен-Венана)

(7.6)

Физические уравнения (закон Гука)

прямая форма

(7.7)

обратная форме

(7.8)

Уравнения физического закона для плоского напряженного состояния и плоской деформации по форме совпадают при замене Е на Е₁ и на

(7.9)

Разрешающие уравнения в напряжениях (Леви)

При условии, что массовые силы постоянные по объему (схема вывода прежняя)

(7.10)

К этому уравнению необходимо дополнить статические уравнения равновесия (7.3) и получить систему трех уравнений с тремя неизвестными Как следует из выражения (7.10), - функция гармоническая.

Разрешающие уравнения в перемещениях

(схема вывода прежняя)

(7.11)

где

Решение плоской задачи с помощью

функции напряжений Эйри

Решение плоской задачи можно существенно упростить, если перейти от трех неизвестных функций к одной функции , называемой функцией напряжений (функцией Эйри). Полагаем, что массовые силы постоянны по объему , . Предположим, что существует такая функция , через которую можно выразить искомые функции по следующей схеме

(7.12)

Легко проверить, что уравнение равновесия (7.3) выполняются при любой функции , соответствующей условиям (7.12)

Таким образом любая функция соответствует равновесным полям напряжений (7.12), т.е. удовлетворяет условиям равновесия (это отметил английский ученый Джордж Эйри в 1862 г., отсюда – функцию напряжений называют функцией Эйри).

Из всех равновесных полей напряжений истинное (действительное) поле должно еще к тому же удовлетворить условно сплошности деформаций (7.6) согласно зависимости (7.10) запишем

(7.13)

Подставив функцию , согласно (7.12), в выражение (7.13), получим

т.е. получим (7.14)

или раскрыв двойной оператор (7.14), получим

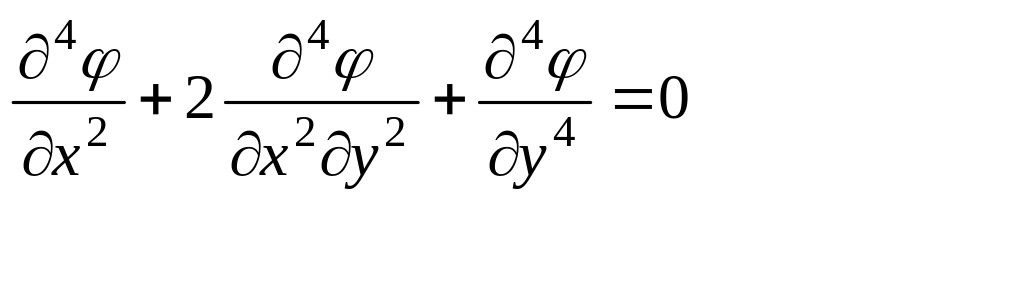
(7.15)

Уравнение (7.5), называют гармоническим уравнением плоской задачи.

В заключении отметим, что практическое решение отдельных задач с помощью функции напряжений заключается в следующем: интуитивно задаются некоторым выражением для функции напряжений в виде многочлена второй или третьей степени вида

(7.16)

Затем составляются выражения для напряжений и , согласно зависимостям (7.12), и подбирают неизвестные коэффициенты С₁, С₂, С₃, С₄ такими, чтобы удовлетворялись статические граничные условия решаемой задачи.

Список рекомендованной литературы.

1. Л.П. Винокуров. Теория упругости и пластичности.

Изд. ХГУ. Харьков 1965 – с. 327

2. А.В. Александров, В.Д. Потапов. Основы теории упругости и пластичности: Учеб. для строит. спец. вузов. – М.: Высш. шк, 1990 – 400с.

3. А.П. Филин. Прикладная механика твердого деформируемого тела. Изд. Наука, Москва, 1975 г. т. 1 – с. 832