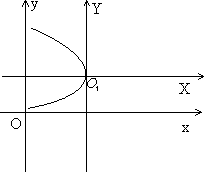
4. Парабола

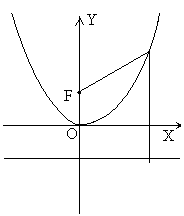
Параболой называется множество точек плоскости, одинаково удаленных от заданной прямой (директрисы) и заданной точки (фокуса)

П усть точка F( , 0) – фокус. Прямая BD – директриса параболы ;

М(х,у) – произвольная точка параболы, FD = Р >0 параметр параболы.

По определению параболы МF = МВ. Уравнение параболы с вершиной в точке 0(0;0) и директрисой BD, заданной уравнением х = , имеет канонический вид:

1. у² = 2 ρх .

Замечание: если положить х = , то y= p, то есть NF=p (NF OX). Эксцентриситет параболы  = 1.

Другие виды параболы:

2. у ² = - 2 ρх - парабола с осью симметрии OХ, фокусом F(- , 0) и директрисой x= .

3. х

   X

   

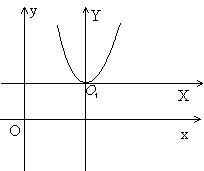
   ² = 2 ρу- парабола с осью симметрии OY, фокусом F(0, ) и директрисой y= - .

4. х² = -2 ρу- парабола с осью симметрии OY, фокусом F(0,- ) и директрисой y= .

Преобразования координат.

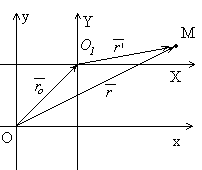
1.Параллельный перенос.

Изменяется начало координат, а направление осей и масштаб остаются неизменны.

, ^’{X,Y}, {x, y}, = ₁+ ₀, тогда

или

- формулы преобразования координат при параллельном переносе осей координат

2.Поворот осей координат .

П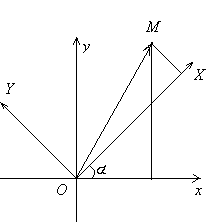 усть М(х;у) в системе xoy, M(X,Y) в системе XOY.

Тогда формулы перехода при повороте осей координат на угол 

к системе хоу имеют вид:

,

а к системе XOY: .

Кривые 2-го порядка с осями симметрии, параллельными осям координат.

1.Эллипс.

У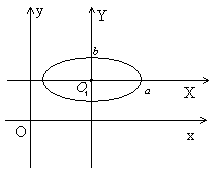 равнение эллипса в системе XOY: .

Уравнение эллипса со смещенным в точку О₁(m,n) центром:

.

Возможны случаи вырождения эллипса в точку, например,

- точка O₁ (m,n), или мнимый эллипс: .

2.Гипербала.

У равнение гиперболы с центром в точке О₁(m,n): , (1).

Уравнение гиперболы, вырожденной в свои асимптоты ,

имеет вид: .

Уравнение гиперболы, сопряженной к данной: , (2).

3. Парабола.

Парабола с вершиной в точке О1(m,n), с осью симметрии параллельной ОХ, р>0.

Парабола с вершиной в точке О1(m,n), с осью симметрии параллельной ОХ.

Парабола с вершиной в точке О1(m,n), с осью симметрии параллельной ОY.

Парабола с вершиной в точке О1(m,n), с осью симметрии параллельной ОY.

Если сравнить уравнения кривых 2-го порядка с осями симметрии, параллельными осям координат с общим уравнением кривой второго порядка, то очевидно, всюду коэффициент с произведением координат отсутствует, т.е. а₁₂ = 0 и

1. если кривая эллиптического типа, то а₁₁ а₂₂ >0

2. если кривая гиперболического типа, то а₁₁ а₂₂ <0

3. если кривая параболического типа (парабола или ее вырождения в пару параллельных прямых или пару слившихся прямых), то выполняется условие а₁₁ а₂₂ = 0.

Полярная система координат.

При решении многих задач аналитической геометрии оказывается более удобным определять положение точки на плоскости не прямоугольными декартовыми координатами, а так называемыми полярными координатами.

Система полярных координат задается полюсом - точкой О и полупрямой, исходящей из полюса («луч»- - полярная ось).

ОМ = ρ, МОρ =. Числа ρ и  определяют положение точки М относительно системы координат, их называют полярными координатами точки М(ρ;).

Чтобы установить взаимнооднозначное соответствие между точками плоскости и координатами этой точки, ограничим изменение полярного угла промежутком -< (или иным промежутком длины 2π). Значения , удовлетворяющие этому условию, называют главными значениями. Назовем полярные координаты ρ,  основными, если ρ ≥0, а  есть главное значение полярного угла, т.е. если -< .