11. Делимость.

Вопрос о делимости натуральных чисел, то есть вопрос о том, делится ли данное натуральное число на какие-либо другие натуральные числа, является важным для математической теории и практики. Недаром издревле широко известен факт, связанный именно с делимостью. Он состоит в том, что все натуральные числа распадаются на два множества: множество чётных чисел (то есть чисел, которые делятся на два) и множество нечётных чисел (то есть чисел, которые не делятся на два).

Если натуральное число n делится на число m, то говорят, что число n кратно числу m. Числа кратные числу m образуют арифметическую прогрессию, разность и первый член которой равны m. Общий член этой прогрессии а_k равен k∙m. Ясно, что в этой прогрессии простым числом может быть только первый член, равный m, так как остальные её члены неравны m и делятся на m.

На этом обстоятельстве основан известный в древней Греции метод построения последовательности простых чисел, называемый решетом Эрастосфена. Сначала выписывают все натуральные числа, начиная с двойки (единицу по традиции не принято считать простым числом). Затем вычёркивают из последовательности все чётные числа кроме двойки. Двойка становится первым простым числом. За ней следует тройка – второе простое число. Остальные числа, кратные трём, следует вычеркнуть (если они ещё не вычеркнуты). Третьим простым числом становится пятёрка, а числа, кратные пяти, удаляются из последовательности. Этот процесс позволяет выявить все простые числа.

2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
↑	↑		↑		↑				↑		↑				↑		↑				↑

Иногда для решения вопроса о кратности одного числа другому нет необходимости выполнять деление. Для чисел, записанных в десятичной позиционной системе счисления, используются так называемые признаки делимости. Они основаны на следующем факте, связанном с законом дистрибутивности.

Прежде всего, следует вспомнить определение делимости: если для некоторого натурального числа с выполняется равенство а = b∙с, то говорят, что натуральное число а делится на натуральное число b. Пусть число а делится на b (то есть для некоторого с₁ выполняется равенство а = b∙с₁) и, кроме того, верно равенство а = b·с₂ + d, где d ≥ 0 (легко понять, что с₁ больше или равно с₂), тогда число d должно делиться на b. Действительно, поскольку а = b∙с₁ = b·с₂ + d, получаем, что d = b∙с₁ – b·с₂ = b∙(с₁ – с₂). Таким образом, либо d = 0 (если с₁ = с₂), либо d делится на b.

Для получения признаков делимости на 10, 2 и 5 применяются сходные рассуждения. Пусть задано число а = а_n·10ⁿ + а_{n – 1}·10^{n – 1} + … + а₁·10 + а₀, тогда

1) а = 10·(а_n·10^n–1 + а_{n – 1}·10^{n – 2} + … + а₁) + а₀, и для того, чтобы а делилось на 10, на десять должно делиться число а₀, которое меньше 10. Это возможно лишь при условии а₀ = 0. Признак делимости на 10: число делится на 10, если последняя цифра десятичной записи числа а является нулём.

2) а = 2·(5·а_n·10^n–1 + 5·а_{n – 1}·10^{n – 2} + … + 5·а₁) + а₀. Признак делимости на 2: число делится на 2, если последняя цифра задаёт чётное число (0, 2, 4, 6, 8).

3) а = 5·(2·а_n·10^n–1 + 2·а_{n – 1}·10^{n – 2} + … + 2·а₁) + а₀. Признак делимости на 5: число делится на 5, если последняя цифра задаёт число, кратное 5 (0, 5).

Аналогично может быть получен и признак делимости на 4, однако, он более тяжеловесен, поскольку десять не делится на 4. Поскольку на 4 делится 100, имеем а = 100·(а_n·10^n–2 + а_{n – 1}·10^{n – 3} + … + а₂) + а₁·10 + а₀. Признак делимости на 4: число делится на 4, если число, задаваемое двумя последними цифрами, кратно 4.

Для получения признаков делимости на 3 и на 9 используются более сложные преобразования, касающиеся каждого слагаемого в десятичной записи и основанные на том, что 10ⁿ – 1 = 9·10^n–1 + 9·10^{n – 2} + … + 9 или 10ⁿ = 9·(10^n–1 + 10^{n – 2} + … + 1) + 1 = 9. Таким образом, а_n·10ⁿ = 9·а_n·с_n + а_n, где с_n = 10^n–1 + 10^{n – 2} + … + 1.

Пусть задано число а = а_n·10ⁿ + а_n–1·10^{n – 1} + … + а₁·10 + а₀, тогда число а может быть преобразовано к виду а = 9·с + (а_n+ а_n–1+ …+ а₁+ а₀). В результате получаются сходные признаки делимости на 3 и на 9: число делится на 3 (соответственно на 9), если на 3 (соответственно на 9) делится сумма цифр этого числа.

Одним из способов выявления структуры натуральных чисел является их разложение на множители. В частности при этом может быть выявлен тот факт, что число является простым. Разложение числа n на множители производится по следующей схеме. Выписываются все простые числа, не превосходящие n. Если n равно последнему простому числу в последовательности, то оно является простым числом и разложение закончено. В противном случае пытаемся разделить n на два. Если деление удалось, снова делим частное на 2. Так продолжается, пока деление на 2 не станет невозможным. Затем таким же образом делается попытка деления на 3, 5, 7 и т. д. Процесс завершается, когда очередное частное оказывается простым числом. Для примера разложим на множители число 18. Делим 18 на 2, результат равен 9. Число 9 на 2 не делится. Делим 9 на 3, результат равен 3. процесс завершён. В результате получено разложение 18 = 2·3·3 = 2·3². Интуитивно ясно, что разложение числа на простые множители проводится однозначно.

Р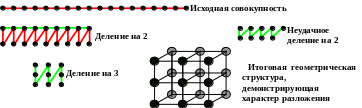 азложение на множители можно продемонстрировать физически с помощью совокупности предметов.

Чем больше сомножителей, тем многослойней структура, демонстрирующая характер разложения. Наоборот, простое число соответствует распределению всех элементов на отрезке.