6. Н Арифметика, натуральные числа. Атуральные числа и измерение отрезков.

Геометрически натуральные числа принято изображать как уходящую в бесконечность последовательность равноотстоящих друг от друга точек, расположенных на луче. Данный образ хорошо передаёт суть счёта как последовательного перечисления однородных предметов, связанного с движением во времени. Здесь наглядно проявляется тот факт, что числами (и числительными) обозначается не только количество предметов, но и их порядок при счёте.

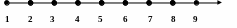
Понятие порядка является одним из важнейших в математике. Первым из натуральных чисел является единица, а каждое последующее число получается из предыдущего с помощью добавления единицы: 1, 2 = 1+ 1, 3 = 2 + 1 и т. д. Таким образом, чем больше натуральное число, тем дальше оно расположено от начала луча. Для обозначения порядка чисел и их относительной величины используются символы n < m (меньше), n ≤ m (меньше или равно), n > m (больше), n ≥ m (больше или равно), n = m (равно).

Геометрическое изображение натуральных чисел точками луча указывает на связь счёта с измерением отрезков. Фактически числовой луч превращён в линейку и позволяет измерить любой приложенный к ней отрезок и выразить его длину целым числом. Вообще же измерение отрезков является одной из самых естественных операций – речь идёт о подсчёте шагов при ходьбе.

Очень близкой к операции измерения отрезков является операция сравнения длины отрезков. Пусть, например, заданы два уже измеренных отрезка, длины которых равны n и m соответственно. Откладывая второй отрезок вдоль первого, можно установить, сколько раз он укладывается в первый и какой при этом остаётся остаток. Данная процедура даёт геометрический образ деления натуральных чисел с остатком.

Д

еление с остатком можно понимать как разбиение исходного множества из n элементов на два новых множества. Первое множество состоит из r элементов исходного множества, а второе состоит из q элементов, каждый из которых сам по себе является множеством, содержащим m элементов исходного. Если положить m равным десяти, мы придём к операции разбиения множества на десятки, что является важнейшим действием при записи чисел в десятичной системе счисления.

Простой способ деления числа n на число m с остатком таков. Из кучи, содержащей n предметов, последовательно удаляют совокупности по m предметов, считая число удалений (q), пока не останется r предметов, где r < m.

7. Равенства и простейшие уравнения.

Изначальная постановка простейших задач арифметики такова: заданы два натуральных числа и вид операции, которую нужно над ними произвести (сложить, вычесть, перемножить, разделить, возвести в степень, извлечь корень определённой степени). Однако практические вычисления с древнейших времён требуют и решения задач другого типа: заданы только одно исходное число, вид операции и полученный результат. Необходимо найти неизвестное исходное число.

Пусть, например, одно из слагаемых (таким образом, операцией является сложение) равно 7, а сумма равна 15. Каково второе слагаемое? Решение задачи должно исходить из физического смысла операций сложения и вычитания: суммирование состоит в сложении двух куч, а последующее изъятие из суммы предметов одной из исходных куч, позволяет получить вторую исходную кучу. Таким образом, вычитая из суммы известное слагаемое, можно получить искомое слагаемое.

Подобные рассуждения слишком тяжеловесны. Математическая символика позволяет кратко записывать условия простых арифметических задач и заменять рассуждения, проясняющие смысл ситуации, определёнными преобразованиями над строкой символов, выражающих задачу. Как правило, соответствующие условия записываются в виде уравнений, содержащих неизвестное число. Согласно традиции принято обозначать неизвестные числа последними буквами латинского алфавита – x, y, z, а известные числа его первыми буквами – a, b, c и т. д.

Задача, которая рассматривалась выше, записывается равенством 7 + х = 15. Смысл преобразований, необходимый для решения уравнения, таков. Если два числа равны, то при вычитании из них одного и того же числа равенство не нарушится. Следовательно, из исходного равенства 7 + х = 15 следует другое равенство: (7 + х) – 7 = 15 – 7 или х = 8. Решение получено.

В общем виде уравнение можно записать так: a + х = b. Легко получить его решение: х = b – a. Однако следует иметь в виду, что неизвестное является натуральным числом или нулём только в случае, когда b больше или равно a. Получается, что одинаковые по форме уравнения могут или иметь, или не иметь решение. В этом состоит одна из причин, по которым были введены целые числа, то есть к натуральным числам, имеющим физический смысл, были добавлены числа отрицательные.

С помощью уравнений можно описать любую арифметическую задачу, например, уравнение х² = 25 соответствует задаче извлечения корня из числа 25.

Уже в древние времена математики начали решать задачи, приводящие к так называемым неопределённым уравнениям, то есть к уравнениям, имеющим более одного неизвестного. Например, задаче: найти все натуральные слагаемые, имеющие сумму 5, соответствует неопределённое уравнение х + у = 5. Его решение таково: натуральное слагаемое х должно быть меньше суммы, то есть может принимать значения х = 1, 2, 3, 4. Неизвестное у вычисляется по формуле у = 5 – х. Решениями являются пары х=1, у=4; х=2, у=3; х=3, у=2; х=4, у=1.