Лекция №3.

Вынужденные колебания.

1. Вынужденные колебания без учёта сил сопротивления:

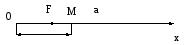
x

Проекция сил на ось OX: где – восстанавливающая сила, (н); – возмущающая сила, (н); H – амплитуда вынуждающей силы, (н); p – круговая частота вынуждающей силы, (1/с).

Получили линейное неоднородное диференциальное уравнение:

, (1.1)

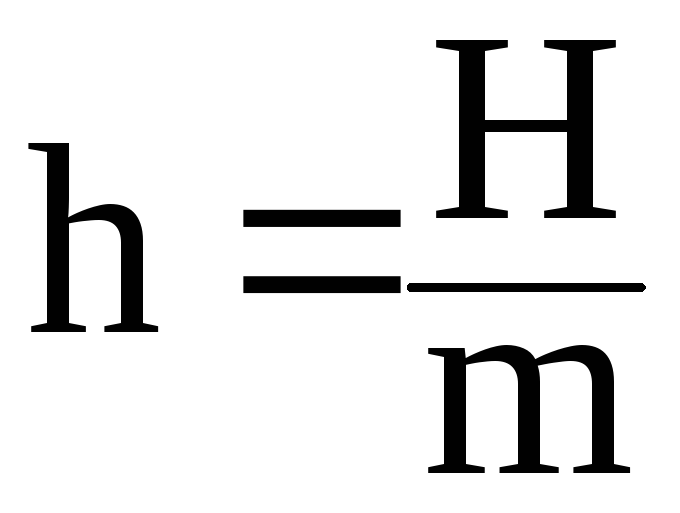где – квадрат круговой частоты свободных колебаний, (1/с); – относительная величина амплитуды вынуждающей силы(н/кг).

Общее решение уравнения (1.1) находим в виде:

, где – общее решение однородного уравнения; – частное решение.

или

Найдём и подставим в уравнение (1.1):

Из уравнения следует, что , т.е. ; , т.е. B=0.

Рассмотрим случай, когда k≠p:

B=0

В окончательном виде общее решение дифференциального уравнения (1.1) имеет вид:

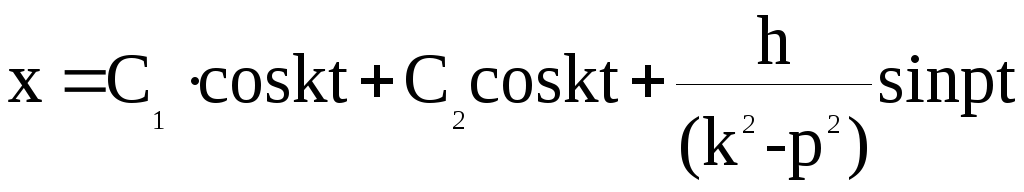(1.2)

Cи C определяются по начальным условиям, которые следует подставить в уравнение (1.2).

График амплитудно- частотной характеристики (АЧХ):

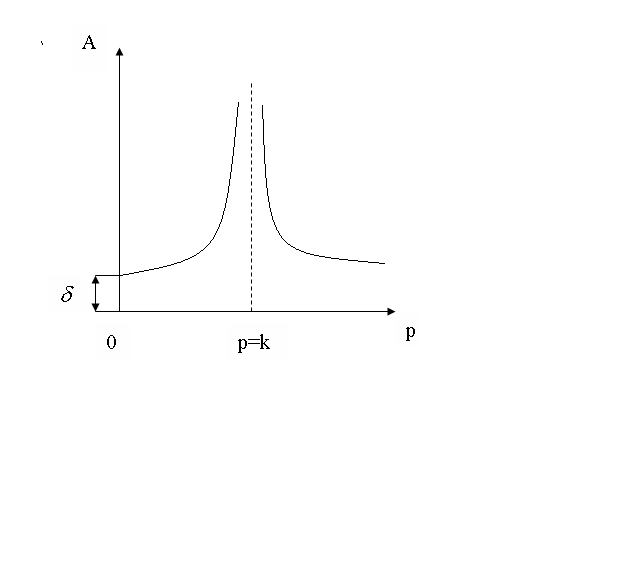
При p=0 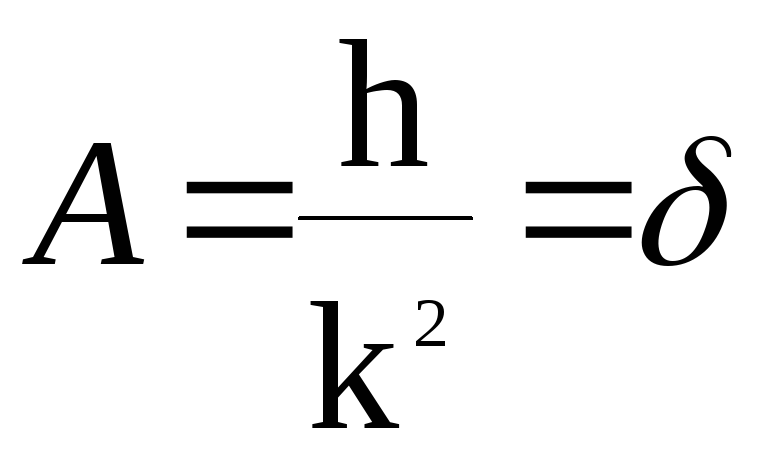, где - статическое отклонение точки под действием постоянной силы H.

Случай, когда (резонанс).

Найденное значение подставим в уравнение (1.1):

В результате сокращений получим, что , отсюда следует: , т.е. и , т.е.

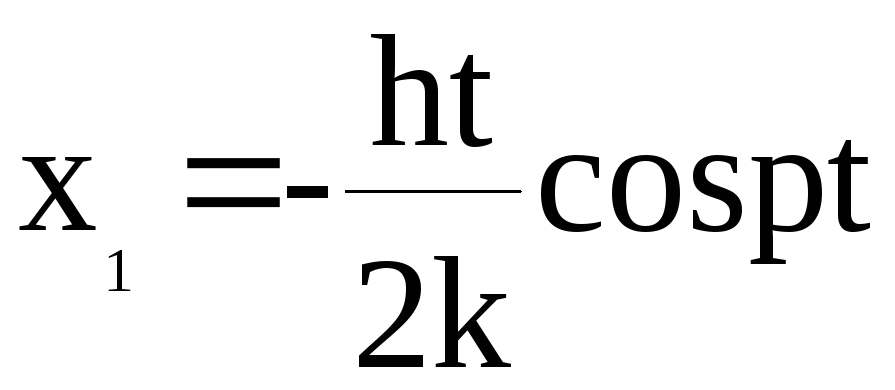
Амплитудно-частотная характеристика(АЧХ):

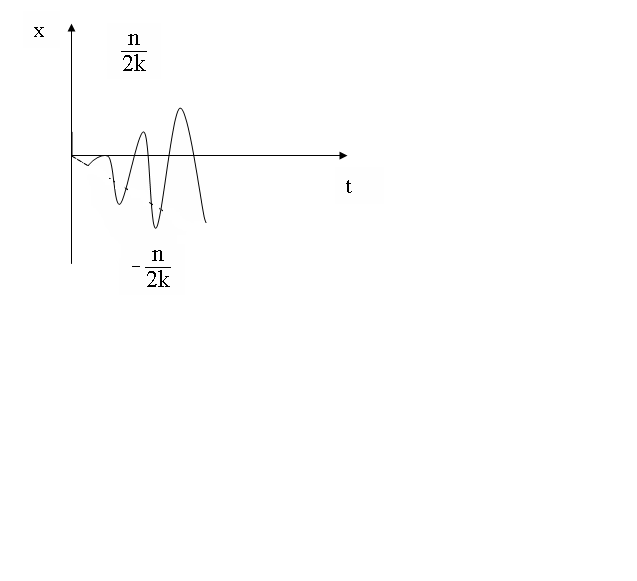
2. Вынужденные колебания с учётом сил сопротивления.

Проекция сил на ось OX: где – восстанавливающая сила, (н); – возмущающая сила, (н); H – амплитуда вынуждающей силы, (н); p – круговая частота вынуждающей силы, (1/с); – сила сопративления, (н).

Получили линейное неоднородное диференциальное уравнение:

, (2.1)

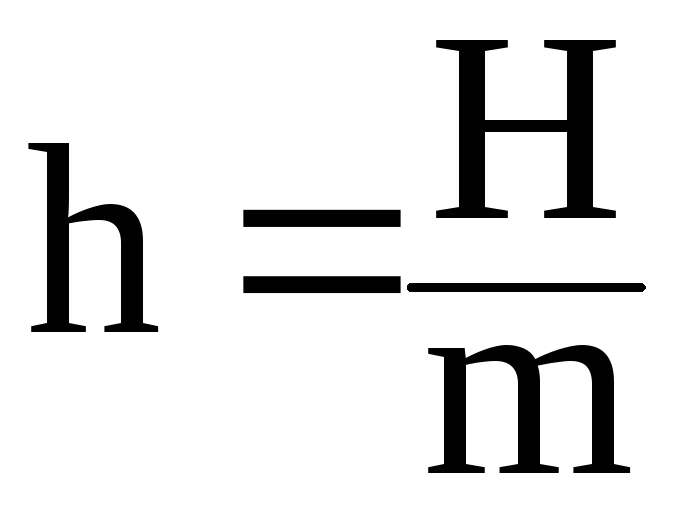где – квадрат круговой частоты свободных колебаний, (1/с); – относительная величина амплитуды вынуждающей силы(н/кг); 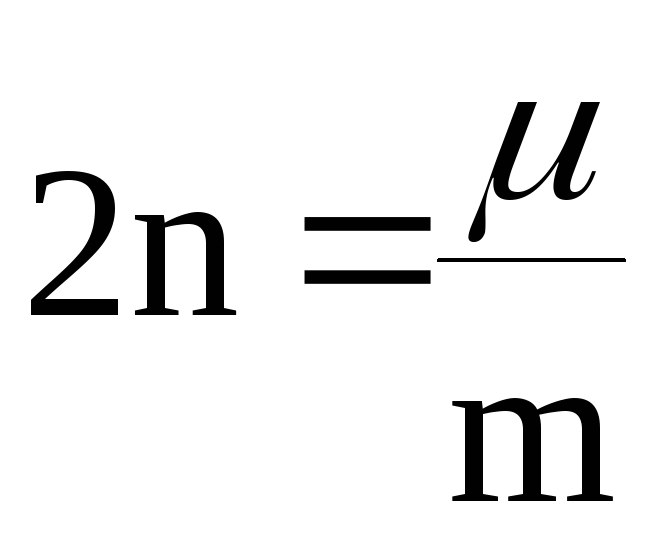, где – коэффициент затухания, (1/с).

Общее решение уравнения (2.1) находим в виде:

, где – общее решение однородного уравнения; – частное решение.

При затухающих колебаниях в случае малого сопротивления(< ):

, где – круговая частота собственных колебаний с учётом сил сопративления

В случае большого сопротивления(> ):

В случае, когда =:

После подстановки , , в (2.1) и после приравнивания коэффициентов перед синусами и косинусами в обоих частях тождества получим:

, т.е.

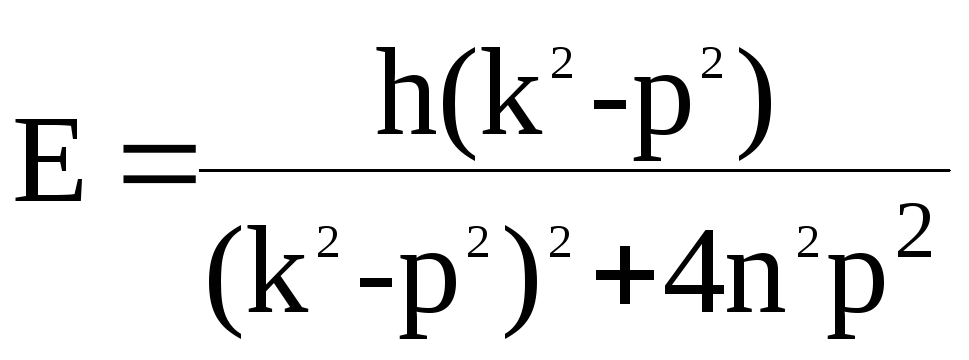
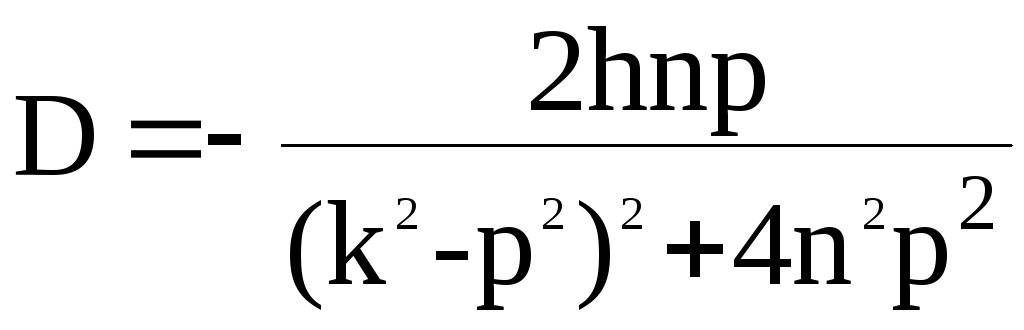
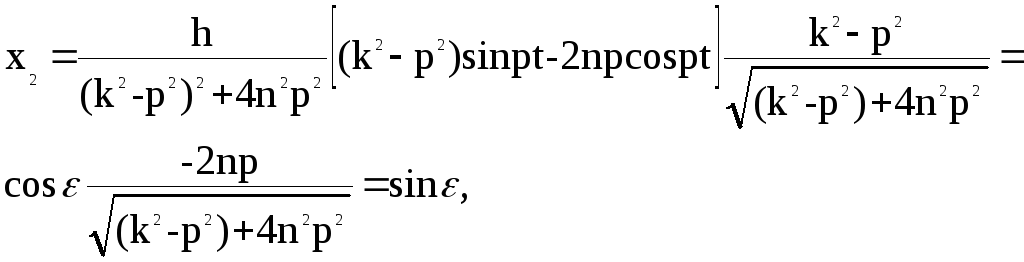
где - сдвиг фаз.

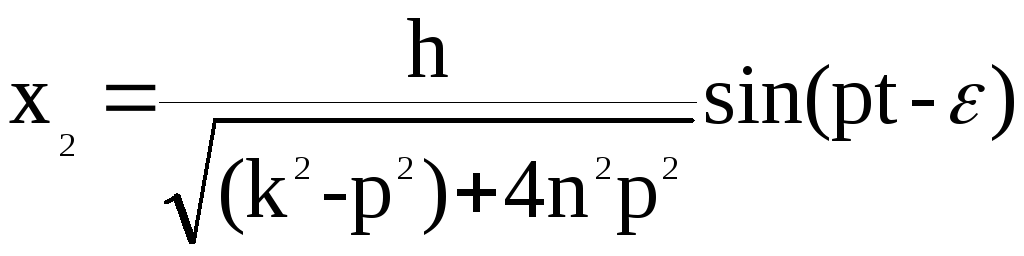
Амплитуда вынужденных колебаний равна:

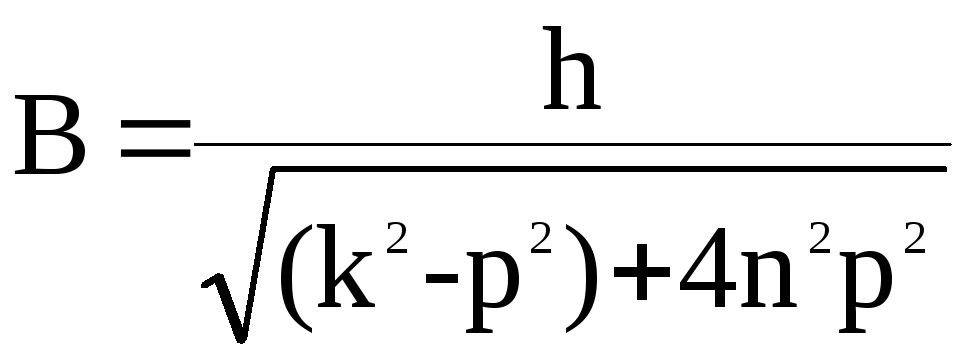(2.2)

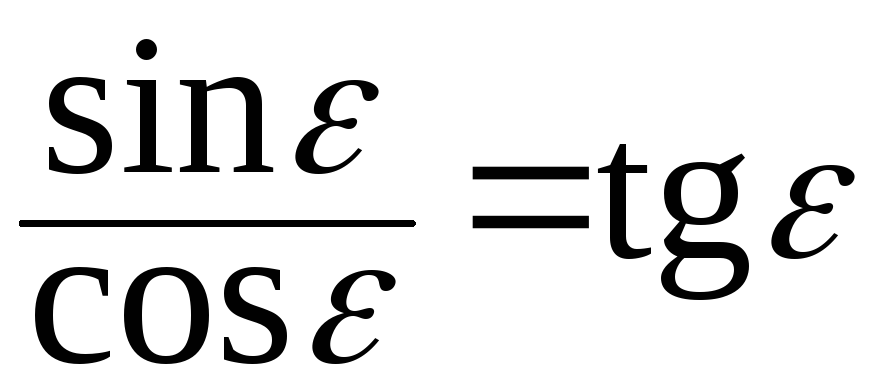, т.е.

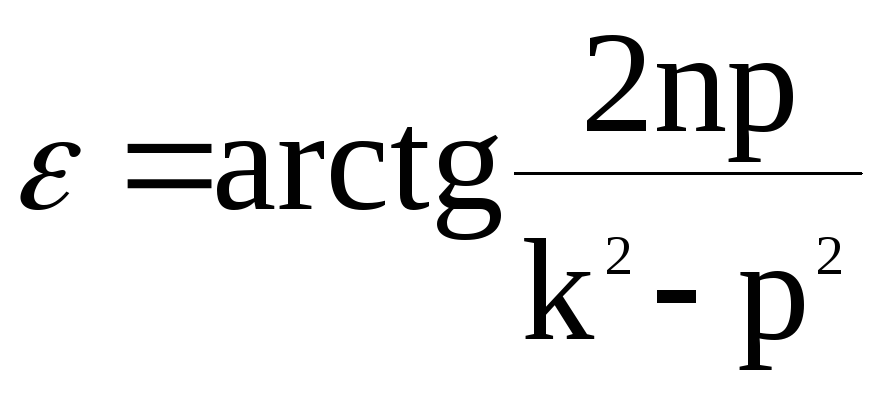
Решение уравнения (2.1) имеет вид:

, где и определяются по начальным условиям.

Разделим числитель и знаменатель выражения (2.2) на :

,

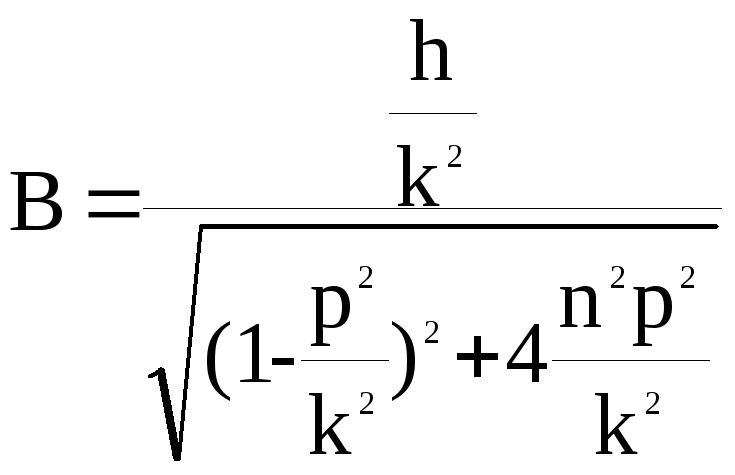где - статическое отклонение точки под действием силы H; 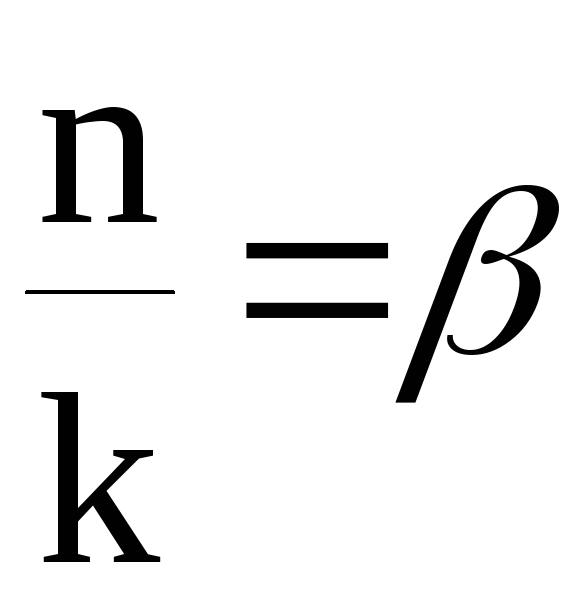- коэффициент затухания; 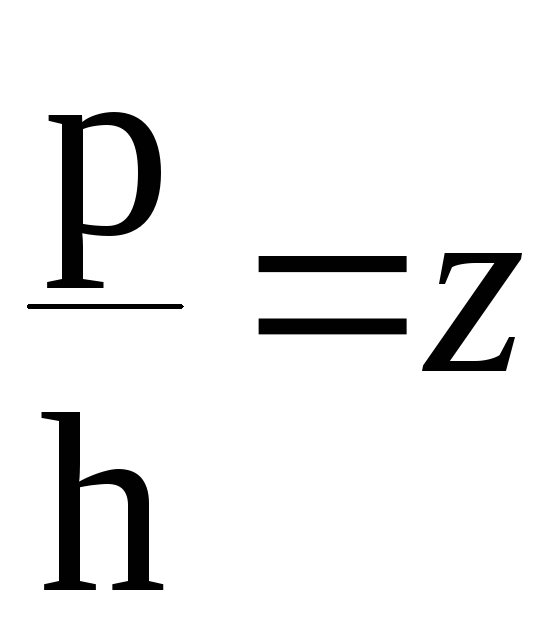- коэффициент расстройки.

B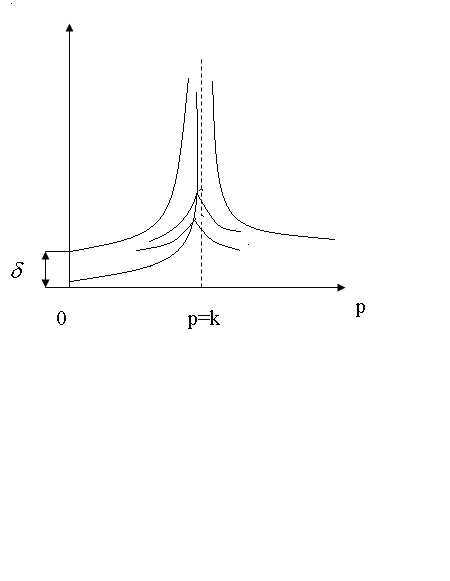

Максимумы вынужденных колебаний происходят не на резонансной частоте, когда 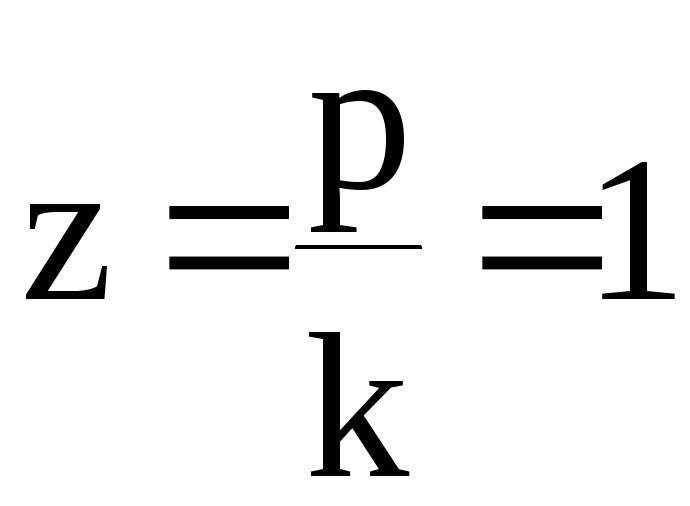, а при критическом коэффициенте расстройки: .

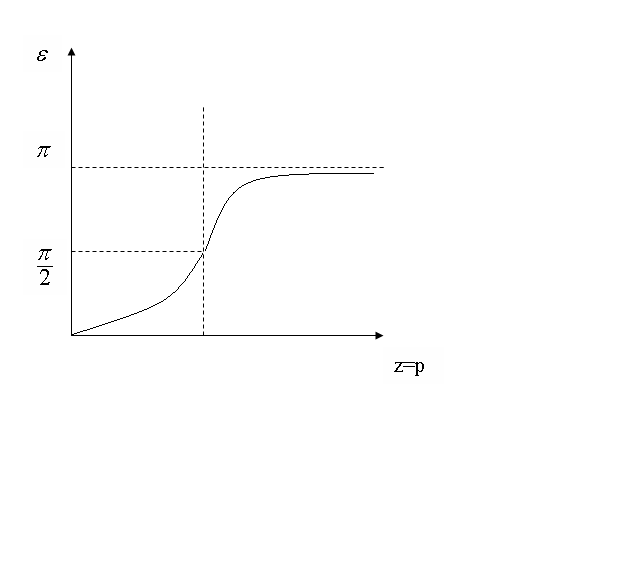
График фазо-частотных характеристик(ФЧХ):

7