Лекции по теоретической механике1 / Лекция №2

Теория колебаний

1. Свободное колебание материальной точки

2. Затухающее колебание материальной точки

1. Свободное колебание материальной точки

Свободными или гармоническими колебаниями точки называется колебательное движение под действием только восстанавливающей силы. Эта сила при движении точки всегда стремиться вернуть ее в положение равновесия. По модулю восстанавливающая сила пропорциональна расстоянию от точки до ее равновесного положения.

Т.О – положение равновесия т.М

Составим дифференциальное уравнение движения точки:

где с – коэффициент упругости (коэффициент жесткости)

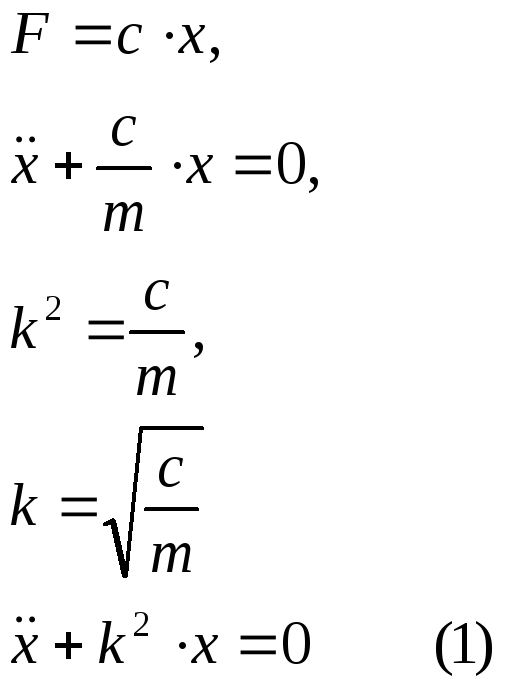
(1) – дифференциальное уравнение свободных колебаний (линейное однородное уравнение второго порядка),

где k – круговая частота свободных колебаний.

Составим характеристическое уравнение:

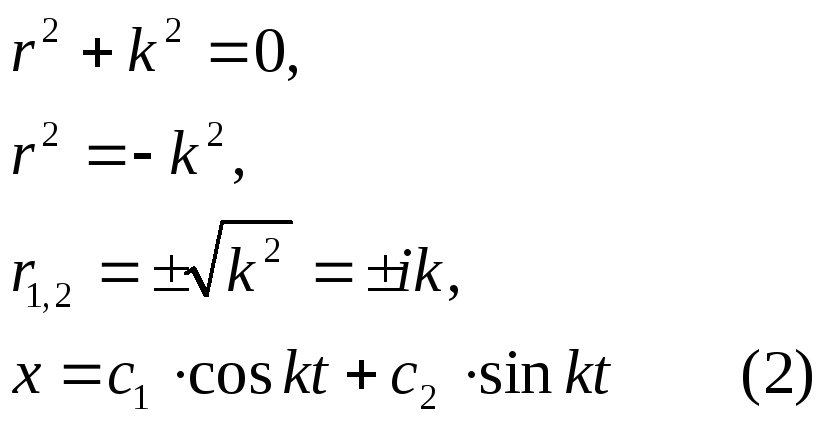
(2) - решение дифференциального уравнения.

Выразим решение дифференциального уравнения в более компактном виде:

Где a – амплитуда колебаний,

kt + α – фаза колебаний,

α – начальная фаза колебаний.

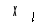
Решением дифференциального уравнения является гармонические колебания с амплитудой a и начальной фазой α.

Постоянные с1 и с2 или α и a определяются из начальных условий.

Т.к. функции синус и косинус периодические и в одинаковой фазе находятся через 2π, то определяем за период разность фаз:

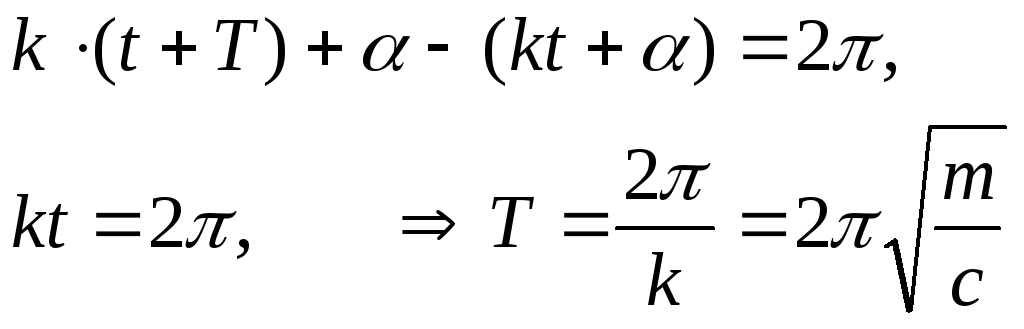
Величина, обратная периоду T, называется частотой колебания υ.

Частота – время одного полного колебания.

- количество полных колебаний за время 2π секунд

2. Затухающее колебание материальной точки

При затухающих колебаниях кроме восстанавливающей силы учитывается сила сопротивления.

, где μ – коэффициент сопротивления

Дифференциальное уравнение:

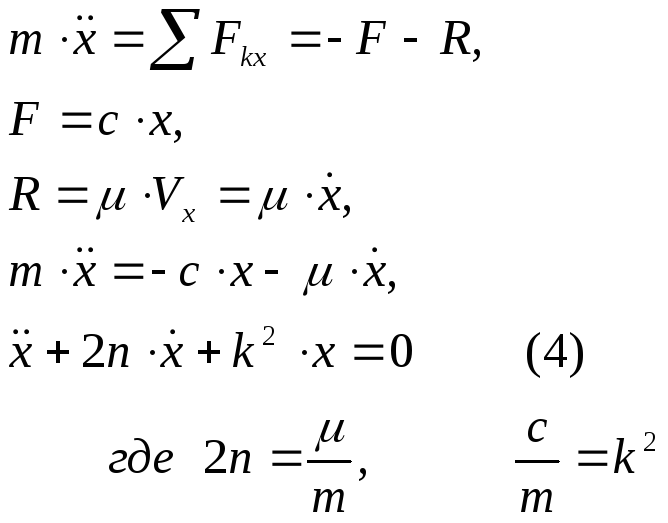
(4) - дифференциальное уравнение затухающего колебания.

Запишем характеристическое уравнение:

Корни: .

Возможны 3 случая:

1) 1-ый случай, когда n<k (малое сопротивление)

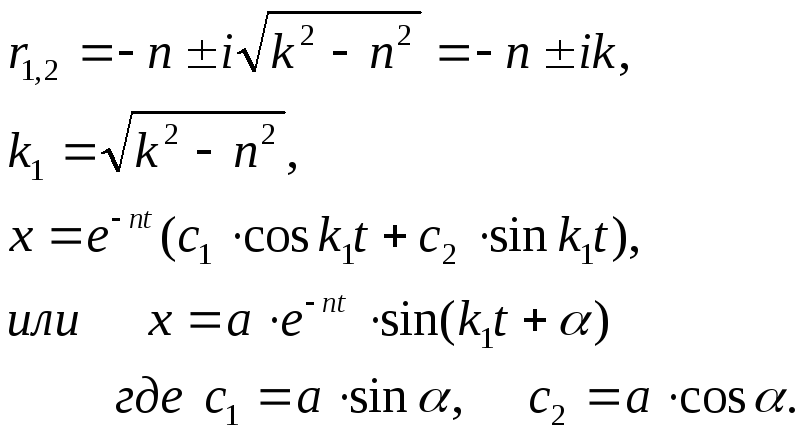
Это колебательное периодическое движение,

где k1 – круговая частота затухающих колебаний,

a - амплитуда, α - начальная фаза.

Постоянные с1 ,с2 или α и a определяются из начальных условий.

Т1 – период затухающих колебаний

В случае малого сопротивления получаем затухающее колебание точки с периодом T1:

.

Максимальное отклонение точки от равновесного положения через период или через половину периода подчиняется закону геометрической прогрессии, знаменатель которой равен или . Этот знаменатель геометрической прогрессии называется декрементом затухающих колебаний и показывает, во сколько раз отличаются амплитуды колебаний, взятые через период или через половину периода.

Логарифмический декремент затухания: или .

2) 2-ой случай, когда n>k (большое сопротивление)

Постоянные с1 и с2 определяются из начальных условий.

В этом случае движение апериодическое.

1 – толчок вперед;

2 – слабый толчок назад;

3 – сильный толчок назад.

3) 3-ий случай, когда n=k (предельный случай)

Движение апериодическое.

Постоянные с1 и с2 определяются из начальных условий.