Показатели вариации признака

Для характеристики размера вариации признака используются абсолютные и относительные показатели. К абсолютным показателям вариации относятся:

• размах колебаний;

• среднее линейное отклонение;

• среднее квадратическое отклонение;

• дисперсия;

• квартильное отклонение.

Формулы расчета абсолютных показателей вариации следующие:

Размах вариации:

, (5.14)

где соответственно максимальное и минимальное значения признака.

Среднее линейное отклонение:

. (5.15)

Дисперсия:

. (5.16)

Среднее квадратическое отклонение:

. (5.16) Формулы расчета относительных показателей вариации следующие:

Коэффициент осцилляции:

. (5.18)

Линейный коэффициент вариации:

. (5.19)

Коэффициент вариации:

. (5.20)

Относительный показатель квартильной вариации:

, (5.21)

где - среднее квартильное расстояние;

; (5.22)

; (5.23)

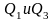- соответственно первая и третья квартили распределения;

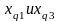- нижние границы интервалов, в которых находятся первая и третья квартили;

- ширины интервалов первой и третьей квартили;

и - сумма накопленных частостей в интервалах предшествующих интервалам, в которых находятся первая и третья квартили;

- частости интервалов, в которых находятся первая и третья квартиль.

В практике из показателей вариации получили широкое применение дисперсия, среднее квадратическое отклонение и коэффициент вариации.

Сложение дисперсий изучаемого признака.

Изучая дисперсию интересующего нас признака в пределах исследуемой совокупности и опираясь на общую среднюю в расчетах, нельзя оценить влияние отдельных факторов, определяющих вариацию индивидуальных значений (вариант) признака. Это можно сделать при помощи метода группировок, когда единицы изучаемой совокупности подразделяются на однородные группы по признаку- фактору. При этом, кроме общей средней для всей совокупности, исчисляются средние по отдельным группам (групповые или частные средние) и три показателя дисперсии:

• общая дисперсия;

• межгрупповая дисперсия;

• средняя внутригрупповая дисперсия.

Величина общей дисперсии ( ) характеризует вариацию признака под влиянием всех факторов, формирующих уровень признака у единиц данной совокупности, и определяется по формуле:

, (5.24)

где — общая средняя арифметическая для всей изучаемой совокупности.

Межгрупповая дисперсия отражает систематическую вариацию, т. е. те различия в величине изучаемого признака, которые возникают под влиянием фактора, положенного в основу группировки (графа 14 табл. 5.2). Межгрупповая дисперсия определяется по формуле:

, (5.25)

где , — средняя по отдельной группе (графа 13 табл. 5.2);

, — число единиц в определенной группе.

Средняя внутригрупповая дисперсия ( ) характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия (признака-фактора), положенного в основу группировки.

Средняя внутригрупповая дисперсия определяется по формуле:

, (5.26)

где —дисперсия в j-ой группе (графа 14 табл. 5.2), вычисляемая по формуле:

. (5.27)

Указанные дисперсии взаимосвязаны между собой следующим равенством: величина общей дисперсии равна сумме межгрупповой дисперсии и средней внутригрупповой дисперсии:

. (5.28)

Это тождество отражает закон (правило) сложения дисперсий. Опираясь на это правило, можно определить, какая часть (доля) общей дисперсии складывается под влиянием признака- фактора, положенного в основу группировки.

Вариация альтернативного признака.

Альтернативный признак - качественный признак, имеющий две взаимоисключающие разновидности (например, работники предприятия подразделяются на мужчин и женщин; продукция — на годную и бракованную и т. д.).

Альтернативный признак принимает всего два значения:

1 — наличие признака;

0 — отсутствие признака.

,

где р — доли единиц, обладающих признаком;

q - доли единиц, не обладающих признаком.

Среднее значение альтернативного признака:

. (5.29)

Дисперсия альтернативного признака:

. (5.30)

Среднее квадратическое отклонение альтернативного признака:

.

Коэффициент вариации альтернативного признака:

.

Предельное значение вариации альтернативного признака равно 0,25; оно получается при p =q = 0,5.