Математическая статистика

  ЗАДАНИЕ N 34 сообщить об ошибке Тема: Характеристики вариационного ряда Мода вариационного ряда  1, 3, 3, 4, 5, 5, 5, 7, 7, 8, 9  равна …

Решение: Модой вариационного ряда называется варианта, имеющая наибольшую частоту. Такой вариантой является варианта , частота которой равна трем.

  ЗАДАНИЕ N 26 сообщить об ошибке Тема: Интервальные оценки параметров распределения Дан доверительный интервал (25,44; 26,98) для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении надежности (доверительной вероятности) оценки доверительный интервал может принять вид …

			(24,04; 28,38)
			(25,74; 26,68)
			(24,04; 26,98)
			(24,14; 28,38)

Решение: Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде симметричного интервала  где точечная оценка математического ожидания  а точность оценки  В случае увеличения надежности точность оценки ухудшается, то есть значение  будет больше 0,77.

  ЗАДАНИЕ N 35 сообщить об ошибке Тема: Интервальные оценки параметров распределения Дан доверительный интервал  для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна …

Решение: Точность интервальной оценки  определяется как , то есть

  ЗАДАНИЕ N 36 сообщить об ошибке Тема: Проверка статистических гипотез Основная гипотеза имеет вид . Тогда конкурирующей может являться гипотеза …

Решение: Конкурирующей (альтернативной) называют гипотезу, которая противоречит основной гипотезе. Условию  противоречит .

  ЗАДАНИЕ N 37 сообщить об ошибке Тема: Точечные оценки параметров распределения В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 10, 12, 14. Тогда выборочная дисперсия равна …

			12
			0

Решение: Выборочная дисперсия вычисляется по формул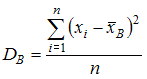е , где 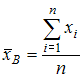  . Вычислив предварительно , получаем

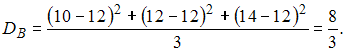
  ЗАДАНИЕ N 27 сообщить об ошибке Тема: Проверка статистических гипотез Для проверки нулевой гипотезы  при заданном уровне значимости  выдвинута конкурирующая гипотеза . Тогда область принятия гипотезы может иметь вид …

Решение: Область принятия гипотезы в данном случае определяется соотношением вида . Таким соотношением является, например .

  ЗАДАНИЕ N 28 сообщить об ошибке Тема: Элементы корреляционного анализа Выборочное уравнение прямой линии регрессии Y на X имеет вид  Тогда выборочный коэффициент корреляции может быть равен …

			– 0,67
			– 1,6
			0,74
			1,6

Решение: Значение выборочного коэффициента корреляции, во-первых, принадлежит промежутку  а во-вторых, его знак совпадает со знаком выборочного коэффициента регрессии. Этим условиям удовлетворяет значение

  ЗАДАНИЕ N 40 сообщить об ошибке Тема: Характеристики вариационного ряда Медиана вариационного ряда  2, 3, 3, 4, 5, 6, 8, 10, 12 равна …

Решение: Медианой вариационного ряда называется значение признака генеральной совокупности, приходящееся на середину вариационного ряда. В данном случае это варианта, расположенная в середине вариационного ряда. В середине данного ряда располагается варианта 5.

  ЗАДАНИЕ N 29 сообщить об ошибке Тема: Проверка статистических гипотез Основная гипотеза имеет вид . Тогда конкурирующей может являться гипотеза …

Решение: Конкурирующей (альтернативной) называют гипотезу, которая противоречит основной гипотезе. Условию  противоречит .

  ЗАДАНИЕ N 30 сообщить об ошибке Тема: Характеристики вариационного ряда Мода вариационного ряда  1, 2, 2, 3, 4, 4, , 7, 7, 8, 9 равна 4. Тогда значение  равно …

Решение: Модой вариационного ряда называется варианта, имеющая наибольшую частоту. Если модой является варианта, равная 4, то ее частота должна быть больше двух. Следовательно, , и частота этой варианты будет тогда равна трем.

  ЗАДАНИЕ N 31 сообщить об ошибке Тема: Интервальные оценки параметров распределения Дан доверительный интервал  для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …

Решение: Интервальная оценка математического ожидания нормально распределенного количественного признака представляет собой интервал, симметричный относительно точечной оценки. Тогда точечная оценка будет равна

  ЗАДАНИЕ N 32 сообщить об ошибке Тема: Точечные оценки параметров распределения Из генеральной совокупности извлечена выборка объема : 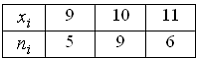Тогда несмещенная оценка математического ожидания равна …

Решение: Несмещенная оценка математического ожидания вычисляется по формуле 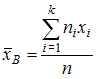. То есть