Дифференциальные уравнения

  ЗАДАНИЕ N 5 сообщить об ошибке Тема: Типы дифференциальных уравнений Уравнение  является …

			уравнением с разделяющимися переменными
			линейным неоднородным дифференциальным уравнением 2-го порядка
			однородным относительно  и  дифференциальным уравнением первого порядка
			уравнением Бернулли

Решение: Данное уравнение можно представить в виде . Откуда . Следовательно, это уравнение является уравнением с разделяющимися переменными.

  ЗАДАНИЕ N 10 сообщить об ошибке Тема: Задача Коши для дифференциального уравнения первого порядка Интегральная кривая уравнения  проходящая через точку  имеет вид …

Решение: Запишем уравнение в виде  Проинтегрировав обе части уравнения, получим:  где  Для вычисления значения C подставим в найденное решение координаты точки   Тогда 4 = 2C и C = 2. Следовательно, уравнение кривой имеет вид

  ЗАДАНИЕ N 7 сообщить об ошибке Тема: Дифференциальные уравнения с разделяющимися переменными Общее решение дифференциального уравнения  имеет вид …

			,
			,
			,
			,

Решение: Разделим переменные в исходном уравнении 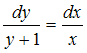 и проинтегрируем обе части последнего равенства: . Тогда , где постоянная интегрирования . Откуда , .

  ЗАДАНИЕ N 8 сообщить об ошибке Тема: Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами Общее решение линейного однородного дифференциального уравнения второго порядка  имеет вид …

Решение: Составим характеристическое уравнение  и решим его: . Тогда общее решение исходного уравнения примет вид: .

  ЗАДАНИЕ N 11 сообщить об ошибке Тема: Однородные дифференциальные уравнения Общее решение дифференциального уравнения  имеет вид …

			, где
			где
			где
			где

Решение: Запишем уравнение в виде  Сделаем замену   Тогда    и уравнение примет вид: Разделив переменные, получим: Проинтегрируем обе части последнего уравнения:  где Тогда  Сделаем обратную замену:

  ЗАДАНИЕ N 14 сообщить об ошибке Тема: Дифференциальные уравнения с разделяющимися переменными Общее решение дифференциального уравнения  имеет вид …

			,
			,
			,
			,

Решение: Разделим переменные в исходном уравнении  и проинтегрируем обе части последнего равенства: . Тогда , где постоянная интегрирования . Откуда , .

  ЗАДАНИЕ N 15 сообщить об ошибке Тема: Задача Коши для дифференциального уравнения первого порядка Функция  является общим решением дифференциального уравнения 1-го порядка. Тогда для начального условия  частное решение этого уравнения имеет вид …

Решение: Подставив в общее решение начальное условие , то есть , получим значение . Следовательно, искомое частное решение имеет вид .

  ЗАДАНИЕ N 16 сообщить об ошибке Тема: Типы дифференциальных уравнений Уравнение  является …

			уравнением с разделяющимися переменными
			линейным дифференциальным уравнением 1-го порядка
			однородным относительно  и  дифференциальным уравнением первого порядка
			уравнением Бернулли

Решение: Данное уравнение можно представить в виде . Откуда . Следовательно, это уравнение является уравнением с разделяющимися переменными.

  ЗАДАНИЕ N 12 сообщить об ошибке Тема: Типы дифференциальных уравнений Уравнение  является …

			однородным относительно x и y дифференциальным уравнением первого порядка
			линейным неоднородным дифференциальным уравнением первого порядка
			уравнением Бернулли
			дифференциальным уравнением с разделяющимися переменными

Решение: В уравнении  функция  является однородной относительно  и  функцией нулевого порядка. Действительно,   Поэтому данное уравнение является однородным относительно x и y дифференциальным уравнением первого порядка.

  ЗАДАНИЕ N 27 сообщить об ошибке Тема: Типы дифференциальных уравнений Уравнение  является …

			линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами
			линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами
			уравнением Бернулли
			дифференциальным уравнением с разделяющимися переменными

Решение: Уравнение  можно представить в виде , где  и  – числа. Поэтому данное уравнение является линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами.

  ЗАДАНИЕ N 28 сообщить об ошибке Тема: Задача Коши для дифференциального уравнения первого порядка Решение задачи Коши , имеет вид …

Решение: Проинтегрировав обе части уравнения, получим: . Тогда общее решение исходного уравнения имеет вид . Для вычисления значения  подставим в найденное общее решение начальное условие . Тогда  и . Следовательно, частное решение имеет вид .