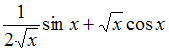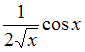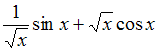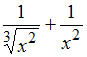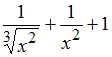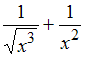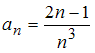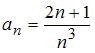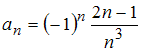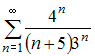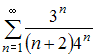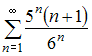Дифференциальное и интегральное исчисление
ЗАДАНИЕ N 36 сообщить
об ошибке
Тема: Свойства
определенного интеграла
Среднее
значение функции
![]() на
отрезке
на
отрезке
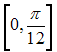 равно …
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Среднее
значение функции
![]() непрерывной
на отрезке
непрерывной
на отрезке
![]() вычисляется
по формуле
вычисляется
по формуле
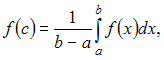 где
где
![]() Тогда
Тогда

ЗАДАНИЕ N 17 сообщить
об ошибке
Тема: Методы
вычисления определенного
интеграла
Определенный
интеграл
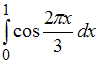 равен …
равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Для
вычисления данного определенного
интеграла произведем замену переменных:
![]() ,
,
![]() ,
,
![]() ,
и перейдем к новым пределам интегрирования:
,
и перейдем к новым пределам интегрирования:
![]() ,
,
![]() .
Тогда
.
Тогда
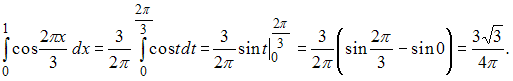
ЗАДАНИЕ N 18 сообщить
об ошибке
Тема: Дифференциальное
исчисление ФНП
Полный
дифференциал функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Полный
дифференциал функции нескольких
переменных равен сумме произведений
частных производных этой функции на
дифференциалы соответствующих независимых
переменных, то есть
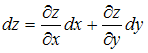 .
Тогда
.
Тогда
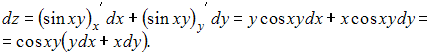
ЗАДАНИЕ N 37 сообщить
об ошибке
Тема: Дифференциальное
исчисление ФНП
Приближенное
значение функции
![]() в
точке
в
точке
![]() вычисленное
с помощью полного дифференциала, равно …
вычисленное
с помощью полного дифференциала, равно …
|
|
|
0,51 |
|
|
|
1,71 |
|
|
|
4,29 |
|
|
|
0,45 |
Решение:
Воспользуемся
формулой
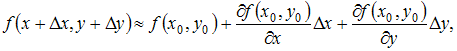 где
где
![]()
![]()
![]()
![]() Вычислим
последовательно
Вычислим
последовательно
![]()
![]()
![]()
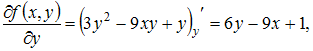
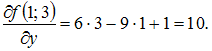 Тогда
Тогда
![]()
ЗАДАНИЕ N 19 сообщить
об ошибке
Тема: Производные
первого порядка
Производная
функции
![]() равна …
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
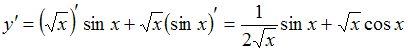 .
.
ЗАДАНИЕ N 20 сообщить
об ошибке
Тема: Предел
функции
Предел
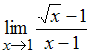 равен …
равен …
|
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
|
|
Решение:
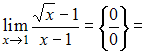 Для
раскрытия этой неопределенности умножим
числитель и знаменатель на выражение,
сопряженное числителю, то есть на
Для
раскрытия этой неопределенности умножим
числитель и знаменатель на выражение,
сопряженное числителю, то есть на
![]() :
:
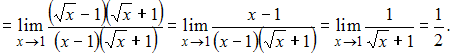
ЗАДАНИЕ N 14 сообщить
об ошибке
Тема: Дифференциальное
исчисление ФНП
Частная
производная
![]() функции
функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
При
вычислении частной производной
по
переменной
,
переменную
![]() рассматриваем
как постоянную величину. Тогда
рассматриваем
как постоянную величину. Тогда
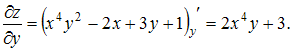
ЗАДАНИЕ N 16 сообщить
об ошибке
Тема: Методы
вычисления определенного
интеграла
Определенный
интеграл
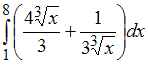 равен …
равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Для
вычисления определенного интеграла
применим формулу Ньютона-Лейбница:
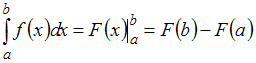 ,
где
,
где
![]() –
первообразная функции
–
первообразная функции
![]() .
Тогда
.
Тогда
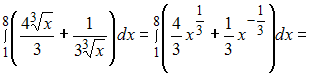
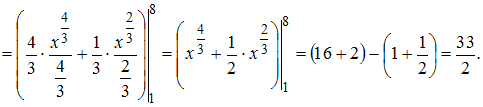
ЗАДАНИЕ N 9 сообщить
об ошибке
Тема: Предел
функции
Предел
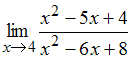 равен …
равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
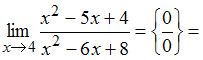 Разложим
числитель и знаменатель на линейные
множители как
Разложим
числитель и знаменатель на линейные
множители как
![]() и
и
![]() .
.
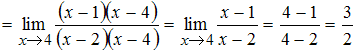 .
.
ЗАДАНИЕ N 10 сообщить
об ошибке
Тема: Методы
вычисления определенного
интеграла
Определенный
интеграл
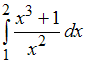 равен …
равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Для
вычисления определенного интеграла
применим формулу Ньютона-Лейбница:
,
где
–
первообразная функции
.
Тогда
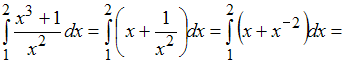
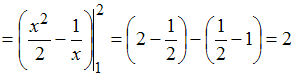 .
.
ЗАДАНИЕ N 11 сообщить
об ошибке
Тема: Производные
первого порядка
Производная
функции
![]() равна …
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
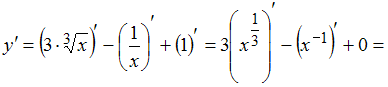
 .
.
ЗАДАНИЕ N 12 сообщить
об ошибке
Тема: Дифференциальное
исчисление ФНП
Частная
производная второго порядка
![]() функции
функции
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
При
вычислении частной производной функции
![]() по
одной из переменных другую переменную
рассматриваем как постоянную величину.
Тогда
по
одной из переменных другую переменную
рассматриваем как постоянную величину.
Тогда
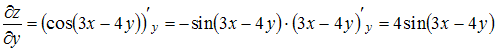 и
и

![]()
Ряды
ЗАДАНИЕ N 21 сообщить
об ошибке
Тема: Область
сходимости степенного ряда
Область
сходимости степенного ряда
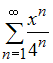 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Вычислим
предварительно радиус сходимости этого
ряда по формуле
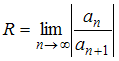 ,
где
,
где
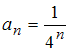 .
Тогда
.
Тогда
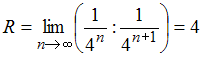 .
Следовательно, интервал сходимости
ряда имеет вид
.
Следовательно, интервал сходимости
ряда имеет вид
![]() .
Для
того чтобы найти область сходимости
степенного ряда, исследуем сходимость
ряда в граничных точках.
В точке
.
Для
того чтобы найти область сходимости
степенного ряда, исследуем сходимость
ряда в граничных точках.
В точке
![]() ряд
примет вид
ряд
примет вид
![]() .
Данный ряд расходится, так как не
выполняется необходимое условие
сходимости числового ряда:
.
Данный ряд расходится, так как не
выполняется необходимое условие
сходимости числового ряда:
![]() В
точке
В
точке
![]() получаем
знакочередующийся ряд
получаем
знакочередующийся ряд
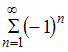 .
Аналогично получаем
.
Аналогично получаем
![]() ,
то есть ряд расходится.
Таким образом,
область сходимости ряда имеет вид
.
,
то есть ряд расходится.
Таким образом,
область сходимости ряда имеет вид
.
ЗАДАНИЕ N 22 сообщить
об ошибке
Тема: Ряд Тейлора
(Маклорена)
Если
![]() ,
то коэффициент
,
то коэффициент
![]() разложения
данной функции в ряд Маклорена по
степеням
равен …
разложения
данной функции в ряд Маклорена по
степеням
равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Так
как коэффициенты данного ряда вычисляются
по формуле
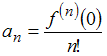 ,
то вычислим последовательно
производные:
,
то вычислим последовательно
производные:
![]()
![]()
![]() .
Тогда
.
Тогда
![]()
ЗАДАНИЕ N 23 сообщить
об ошибке
Тема: Числовые
последовательности
Числовая
последовательность задана рекуррентным
соотношением
![]() ,
,
![]() .
Тогда
.
Тогда
![]() равно …
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Вычислим
последовательно:
![]() ,
,
![]() ,
,
![]() .
.
ЗАДАНИЕ N 24 сообщить
об ошибке
Тема: Сходимость
числовых рядов
Даны
числовые ряды:
А)
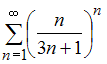 ,
В)
,
В)
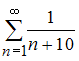 .
Тогда …
.
Тогда …
|
|
|
ряд А) сходится, ряд В) расходится |
|
|
|
ряд А) расходится, ряд В) расходится |
|
|
|
ряд А) сходится, ряд В) сходится |
|
|
|
ряд А) расходится, ряд В) сходится |
Решение:
Для
исследования сходимости ряда
применим
радикальный признак сходимости Коши.
Тогда
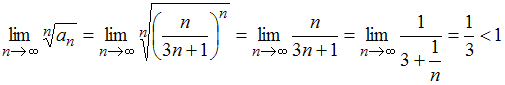 ,
то есть ряд сходится.
Для исследования
сходимости ряда
,
то есть ряд сходится.
Для исследования
сходимости ряда
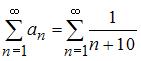 применим
теорему сравнения, для чего воспользуемся
расходящимся гармоническим рядом
применим
теорему сравнения, для чего воспользуемся
расходящимся гармоническим рядом
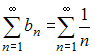 .
Тогда
.
Тогда
 ,
то есть оба ряда расходятся или сходятся
одновременно. В нашем случае ряд
будет
расходится.
,
то есть оба ряда расходятся или сходятся
одновременно. В нашем случае ряд
будет
расходится.
ЗАДАНИЕ
N 25 сообщить
об ошибке
Тема: Числовые
последовательности
Общий
член числовой последовательности
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 26 сообщить
об ошибке
Тема: Сходимость
числовых рядов
Сумма
числового ряда
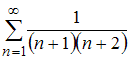 равна …
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Представим
общий член этого ряда в виде суммы
простейших дробей:
 ,
и вычислим
,
и вычислим
![]() –
ую частичную сумму ряда:
–
ую частичную сумму ряда:
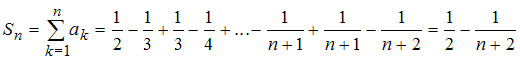 .
Тогда
.
Тогда
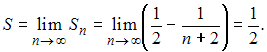
ЗАДАНИЕ N 27 сообщить
об ошибке
Тема: Ряд Тейлора
(Маклорена)
Если
![]() ,
то коэффициент
,
то коэффициент
![]() разложения
данной функции в ряд Тейлора по степеням
разложения
данной функции в ряд Тейлора по степеням
![]() равен …
равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Так
как коэффициенты данного ряда Тейлора
вычисляются по формуле
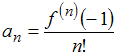 ,
то вычислим последовательно производные:
,
то вычислим последовательно производные:
![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
.
ЗАДАНИЕ N 33 сообщить
об ошибке
Тема: Числовые
последовательности
Числовая
последовательность задана формулой
общего члена
![]() .
Тогда значение
.
Тогда значение
![]() равно …
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Подставим
в формулу общего члена значение
![]() .
Тогда
.
Тогда
![]() .
.
ЗАДАНИЕ
N 34 сообщить
об ошибке
Тема: Ряд Тейлора
(Маклорена)
Разложение
в ряд Маклорена функции
![]() имеет
вид:
имеет
вид:
![]() Тогда
для функции
Тогда
для функции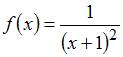 ,
коэффициент
,
коэффициент
![]() разложения
данной функции в ряд Маклорена равен …
разложения
данной функции в ряд Маклорена равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 35 сообщить
об ошибке
Тема: Сходимость
числовых рядов
Сумма
числового ряда
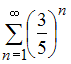 равна …
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Так
как
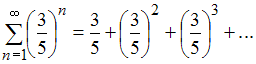 ,
то сумма данного ряда представляет
собой сумму бесконечно убывающей
геометрической прогрессии. То есть
,
то сумма данного ряда представляет
собой сумму бесконечно убывающей
геометрической прогрессии. То есть
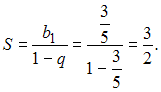
ЗАДАНИЕ N 13 сообщить об ошибке Тема: Сходимость числовых рядов Расходящимся является числовой ряд …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Из
представленных числовых рядов расходящимся
является ряд
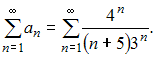 Действительно,
так как при применении признака Даламбера,
получаем:
Действительно,
так как при применении признака Даламбера,
получаем:
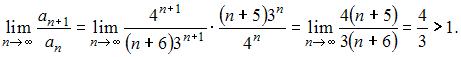 Для
остальных рядов аналогичный предел
будет принимать значения, меньшие
единицы.
Для
остальных рядов аналогичный предел
будет принимать значения, меньшие
единицы.