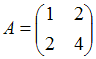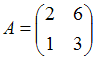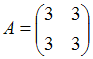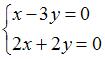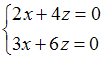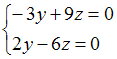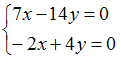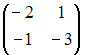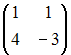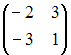Специальность: 080109.65 - Бухгалтерский учет, анализ и аудит
Специальность: 080105.65 - Финансы и кредит Дисциплина: Математика Количество заданий в тесте: 38
Время, отведенное для выполнения заданий теста: 76 мин.
N |
Дидактическая единица |
Процент студентов, освоивших ДЕ |
1 |
Линейная алгебра |
62% |
2 |
Аналитическая геометрия |
38% |
3 |
Дифференциальное и интегральное исчисление |
33% |
4 |
Ряды |
57% |
5 |
Дифференциальные уравнения |
33% |
6 |
Теория вероятностей |
52% |
7 |
Математическая статистика |
52% |
8 |
Экономико-математические методы |
38% |
9 |
Экономико-математические модели |
38% |
Линейная алгебра
![]() ЗАДАНИЕ N 8 сообщить
об ошибке
Тема: Умножение
матриц
Даны
матрицы
ЗАДАНИЕ N 8 сообщить
об ошибке
Тема: Умножение
матриц
Даны
матрицы
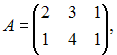
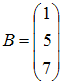 и
и
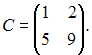 Тогда
существует произведение матриц …
Тогда
существует произведение матриц …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Произведением
матриц возможно, если число столбцов
первой матрицы равно числу строк второй.
Проверим выполнение данного условия:
1)
Для произведения
![]() условие
не выполнено, так как у матрицы B
один столбец, а у матрицы A
две строки.
2) Для произведения
условие
не выполнено, так как у матрицы B
один столбец, а у матрицы A
две строки.
2) Для произведения
![]() условие
не выполнено, так как у матрицы C
два столбца, а у матрицы B
три строки.
3) Для произведения
условие
не выполнено, так как у матрицы C
два столбца, а у матрицы B
три строки.
3) Для произведения
![]() условие
не выполнено, так как у матрицы A
три столбца, а у матрицы C
две строки.
4) Для произведения
условие
не выполнено, так как у матрицы A
три столбца, а у матрицы C
две строки.
4) Для произведения
![]() условие
выполнено, так как размерность матрицы
C
– 2×2, матрицы A
– 2×3 и матрицы B
– 3×1. То есть число столбцов матрицы C
равно числу строк матрицы A,
а число столбцов матрицы A
равно числу строк матрицы B.
условие
выполнено, так как размерность матрицы
C
– 2×2, матрицы A
– 2×3 и матрицы B
– 3×1. То есть число столбцов матрицы C
равно числу строк матрицы A,
а число столбцов матрицы A
равно числу строк матрицы B.
ЗАДАНИЕ N 21 сообщить
об ошибке
Тема: Вычисление
определителей
Корень
уравнения
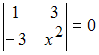 равен …
равен …
|
|
|
|
|
|
|
3 |
|
|
|
– |
|
|
|
–1 |
Решение:
Определитель
второго порядка вычисляется по формуле:
 .
Тогда
.
Тогда
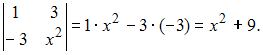 По
условию задачи определитель должен
равняться 0, то есть
По
условию задачи определитель должен
равняться 0, то есть
![]() Следовательно,
Следовательно,
![]()
![]()
ЗАДАНИЕ N 22 сообщить об ошибке Тема: Обратная матрица Обратная матрица существует для матрицы …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Всякая
невырожденная квадратная матрица имеет
обратную матрицу, то есть матрица имеет
обратную, если определитель матрицы не
равен нулю. Тогда
1)
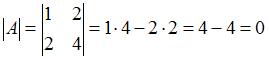 ,
то есть обратная матрица не существует.
2)
,
то есть обратная матрица не существует.
2)
 ,
то есть обратная матрица не существует.
3)
,
то есть обратная матрица не существует.
3)
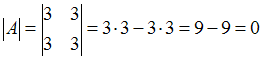 ,
то есть обратная матрица не существует.
4)
,
то есть обратная матрица не существует.
4)
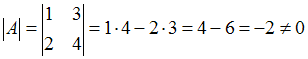 ,
следовательно, обратная матрица
существует.
,
следовательно, обратная матрица
существует.
ЗАДАНИЕ N 23 сообщить
об ошибке
Тема: Умножение
матриц
Даны
матрицы
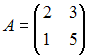 и
и
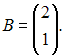 Тогда
матрица
Тогда
матрица
![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Произведением
![]() матрицы
матрицы
![]() размера
размера
![]() на
матрицу
на
матрицу
![]() размера
размера
![]() называется
матрица
называется
матрица
![]() размера
размера
![]() ,
элемент которой
,
элемент которой
![]() равен
сумме произведений соответственных
элементов i-й
строки матрицы
и
j-го
столбца матрицы
.
Тогда
равен
сумме произведений соответственных
элементов i-й
строки матрицы
и
j-го
столбца матрицы
.
Тогда
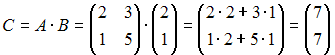 .
.
ЗАДАНИЕ N 24 сообщить об ошибке Тема: Системы линейных уравнений Единственное решение имеет однородная система линейных алгебраических уравнений …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Однородная
система линейных алгебраических
уравнений имеет одно единственное
решение, если ее определитель не равен
нулю.
1) Из системы
,
получим
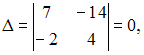 так
как столбцы пропорциональны.
2) Из
системы
,
получим
так
как столбцы пропорциональны.
2) Из
системы
,
получим
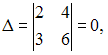 так
как строки пропорциональны.
3) Из
системы
,
получим
так
как строки пропорциональны.
3) Из
системы
,
получим
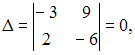 так
как строки пропорциональны.
4). Из
системы
,
получим
так
как строки пропорциональны.
4). Из
системы
,
получим
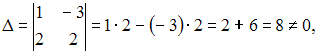 следовательно,
система имеет одно единственное решение.
следовательно,
система имеет одно единственное решение.
ЗАДАНИЕ N 2 сообщить
об ошибке
Тема: Вычисление
определителей
Корень
уравнения
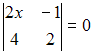 равен …
равен …
|
|
|
– 1 |
|
|
|
1 |
|
|
|
4 |
|
|
|
– 4 |
Решение:
Определитель
второго порядка вычисляется по формуле:
.
Тогда
 По
условию задачи определитель должен
равняться 0, то есть
По
условию задачи определитель должен
равняться 0, то есть
![]() Следовательно,
Следовательно,
![]()
ЗАДАНИЕ N 4 сообщить
об ошибке
Тема: Обратная
матрица
Для
матрицы
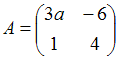 не
существует
обратной, если значение
не
существует
обратной, если значение
![]() равно …
равно …
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
– 2 |
Решение:
Матрица
не имеет обратной, если определитель
матрицы равен нулю, то есть
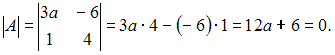 Тогда
обратной матрицы не существует при
Тогда
обратной матрицы не существует при
![]()
ЗАДАНИЕ N 13 сообщить об ошибке Тема: Обратная матрица Обратная матрица существует для матрицы …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Всякая невырожденная квадратная матрица имеет обратную матрицу, то есть матрица имеет обратную, если определитель матрицы не равен нулю. Тогда 1) , то есть обратная матрица не существует. 2) , то есть обратная матрица не существует. 3) , то есть обратная матрица не существует. 4) , следовательно, обратная матрица существует.
ЗАДАНИЕ N 15 сообщить
об ошибке
Тема: Умножение
матриц
Даны
матрицы
и
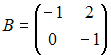 .
Тогда матрица
имеет
вид …
.
Тогда матрица
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Произведением
матрицы
размера
на
матрицу
размера
называется
матрица
размера
,
элемент которой
равен
сумме произведений соответственных
элементов i-й
строки матрицы
и
j-го
столбца матрицы
.
Тогда
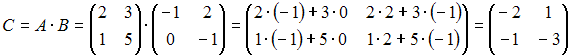 .
.
ЗАДАНИЕ N 16 сообщить
об ошибке
Тема: Системы
линейных уравнений
Система
линейных уравнений
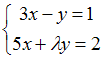 не
имеет решений,
если
не
имеет решений,
если
![]() равно …
равно …
|
|
|
|
|
|
|
|
|
|
|
2,4 |
|
|
|
– 2,4 |
Решение:
Система
линейных уравнений
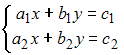 не
имеет решений, если определитель матрицы
системы
не
имеет решений, если определитель матрицы
системы
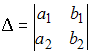 равен
нулю, а хотя бы один из определителей
равен
нулю, а хотя бы один из определителей
 или
или
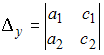 нулю
не равен.
Например,
нулю
не равен.
Например,
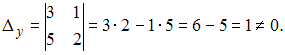 Следовательно,
система не имеет решений, когда
Следовательно,
система не имеет решений, когда
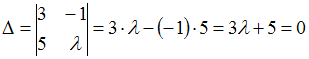 и
и
![]()