
Яблонский Задачи по динамике1 / Задача Д2
.docxЗадача Д2
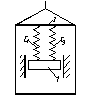
Груз 1 массой
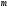 укреплен на пружинной подвеске в лифте.
Лифт движется вертикально по закону
укреплен на пружинной подвеске в лифте.
Лифт движется вертикально по закону
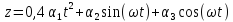 (ось z направлена по
вертикали вверх; z выражено
в метрах, t – в секундах).
На груз действует сила сопротивления
(ось z направлена по
вертикали вверх; z выражено
в метрах, t – в секундах).
На груз действует сила сопротивления

Найти закон движения груза по отношению
к лифту, т.е.
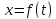 ;
начало координат поместить в точке, где
находится прикрепленный к грузу конец
пружины, когда пружина не деформирована.
Ось х направить в сторону удлинения
пружины, а груз изобразить в положении,
при котором х>0, т.е. пружина растянута.
Принять g=10 м/с2.
Массой пружин и соединительной планки
2 пренебречь.
;
начало координат поместить в точке, где
находится прикрепленный к грузу конец
пружины, когда пружина не деформирована.
Ось х направить в сторону удлинения
пружины, а груз изобразить в положении,
при котором х>0, т.е. пружина растянута.
Принять g=10 м/с2.
Массой пружин и соединительной планки
2 пренебречь.
с1 и с3 – коэффициенты
жесткости пружин, λ0 – удлинение
пружины с эквивалентной жесткостью в
начальный момент времени t=0,
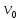 -
начальная скорость груза по отношению
к лифту (направлена вертикально вверх).
-
начальная скорость груза по отношению
к лифту (направлена вертикально вверх).
Условие
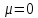 означает, что сила сопротивления R
отсутствует.
означает, что сила сопротивления R
отсутствует.
|
Дано: m=1кг с1=240 Н/м с3=160 Н/м
λ0=0 υ0=0
|
Решение:
1.Заменим прикрепленные
к грузу пружины одной эквивалентной
пружиной с коэффициентом жесткости
сэк=с. Каждая из
пружин и эквивалентная пружина при
равновесии имеют одно и то же удлинение
λ. Для двух пружин
|
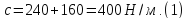
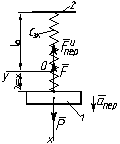
2.Составим дифференциальное уравнение
относительного движения груза (по
отношению к лифту). Свяжем с лифтом
подвижную систему отсчета, начало
которой О поместим в конце недеформированной
пружины, а ось x направим
в сторону удлинения пружины. l0-
длина эквивалентной пружины в
недеформированном состоянии. Рассмотрим
груз в положении, при котором пружина
растянута. На груз действует сила тяжести
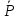 и сила упругости
и сила упругости
 .
Переносная сила инерции
.
Переносная сила инерции
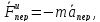 кориолисова сила инерции равна нулю,
так как переносное движение (движение
лифта) является поступательным.
кориолисова сила инерции равна нулю,
так как переносное движение (движение
лифта) является поступательным.
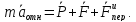
Проектируя обе части на ось x, получим
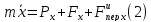
 ,
где λ = x – удлинение
пружины,
,
где λ = x – удлинение
пружины,
 .
Учитывая, что оси x
и z направлены в
противоположные стороны, получим
.
Учитывая, что оси x
и z направлены в
противоположные стороны, получим
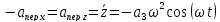 и
и
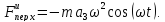
Подставим найденные выражения в уравнение (2)

Дифференциальное уравнение (3) запишем в виде:
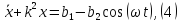
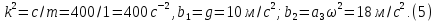
2.Для определения закона движения груза проинтегрируем уравнение (4)
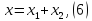
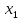 – общее решение однородного уравнения
– общее решение однородного уравнения
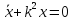 ,
т.е.
,
т.е.
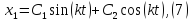
 – частное решение уравнения (4).
– частное решение уравнения (4).
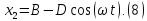
Находим
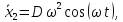 подставляем значения
подставляем значения
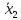 и
и
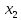 в уравнение (4) и приравниваем в его обеих
частях свободные члены и коэффициенты
при
в уравнение (4) и приравниваем в его обеих
частях свободные члены и коэффициенты
при
 .
.

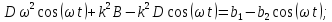
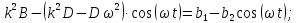

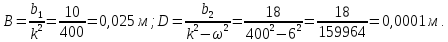
Общее решение уравнения (4) (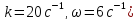
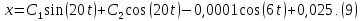
Для определения C1
и C2 найдем
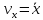 ;
;
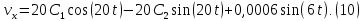
Подставим в уравнения (9) и (10) начальные
данные t=0,
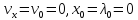
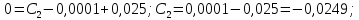
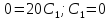
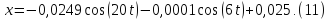
Ответ:
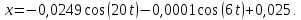

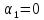
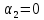
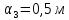
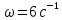
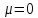
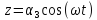
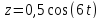
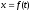 -?
-?
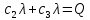 ,
для эквивалентной пружины
,
для эквивалентной пружины
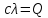 ,
отсюда
,
отсюда
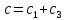 .
.