
Яблонский Задачи по динамике1 / Задача Д5
.docxЗадача Д5
Однородная горизонтальная платформа
(прямоугольная со сторонами R
и 2R, где R=1,2
м) массой m1=24 кг
вращается с угловой скоростью
 вокруг вертикальной оси z,
отстоящей от центра масс C
платформы на расстоянии OC=b.
вокруг вертикальной оси z,
отстоящей от центра масс C
платформы на расстоянии OC=b.
В момент времени t0=0 по желобу платформы начинает двигаться (под действием внутренних сил) груз D массой m2=8 кг по закону s=AD=F(t), где s выражено в метрах, t – в секундах. Одновременно на платформы начинает действовать пара сил с моментом M (задан в ньютонометрах; при M<0 его направление противоположно показанному на рисунке).
Определить, пренебрегая массой вала,
зависимость
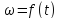 ,
т.е. угловую скорость платформы, как
функцию времени.
,
т.е. угловую скорость платформы, как
функцию времени.

|
Дано:
m1=24 кг m2=8 кг t0=0 R=1,2 м
OC=b=R/2=0,6 м s=AD=F(t)=10t M= - 8t
|
Решение:
Для определения
|

На систему действуют внешние силы: силы
тяжести
 , реакции
, реакции
 и вращающий момент M.
Так как силы
и вращающий момент M.
Так как силы
 параллельны оси z, а реакции
параллельны оси z, а реакции
 эту ось пересекают, то их моменты
относительно оси z равны
нулю.
эту ось пересекают, то их моменты
относительно оси z равны
нулю.


Умножая обе части этого уравнения на dt и интегрируя, получим

Для рассматриваемой механической системы

где
 - кинетические моменты платформы и груза
D соответственно.
- кинетические моменты платформы и груза
D соответственно.
Так как платформа вращается вокруг оси
z, то
 .
.
 - найдем по формуле Гюйгенса:
- найдем по формуле Гюйгенса:

где
 - момент инерции относительно оси
- момент инерции относительно оси
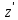 ,
параллельной оси
,
параллельной оси
 и проходящей через центр С платформы.
и проходящей через центр С платформы.

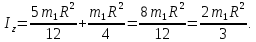


Для определения
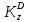 рассмотрим движение груза D
как сложное, считая его движение по
платформе относительным, а вращение
самой платформы вокруг оси z
переносным движением. Тогда абсолютная
скорость груза
рассмотрим движение груза D
как сложное, считая его движение по
платформе относительным, а вращение
самой платформы вокруг оси z
переносным движением. Тогда абсолютная
скорость груза
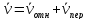 .
Так как груз D движется
по закону s=AD=F(t)=10t,
то
.
Так как груз D движется
по закону s=AD=F(t)=10t,
то


По теореме Вариньона

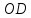 найдем
по теореме косинусов (
найдем
по теореме косинусов (



Подставим эту величину в равенство (6)
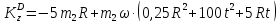
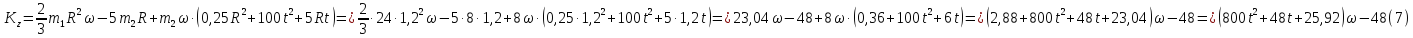
Тогда уравнение (3)

Постоянную
интегрирования определим по начальным
условиям: при t=0,
 .
.

Подставляем
значение
 в уравнение (8)
в уравнение (8)
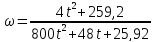
Ответ:
 где t – в секундах,
где t – в секундах,
 – в с-1.
– в с-1.


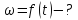

 применим теорему об изменении
кинетического момента системы
относительно оси z:
применим теорему об изменении
кинетического момента системы
относительно оси z: