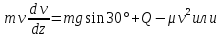Яблонский Задачи по динамике1 / Задача Д1
.docxВариант 10+13=23 (Рис.2, условие 3)
Задача Д1
Груз D массой
 ,
получив в точке А начальную скорость
υ0=14 м/с, движется в
изогнутой трубе АВС, расположенной
в вертикальной плоскости; участки трубы
один горизонтальный, а другой наклонный.
,
получив в точке А начальную скорость
υ0=14 м/с, движется в
изогнутой трубе АВС, расположенной
в вертикальной плоскости; участки трубы
один горизонтальный, а другой наклонный.
На участке АВ на груз кроме силы
тяжести действуют постоянная сила
 и сила сопротивления среды
и сила сопротивления среды
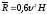 ,
зависящая от скорости υ груза (направлена
против движения); трением груза о трубу
на участке АВ пренебречь.
,
зависящая от скорости υ груза (направлена
против движения); трением груза о трубу
на участке АВ пренебречь.
В точке В груз, не изменяя своей
скорости, переходит на участок ВС
трубы, где на него кроме силы тяжести
действуют силы трения ( коэффициент
трения груза о трубу
 )
и переменная сила
)
и переменная сила
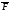 ,
проекция которой на ось х
,
проекция которой на ось х
 .
.
Считая груз материальной точкой зная
расстояние АВ=l=5
м, найти закон движения груза на
участке ВС, т.е.
 ,
где
,
где


|
Дано:
υ0=14 м/с АВ=l=5 м
|
Решение: 1.Рассмотрим
движение груза на участке АВ, считая
груз материальной точкой . Изображаем
груз и действующие на него силы
Далее
находим
|
Введем обозначение



Разделяя в уравнении (4) переменные, а затем беря от обеих частей интегралы, получим

По начальным условиям z=0,
υ =υ0, что дает
 и
из равенства (5) находим
и
из равенства (5) находим
 или
или
 Отсюда
Отсюда

В результате находим

Полагая в равенстве (6) z=l=5
м и заменяя k и n
их значениями (3), определим скорость
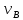 груза в точке B (υ0=14
м/с, e=2,7):
груза в точке B (υ0=14
м/с, e=2,7):
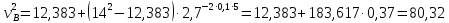

2.Рассмотрим движение груза на участке
BC;
 .
На груз будут действовать силы
.
На груз будут действовать силы
 ,
,
 ,
,
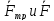 .
.
Составим дифференциальное уравнение движения груза в проекции на ось Bx:
 или
или

где
 Для определения N составим
уравнение в проекции на ось By.
Для определения N составим
уравнение в проекции на ось By.
 ;
;
 .
Подставим эти выражения в уравнение
(8):
.
Подставим эти выражения в уравнение
(8):


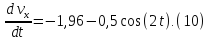
Умножаем обе части уравнения (10) на dt и интегрируем.

При t=0,


Умножаем обе части на dt и интегрируем:

При t=0 x=0, следовательно


где
 - в метрах,
- в метрах,
 - в секундах.
- в секундах.
Ответ:





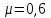


 -?
-? ,
,
 ,
,
 и
и
 .
Проводим ось Az и
составляем дифференциальное уравнение
движения груза в проекции на эту ось:
.
Проводим ось Az и
составляем дифференциальное уравнение
движения груза в проекции на эту ось: или
или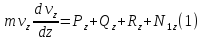
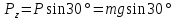 ,
,
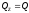 ,
,
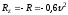 ,
,
 ,
,
 ,
получим
,
получим