МИНИСТЕРСТВО ОБРАЗОВАНИЯ

РЕСПУБЛИКИ БЕЛАРУСЬ

УО ВГТУ

Кафедра ТМ и ТММ

Расчётно-графическая работа

Тема: “ Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил.”

Вариант - 9

Выполнил: студент группы А-17 Кибисов Александр Николаевич

Проверил: Локтионов Анатолий Васильевич

2004

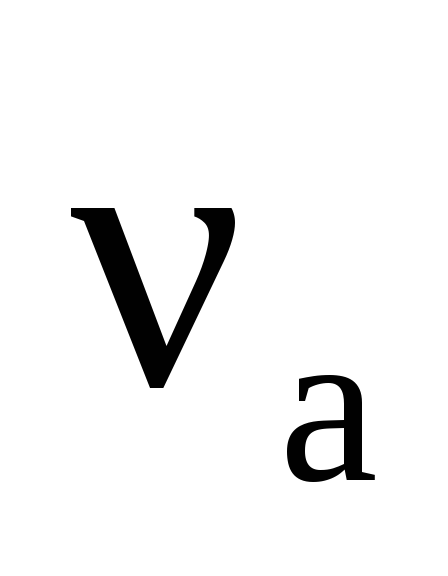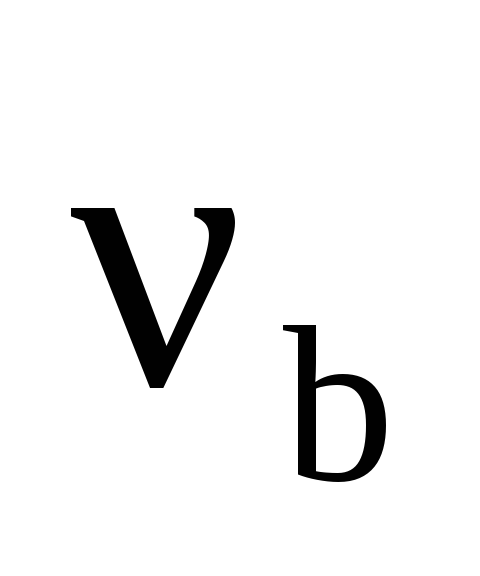Лыжник подходит к точке А участка трамплина АВ, наклонённого под углом к горизонту и имеющего длину l, со скоростью . Коэффициент трения скольжения на участке АВ равен f. Лыжник от А до В движется с; в точке В со скоростью он покидает трамплин. Через Т с лыжник приземляется со скоростью в точке С горы, составляющей угол с горизонтом.

		f	h
15	0,3с	0,1		60

Определить и .

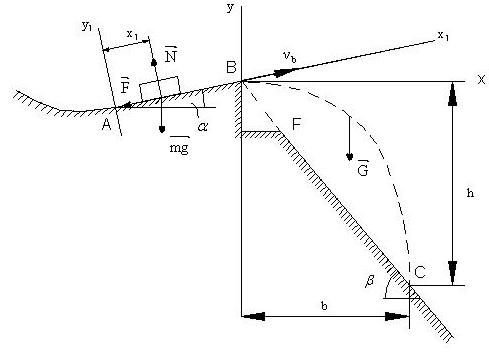
Решение.

Рассмотрим движение лыжника на участке АВ. Принимая лыжника за материальную точку,

Покажем действующие на него силы: вес , нормальную реакцию опоры и силу трения скольжения .составим дифференциальное уравнение движения лыжника на отрезке АВ:

Сила трения

F = f N,

где

N = ;

Таким образом,

или

Интегрируя уравнение дважды, получаем:

;

Для определения постоянных интегрирования воспользуемся начальными условиями зада -

чи: t = 0, х = 0, = . Получим

= , = 0.

Тогда

;

Для момента , когда лыжник покидает трамплин,

Рассмотрим движение камня от точки В до точки С.

Составим дифференциальное уравнение.

Начальные условия задачи: при t = 0

, ,

, .

Проинтегрируем дифференциальные уравнения дважды:

, ,

, .

Используя начальные данные, получим:

, ,

, .

Запишем следующие системы движения и скоростей лыжника относительно выбранных осей координат.

Уравнение траектории лыжника найдём, исключив из системы параметр t.

В точке падения х = b, а у = -h. Из теоремы Пифагора b = h ctg;

Определяем .

= 8 м/с

Тогда

= 9 м/с

Ответ: = 9 м/с , = 8 м/с.