
- •1.Предмет теории вероятностей – анализ случайных явлений: отсутствие детерминистической регулярности и наличие статистической регулярности
- •2.Теория вероятностей как аксиоматизируемая математическая дисциплина
- •2. Эксперимент (опыт, испытание, явление)и его исход (результат, наблюдение)
- •3. Вспомогательная модель. Реализация этой идеи
- •4. Вероятностная модель
- •5. Вспомогательная и Вероятностная модели экспериментов. Однократное и двукратное подбрасывания монеты
- •7. Общая схема построения конечной вероятностной модели – вероятностного пространства
- •8. Произвели эксперимент, известен исход. Произошло ли событие?
- •9. Практическое значение вероятности события
- •11. Аксиомы а.Н. Колмогорова
- •1. Элементарная теория вероятностей
- •10. Необходимые в теории вероятностей сведения из теории множеств и теории меры
- •3. Основное определение
- •12. Непосредственные следствия из аксиом
- •13. Парадокс де Мере
- •14. Применения комбинаторного анализа в теории вероятности
- •2. Основное комбинаторное правило (частный случай)
- •3. Основное комбинаторное правило (общий случай)
- •15. Постановка комбинаторной задачи
- •16. Выборка с возвращением и без возвращения
- •17. Выборки неупорядоченные и упорядоченные
- •18. Упорядоченные выборки с возвращением
- •19. Упорядоченные выборки без возвращения-размещения
- •20. Перестановки
- •21. Неупорядоченные выборки из n элементов по k без возвращения – сочетания
- •24.Употребление термина «случайный» в теории вероятностей
10. Необходимые в теории вероятностей сведения из теории множеств и теории меры
По существу, исходное определение теории вероятностей - определение вероятностного пространства в случае множества с конечным числом элементов в принципе уже дано.
Формулировка аксиом А.Н. Колмогорова или, что, то же самое, вероятностного пространства, требует привлечения понятий из теории множеств и теории меры.
Пусть
даны множества
 и
и
 .
.
Множество,
составленное из всех элементов
 ,
принадлежащих и
и
,
называют пересечением множеств
и
,
и обозначают через
,
принадлежащих и
и
,
называют пересечением множеств
и
,
и обозначают через
 или
или
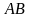 ,
их объединение
,
их объединение
 -
через
-
через
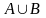 ,
разность
-
через
,
разность
-
через
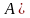 .
Через
.
Через
 обозначается пустое множество. Если
множества
и
не пересекаются
обозначается пустое множество. Если
множества
и
не пересекаются
 ,
то их объединение
будет обозначаться также через
,
то их объединение
будет обозначаться также через
 и называться суммой.
и называться суммой.
Тем
самым, операция вычитания
определена без ограничений для всяких
множеств
и
,
но в случае
 разность
разность
 носит специальное название дополнения
носит специальное название дополнения
 -
дополнения множества
до множества
.
-
дополнения множества
до множества
.
В
случае
разность
также называют дополнением
до
,
и обозначают
 .
В тех случаях, когда заранее оговорено,
что рассматриваемые множества есть
подмножества определенного множества
для данного множества
.
В тех случаях, когда заранее оговорено,
что рассматриваемые множества есть
подмножества определенного множества
для данного множества
 дополнение
до
также обозначают
дополнение
до
также обозначают
 (от
английского слова complement-
дополнение).
(от
английского слова complement-
дополнение).
Множество
 ,
элементами которого также являются
множества, называют системой
множеств.
,
элементами которого также являются
множества, называют системой
множеств.
Определение (алгебры множеств). Пусть - некоторое множество. Система А
подмножеств называется алгеброй, если
10.
 А
,
А
,
20.
 А
А
 А
А
30.
 А
А
 А
А
Приведенное определение является наиболее сжатым перечислением свойств системы множеств, в развернутом виде означающих следующее:
Система А подмножеств множества называется алгеброй, если А
объединение, пересечение и разность двух множеств системы опять принадлежат этой системе.
Действительно из свойств 20, 30 и теоретико-множественных равенств
 и
и

следует, что пересечение и разность множеств из А также принадлежит А.
Система множеств, составленное из всех подмножеств всякого множества , является алгеброй, поскольку множество есть подмножество самого себя и операции объединения, пересечения и вычитания, выполненные над подмножествами данного множества снова приводят к его подмножествам.
Функция, множество определения которой есть система множеств, называют функцией множеств.
Определение(конечно-аддитивной
вероятности). Пусть А-
алгебра
подмножеств конечного множества
.
Функция множеств
 ,
определенная на А,
принимающая значения в
,
определенная на А,
принимающая значения в
 ,
называется конечно-аддитивной,
если для любых двух непересекающихся
множеств
и
из А
,
называется конечно-аддитивной,
если для любых двух непересекающихся
множеств
и
из А
 (1)
(1)
В
случае
 ,
конечно-аддитивная функция множеств
,
конечно-аддитивная функция множеств
 называется конечно-аддитивной
вероятностной мерой, конечно- аддитивной
вероятностью или, коротко, вероятностью(но
в случае конечного множества
).
называется конечно-аддитивной
вероятностной мерой, конечно- аддитивной
вероятностью или, коротко, вероятностью(но
в случае конечного множества
).
Теперь мы в состоянии определить вероятностное пространство.
3. Основное определение
(Система аксиом Колмогорова вероятностного пространства в случае конечного множества ). Упорядоченный набор (тройка) объектов
,
где
10. - конечное множество произвольной природы;
20. А- алгебра всех подмножеств ;
30.
 -вероятность:
заданная на А
конечно-аддитивная неотрицательная
функция множеств, такая, что
-вероятность:
заданная на А
конечно-аддитивная неотрицательная
функция множеств, такая, что
 ,
,
называется
вероятностной моделью или вероятностным
пространством. При этом
называется пространством исходов или
пространством элементарных событий,
каждый элемент
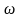 множества
-
элементарным событием, каждое множество
из алгебры А-
событием, а
множества
-
элементарным событием, каждое множество
из алгебры А-
событием, а
 -вероятностью
события
.
-вероятностью
события
.
Система аксиом I-III непротиворечива (существует хотя бы одна реализация).
Это
показывает следующий пример:
состоит из единственного элемента
,
А-
из
и пустого множества
,
при этом положено
,
 .
.
Система аксиом I-III, однако, не является полной (можно ещё добавить аксиомы так, чтобы оставалась непротиворечивой): в разных вопросах теории вероятностей рассматриваются различные вероятностные пространства, в их числе и с бесконечным .
