18. Упорядоченные выборки с возвращением

Имеется урна, в которой ровно n разных шаров. В силу возобновляемости урны, объем выборки k ничем не ограничен. Поэтому в качестве k берется натуральное число, без каких-либо ограничений.

Спрашивается, сколько будет всевозможных выборок объема k ? Чтобы получить ответ на поставленный вопрос, применим основное комбинаторное правило.

Выборку с возвращением объема k можем представить как процесс последовательного, одно за другим, в k действий, извлечения шаров из урны возобновляемого содержания из n шаров. В силу возобновляемости урны, каждое из k действий выполнимо n способами – по числу шаров в урне, и потому .

Тем самым, процесс извлечения шара выборки с номером a₁ осуществляется n способами.

Процесс извлечения шара той же выборки с номером a₂ осуществляется, в силу возобновляемости содержания урны, также n способами.

И, наконец, процесс извлечения последнего шара выборки с номером a_k осуществляется n способами.

Тем самым, согласно основному комбинаторному правилу, всего выборок (a₁,…a_k) будет .

Сам процесс образования выборки показывает, что это выборки с возвращением, и, одновременно, выборки упорядоченные.

В итоге, доказано, что

Из генеральной совокупности объема n извлекаются n^k всевозможных упорядоченных выборок с возвращением объема к.

19. Упорядоченные выборки без возвращения-размещения

Имеется урна, в которой ровно n разных шаров. Поскольку из невознобновляемой урны нельзя извлечь больше шаров, чем в ней содержится, то число извлекаемых шаров не больше n.

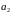В составляемой комбинации шар можно выбрать n способами, после чего в урне осталось (n-1) шаров, поэтому второй шар можно выбрать (n-1) способами. Продолжая этот процесс, получаем, что на последнем k-ом шаге в урне останется n-(k-1)=n-k+1 шаров, поэтому, в

силу основного комбинаторного правила, число всевозможных комбинаций будет (n-0)(n-1)…(n-(k-1))=n(n-1)…(n-k+1).

Другими словами, отвлекаясь от вспомогательной урновой схемы, в общем случае получаем, что в выборке элемент

выбирается n-0=n способами,

выбирается (n-1) способами,

и, отсюда замечая, что при всех элемент выбирается n-(m-1) способами, в частности, заключаем, что последний элемент выборки

- выбирается n-(k-1)=n-k+1 способами,

поэтому всего способов будет .

Тем самым, нами решена следующая конкретизация общей комбинаторной задачи:

Даны натуральные числа n и k, причем . Сколько из генеральной совокупности (множества) объема n можно извлечь упорядоченных выборок без возвращения объема k?

Ответ: произведению из k множителей, каждое из которых есть разность между n и числами 0,1,…, k-1: .

Упорядоченные выборки без возвращения также называют размещениями. Число размещений из n элементов по k обозначают . Таким образом,

= n(n-1)…(n-k+1).

20. Перестановки

Размещения из п по п называют перестановками, поскольку все такие выборки состоят из п разных элементов и отличаются друг от друга только порядком элементов. Число перестановок из п элементов обозначают . Так как по определению = , то сначала вычислим . Это есть произведение последовательных натуральных чисел от 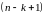при т. е. от 1 до п: Поэтому и =

Таким образом,

Для каждого натурального числа п число всевозможных перестановок генеральной совокупности объема п равно .