1.6 Этапы разработки алгоритма

1. Анализ условия задачи.

2. Составление математической модели.

3. На основе математической модели составляют блок-схему алгоритма.

4. Составление алгоритма на алгоритмическом языке и (или) языке программирования.

5. Формальное исполнение алгоритма.

Вопросы для самопроверки:

1. Какие стадии разработки алгоритма вы знаете и в чем их суть?

2. Приведите пример разработки алгоритма по стадиям.

3. Всегда ли результат выполнения одного и того же алгоритма одинаков?

2 Линейные алгоритмы

2.1 Понятие линейного алгоритма

Определение: Линейным называется алгоритм, в котором все этапы решения задачи выполняются строго последовательно, без пропусков и повторений.

Задача 1. Вычислить площадь прямоугольника S. Известно, что его ширина равна а, а длина в 2 раза больше ширины.

Решение.

1. Анализ условия задачи.

Площадь можно найти, перемножив длины сторон. Длина одной стороны известна – ширина а, задаваемая пользователем. Вторую сторону легко найти, зная, что она в 2 раза больше ширины.

Итак, проанализировав условие задачи, делаем вывод, что исходными данными (аргументом), является ширина а прямоугольника, а выходными данными являются длина (вторая сторона) и площадь. Причем вторая сторона – назовем ее b – это промежуточный результат, а площадь – назовем ее S – это искомый результат.

Все эти три объекта являются переменными, поскольку их значения станут известны в процессе выполнения алгоритма: первое будет задано пользователем, а два других будут получены в результате вычислений. Необходимо учесть, что все три переменные это вещественные числа.

2. Составим математическую модель решения нашей задачи. Запишем условие в виде одного предложения – найти площадь прямоугольника.

Наша задача может быть разбита на три основных этапа: ввод исходных данных, этап вычислений и вывод результатов. На первом этапе задается ширина а, на последнем этапе выводится результат – значение площади S.

Этап вычислений детализируем. Сначала вычисляется длина второй стороны – это первая подзадача. Затем, перемножив длины обеих сторон, получим значение площади – искомый результат – это вторая подзадача.

Таким образом, решение данной задачи состоит из двух действий. Используя введенные обозначения, запишем их:

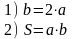
3. Учитывая все выше сказанное, составим блок-схему алгоритма нашей задачи. Она будет выглядеть как на рисунке 1.

4. Запишем алгоритм на алгоритмическом языке.

алг площадь прямоугольника

арг ВЕЩ а

рез ВЕЩ b, S

нач

ввод а

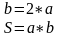
вывод S

кон

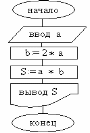
Рис. 1

2.2 Операторы целочисленного деления div и mod

Во многих языках программирования используют операции, применяемые только для переменных целого типа данных. Это оператор div, позволяющий вычислить целую часть от деления, и оператор mod, позволяющий вычислить остаток от деления. Например, 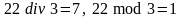, 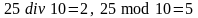. Чаще всего эти операции применяют в задачах о нахождении цифр целого числа.

Задача 2. Дано двузначное число. Найти сумму его цифр.

1. Анализ условия задачи. Дано одно двузначное число. Очевидно, что оно относится к классу целых чисел. Для того чтобы найти сумму цифр, сначала необходимо определить значения каждой цифры данного числа. Итак, делаем вывод, что аргументом является значение самого числа (назовем его Х), промежуточным результатом будут значения цифр этого числа (назовем число десятков А, число единиц В), окончательным результатом будет сумма цифр (назовем ее S).

Все эти объекты являются переменными, поскольку их значения станут известны в процессе выполнения алгоритма: первое будет задано пользователем, а другие будут получены в результате вычислений. Необходимо учесть, что все переменные это целые числа.

2. Составим математическую модель решения нашей задачи. Запишем условие в виде одного предложения – найти сумму цифр двузначного числа. Как и в задаче 10.1 эта задача также может быть разбита на три основных этапа: ввод исходных данных, этап вычислений и вывод результатов.

Детализируем этап вычислений. Понятно, что для получения результата, надо найти значения а) числа единиц; б) числа десятков; в) сумму значений, полученных в пунктах а) и б). Число единиц А найдем, используя операцию вычисления остатка от деления на 10, а число десятков В – с помощью операции вычисления целой части от деления на 10. Очевидно, что сумма S цифр вычисляется простым сложением А и В.

Решение состоит из трех действий. Используя введенные обозначения, запишем их:

.

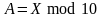
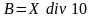
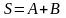3. Составим блок-схему алгоритма нашей задачи. Она будет выглядеть как на рисунке 2.

4

алг сумма цифр

арг ЦЕЛ Х

рез ЦЕЛ А, В, S

нач

ввод Х

вывод S

кон

. Запишем алгоритм на алгоритмическом языке.

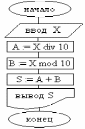
Рис. 2

Алгоритмический язык, также как и любой язык программирования, обладает определенным набором правил, с помощью которых записываются сложные по конструкции выражения.

Правила записи сложных выражений:

1. Аргументы функции записываются в круглых скобках.

2. Знак умножения обязательно прописывается с помощью символа «*». Например, выражение 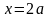на алгоритмическом языке следует записывать как .

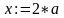3. Операция деления обозначается с помощью символа «/».

4. Обыкновенная дробь записывается в одну строку. Не допускается запись вида 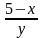. Подобные выражения записываются следующим образом: .

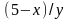5. При наличии в одном выражении нескольких операций они будут выполняться в порядке их приоритета (старшинства).

Пример: Выражение 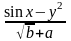следует записывать как:

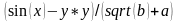
Вопросы для самопроверки:

1. Объясните назначение оператора div.

2. Объясните назначение оператора mod.

3. Дайте определение линейного алгоритма.

4. Опишите структуру записи алгоритма на алгоритмическом языке.

Вопросы для размышления:

1. В чем состоит отличие между операторами div, mod и «/»?

2. Что нужно использовать, чтобы изменить приоритет выполнения математических операций?

3. Как называются алгоритмы, в основе которых лежит структура «следование»?

4. Приведите примеры линейных алгоритмов.

Задания

1. Запишите на алгоритмическом языке выражения:

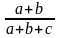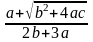
   а) ;	г)	ж) ;
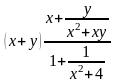   б) 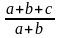;	д) 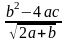;	з) ;
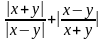   в) 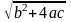;	е) 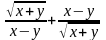;	и) .

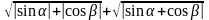2. Запишите на математическом языке выражения, записанные на алгоритмическом языке:

а) a/b*(c+d)-(a-b)/d/c+1;

б) x1+cos(y2-alfa)/2*abs(x4-ln(5)*y5)/sin(x2);

в) (p+q)/(r+s)-p*q/(r*s);

г) (sin(pi*alfa)*sin(pi*alfa))/cos(sqr(beta));

д) a^4/b*sqrt(c+d)-(a-b^3)/sqrt(b).

3. Вычислите значение выражения:

а) 113 div 7;	г) 238 div 17 - 238 mod 14;
б) 113 mod 7;	д) 222 div 2 mod 3;
в) 201 div 5 + 201 mod 11;	е) 1363 mod 11 div 3 + 2798 mod 28 div 9.

4. Разработайте алгоритм (по всем этапам) для решения следующих задач:

а) Вычислить площадь поверхности и объем куба со стороной, равной а.

б) Найдите площадь треугольника со сторонами a, b, c.

в) Дано трехзначное число а. Получить среднее арифметическое его цифр.

г) Написать последовательность для получения числа b, полученного выписыванием в обратном порядке цифр числа а. Если, например, дано число а = 1234, то должно получиться b = 4321.