
- •Лабораторная работа № 9 изучение электронного осциллографа
- •Краткая теория
- •1.1.Принцип работы осциллографа
- •1.2. Электронно-лучевая трубка
- •1.3. Принцип получения осциллограмм
- •1.4. Генератор пилообразного напряжения (генератор развертки)
- •Методика эксперимента Общий вид установки
- •2.1. Осциллограф-частотомер
- •Задание к лабораторной работе №9.
Методика эксперимента Общий вид установки

2.1. Осциллограф-частотомер
а)
Определить частоты синусоидального
напряжения можно с помощью фигур Лиссажу.
Для этого исследуемый сигнал подается
на одну пару пластин “У”, а на другую
пару пластин подается напряжение от
звукового генератора. Если частоты
будут относиться как целые числа
(например 1/1, 2/3, 4/5, и т.д.), то изображение
получится неподвижным. Подбирая частоту
звукового генератора можно добиться
такого положения, чтобы фигура Лиссажу
была развернутой (рис.6). При этом ![]() ;
; ![]() ;
; ![]() ,
т.е. линии не сливаются как при
,
т.е. линии не сливаются как при ![]() .
.
Тогда,
если мысленно заключить ее в квадрат и
посчитать число касаний к вертикальной
стороне квадрата и к горизонтальной
стороне квадрата, то соотношение этих
чисел будет равно отношению частот: ![]()
Р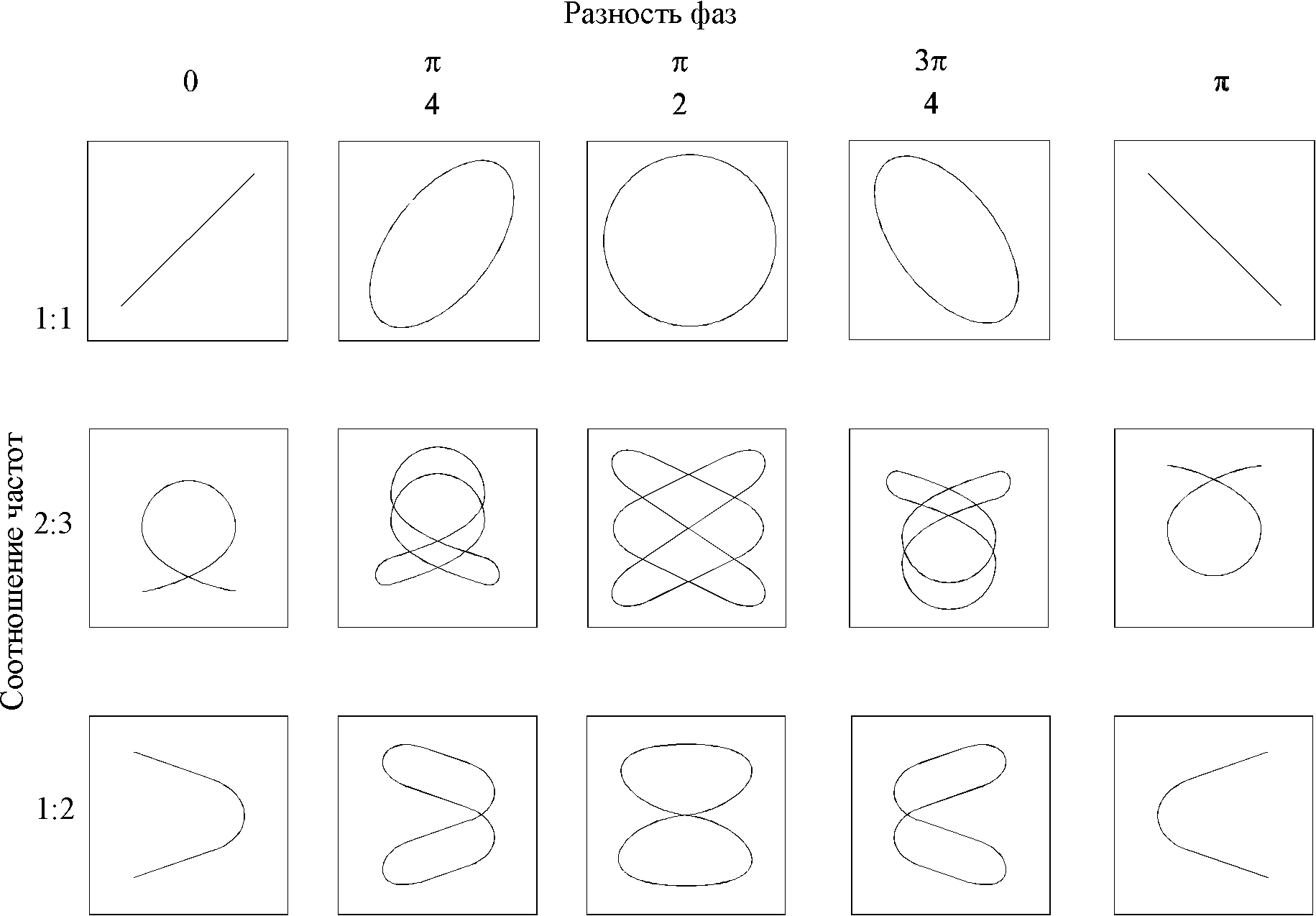 ис.6
ис.6
Это
легко понять из следующих рассуждений:
пусть период через который ситуация
будет повторяться, т.е. луч начнет
двигаться по прежней траектории будет
(рис.7). За это время напряжение Ux трижды
достигало максимума, т.е. число касаний
к вертикальной стороне квадрата будет
равно трем nx=3,
Uy максимума,
т.е. число касаний к горизонтальной
стороне квадрата будет равно двум ny=2.
Таким образом: ![]()
Р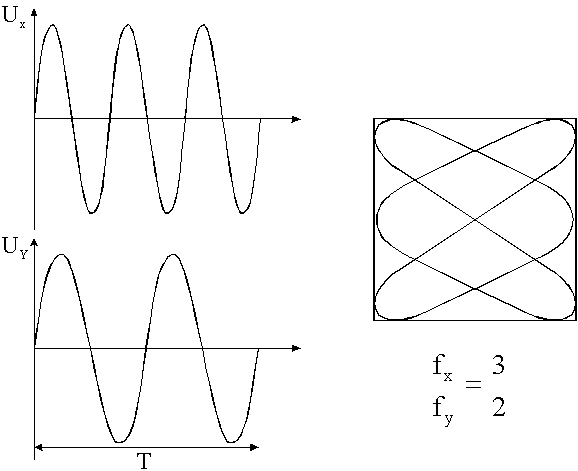 ис.7
ис.7
Определить частоту периодических сигналов любой формы можно используя непрерывную развертку. Для этого необходимо на вертикально отклоняющие пластины подать исследуемый сигнал, а на горизонтально отклоняющие пластины напряжение с генератора развертки и подобрать такую частоту пилообразного напряжения, чтобы на экране получилась осциллограмма (1-2 периода). Для того, чтобы она стала неподвижной, нужно подобрать уровень синхронизации. В современных осциллографах имеется переключатель строго калиброванной частоты генератора развертки. Поскольку время движения луча по горизонтали точно равно периоду пилообразного напряжения, ось Х можно проградуировать в единицах времени. Используя масштаб “время-деление”, указанный на переключателе частоты генератора развертки, измеряют период исследуемого сигнала.
Задание к лабораторной работе №9.
Упражнение 1.
Рассмотреть на осциллографе сигналы с генератора Л31 (прямоугольные, треугольные и синусоидальные импульсы). Измерить период сигналов на разных диапазонах частот осциллографом и сравнить его с показаниями генератора Л31.
Результаты занести в таблицу 1.
Таблица 1.
Вид импульса |
|
|
|
|
|
|
|
Упражнение 2.
Осциллограф-фазометр.
Фаза характеризует состояние гармонического
процесса в определенный момент времени.
Фазой гармонического колебания ![]() считают
аргумент
считают
аргумент ![]() .
Здесь U0 –
амплитуда колебаний,
.
Здесь U0 –
амплитуда колебаний, ![]() –
круговая частота, равная
–
круговая частота, равная ![]() ,
t –
время,
,
t –
время, ![]() –
начальная фаза характеризующая состояние
гармонического колебания в момент
начала отсчета времени, т.е. при t=0.
Из понятия фазы вытекает понятие о
сдвиге фаз двух гармонических колебаний
одной и той же частоты:
–
начальная фаза характеризующая состояние
гармонического колебания в момент
начала отсчета времени, т.е. при t=0.
Из понятия фазы вытекает понятие о
сдвиге фаз двух гармонических колебаний
одной и той же частоты:
![]() (1)
(1)
Сдвиг
фаз можно определить методом эллипса.
Если на пластины “Х” подано напряжение ![]() ,
а на пластины “У” – напряжение той же
частоты
,
а на пластины “У” – напряжение той же
частоты ![]() ,
то на экране осциллографа получится
изображение эллипса в виде:
,
то на экране осциллографа получится
изображение эллипса в виде:
![]() (2)
(2)
г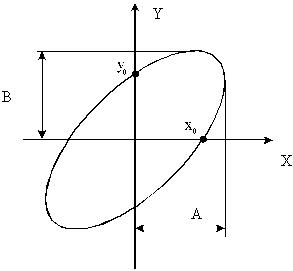 де
А и В – амплитудные, а Х и У – мгновенные
значения отклонения пятна в горизонтальном
и вертикальном направлениях соответственно
(рис.1).
де
А и В – амплитудные, а Х и У – мгновенные
значения отклонения пятна в горизонтальном
и вертикальном направлениях соответственно
(рис.1).
Рис.1 Результат сложения двух гармонических колебаний одинаковой частоты во взаимно перпендикулярных направлениях – эллипс.
Для определения точки пересечения этого эллипса с осями координат положим сначала у=0, а потом х=0. Тогда получим:
![]() (3)
(3)
Если отрегулировать усиление по “Х” и по “У” так, чтобы A=B=D, то получим, что
![]() (4)
(4)
Т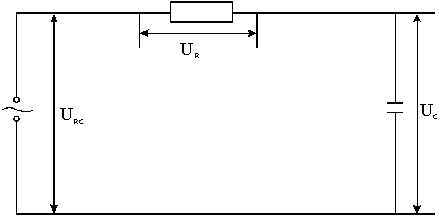 аким
образом, по точкам пересечения эллипса
с осями координат х0 и
у0 и
максимальному отклонению луча А и В
определяют сдвиг фаз между двумя
колебаниями одинаковой частоты.
аким
образом, по точкам пересечения эллипса
с осями координат х0 и
у0 и
максимальному отклонению луча А и В
определяют сдвиг фаз между двумя
колебаниями одинаковой частоты.
Рис.2 Последовательная RC-цепочка
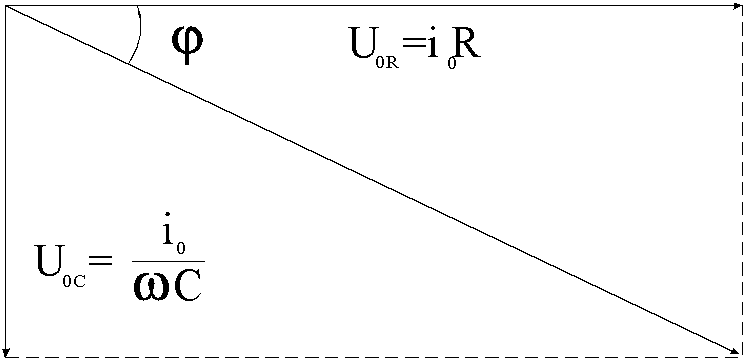
Рис.3 Векторная диаграмма напряжений на RC-цепочке.
Два
напряжения, сдвинутые по фазе, можно
получить с помощью последовательной RC-цепочки
(рис.2), состоящей из активного
сопротивления R и
емкости С. Напряжение на емкости U0C всегда
отстает по фазе от напряжения на
сопротивлении U0R на
,
как показано на условной векторной
диаграмме (рис.3), где вектор ![]() соответствует
амплитудному значению напряжения на
емкости, а вектор
соответствует
амплитудному значению напряжения на
емкости, а вектор ![]() –
амплитудному значению напряжения на
сопротивлении. Известно, что амплитудное
значение напряжения на емкости:
–
амплитудному значению напряжения на
сопротивлении. Известно, что амплитудное
значение напряжения на емкости:
![]() (5)
(5)
Где С – емкость, – круговая частота, io – амплитудное значение тока.
Таким
образом, суммарное амплитудное напряжение
на RC-цепочке
равно векторной сумме ![]() ,
т.е.:
,
т.е.:
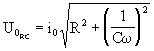 (6)
(6)
Очевидно,
это напряжение отстает от напряжения
на сопротивлении U0R=iR0 на
угол ![]() .
Этот фазовый сдвиг определяется
соотношением:
.
Этот фазовый сдвиг определяется
соотношением:
![]() (7)
(7)
ЗАДАНИЕ.2
1. Составить схему.
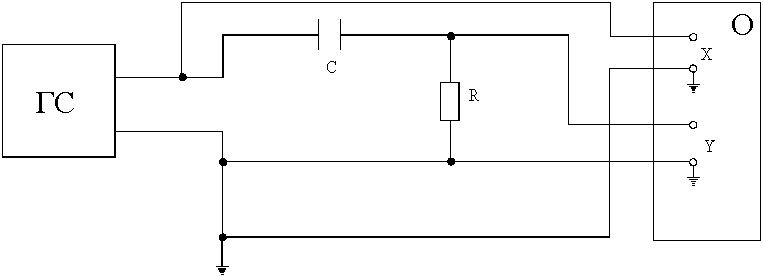
Рис.4 схема для изучения сдвига фаз между током и напряжением на RC-цепочке. ГС – генератор сигналов синусоидальной формы, С – магазин емкостей, R – магазин сопротивлений, О – осциллограф.
На пластины “Х” подать напряжение от генератора, а на пластины “У” – напряжение пропорциональное току, с активного сопротивления R. На экране осциллографа получается изображение эллипса.
Увеличивая R, С и , убедится в том, что сдвиг фаз между напряжением на активном сопротивлении R и генераторе URC уменьшается (эллипс превращается в прямую), а при уменьшении R, С и – увеличивается, приближаясь к (наклон у эллипса исчезает, а при одинаковых напряжениях Uox и Uoy эллипс превращается в окружность).
Зафиксировать любые два параметра R и С, С и или
и R и в зависимости от изменения третьего параметра измерить сдвиг фаз 5-6 раз используя формулы (3) и (4). Сравнить полученные значения сдвига фаз с расчетными по формуле (7). Результаты представить в таблице 2.
Таблица 2.
R |
С |
f |
|
|
|
|
|
|
|
|
|
|
|
Упражнение 3.
Интегрирующие и дифференцирующие цепочки. RC-цепочка, представленная на рис.4, может быть использована для преобразования формы сигналов путем интегрирования и дифференцирования импульсов.
Рассмотрим дифференциальные уравнения для такой цепочки. Пусть на RC-цепочку (рис.5) подано напряжение U=f(t). По закону Кирхгофа:
![]() (8)
(8)
Где
, q –
заряд на конденсаторе в момент времени t.
По определению ток ![]() ,
поэтому уравнение (8) можно записать
иначе
,
поэтому уравнение (8) можно записать
иначе
![]() (9)
(9)
Р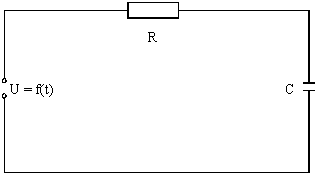 ис.5 RC-цепочка.
ис.5 RC-цепочка.
Подберем R и
С таким образом, чтобы ![]() ,
т.е. сопротивление R было
бы
,
т.е. сопротивление R было
бы ![]() .
В этом случае в уравнении (9) можно
пренебречь вторым членом, то есть:
.
В этом случае в уравнении (9) можно
пренебречь вторым членом, то есть:
![]() (10)
(10)
Теперь найдем, чему будет равно падение напряжения на емкости UC, если согласно (10) i=U/R:
![]() (11)
(11)
В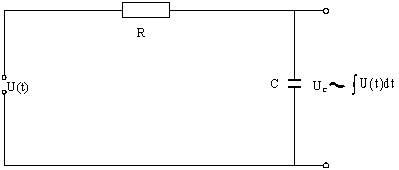 идно,
что напряжение на емкости UC прямо
пропорционально интегралу от напряжения
на всей RC-цепочке.
Такая цепочка называется интегрирующей
(рис.6).
идно,
что напряжение на емкости UC прямо
пропорционально интегралу от напряжения
на всей RC-цепочке.
Такая цепочка называется интегрирующей
(рис.6).
Рис.6 Интегрирующая RC-цепочка.
Теперь рассмотрим обратное соотношение, т.е. подберем R и С так, чтобы RC>>R, и рассчитаем, чему в этом случае равно напряжение на активном сопротивлении R. В этом случае в уравнении (8) можно пренебречь падением напряжения на сопротивлении R и оно приобретает вид:
![]() (12)
(12)
После дифференцирования уравнения (12) получим:
![]() (13)
(13)
Значит напряжение на активном сопротивлении:
![]() (14)
(14)
Т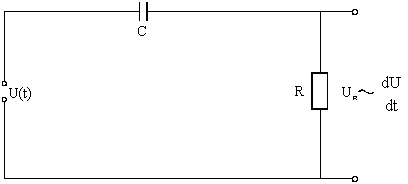 аким
образом, напряжение на
сопротивлении R пропорционально
производной от суммарного напряжения
на RC-цепочке.
Такая цепочка называется дифференцирующей.
аким
образом, напряжение на
сопротивлении R пропорционально
производной от суммарного напряжения
на RC-цепочке.
Такая цепочка называется дифференцирующей.
Рис.7 Дифференцирующая RC-цепочка.
ЗАДАНИЕ
Составить интегрирующую цепочку (рис.8). В качестве входного сигнала U взять генератор импульсов Л31, а для исследования выходного сигнала UC осциллограф С1-83. Подать входной и выходной сигналы на 1 и 2 каналы осциллографа, включить генератор развертки осциллографа и пронаблюдать оба сигнала в зависимости от времени t. Подобрать соотношение R и С так, чтобы
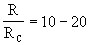
. Затем измеряя параметры f, R и С, получить проинтегрированные сигналы от прямоугольных и треугольных импульсов. Результаты занести в таблицу 3.
Р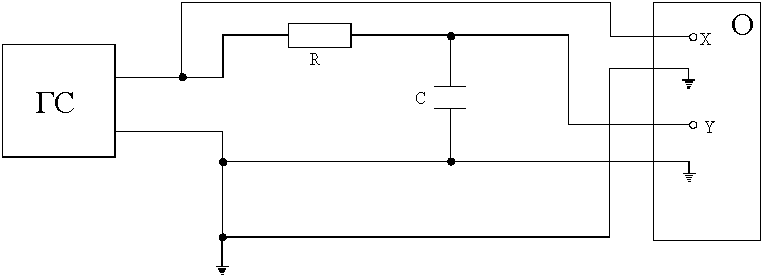 ис.8
Схема для исследования проинтегрированных
сигналов.
ис.8
Схема для исследования проинтегрированных
сигналов.
Составить дифференцирующую цепочку (рис.7 или 4). Подобрать R и С так, чтобы

. Изменяя параметры f, R и С, получить продифференцированные импульсы от прямоугольных и треугольных импульсов в зависимости от времени. Результаты занести в таблицу 3.
Таблица 3.
Вид входного и выходного сигналов |
f |
R |
C |
|
Интегрирование импульсов |
||||
|
|
|
|
|
Дифференцирование импульсов |
||||
|
|
|
|
|
